Algoritmus: Rozdiel medzi revíziami
| (27 medziľahlých úprav od 3 ďalších používateľov nie je zobrazených) | |||
| Riadok 2: | Riadok 2: | ||
[[Kategória:Informatika]] | [[Kategória:Informatika]] | ||
{{Skripta_ZI}} | {{Skripta_ZI}} | ||
| − | + | __TOC__ | |
==<big>Algoritmus</big>== | ==<big>Algoritmus</big>== | ||
'''Algoritmus''' znamená proces alebo súbor pravidiel ktoré sa majú dodržiavať pri operáciach alebo riešení problémov. Algoritmus sa preto týka súboru pravidiel,pokynov ktoré postupne definujú, ako sa má práca vykonať, aby sa dosiahli očakávané výsledky.<ref>>https://www.geeksforgeeks.org/introduction-to-algorithms/</ref> | '''Algoritmus''' znamená proces alebo súbor pravidiel ktoré sa majú dodržiavať pri operáciach alebo riešení problémov. Algoritmus sa preto týka súboru pravidiel,pokynov ktoré postupne definujú, ako sa má práca vykonať, aby sa dosiahli očakávané výsledky.<ref>>https://www.geeksforgeeks.org/introduction-to-algorithms/</ref> | ||
| + | |||
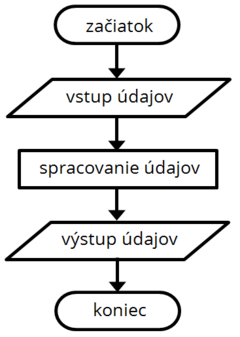
| + | Práca počítača je presne determinovaná. Počítač je absolútne neiniciatívny a všetko, čo chceme, aby urobil mu musíme nariadiť. Prácu počítaču nariaďujeme programom. K tomu aby sme mohli program zostaviť potrebujeme vytvoriť postupnosť krokov, ktorá v každom okamihu určuje ako postupovať ďalej, tzv. algoritmus. Jedna z definícií algoritmu hovorí, že algoritmus je presný popis definujúci výpočtový proces, vedúci od meniteľných vstupných údajov až k žiadaným výsledkom. Táto definícia síce presne vystihuje podstatu a účel algoritmu, je však úzko špecializovaná Obmedzuje sa len na výpočtový proces. Algoritmy však nepoužívame len pri počítačoch pri príprave programov, ale ich použitie je všeobecné. Pomocou algoritmu totiž môžeme presne definovať akýkoľvek determinovaný proces. | ||
| + | |||
[[Súbor:Univerzalny algoritmus.png|none|240px|]] | [[Súbor:Univerzalny algoritmus.png|none|240px|]] | ||
| Riadok 13: | Riadok 16: | ||
==<big>Vlasnosti algoritmu</big>== | ==<big>Vlasnosti algoritmu</big>== | ||
| − | + | ===Hlavné vlasnosti algoritmu=== | |
| − | + | ;Jasný a jednoznačný: Každý krok algoritmu musí byť presne definovaný a nesmie dovoľovať viacej výkladov, teda nesmie pripúšťať pochybnosť o tom, ako postupovať ďalej - t. j. ako jednotlivé kroky nasledujú po sebe, | |
| + | |||
| + | ;Všeobecnosť: Algoritmus musí vyhovovať riešeniu všeobecnej skupiny úloh. Algoritmus musí vychádzať s meniteľných vstupných údajov, t. j. musí to byť popis riešenia nie len jednej úlohy, ale celej skupiny príbuzných úloh líšiacich sa od seba len vstupnými údajmi, <ref>https://spseke.sk/tutor/projekt/algoritmy.htm</ref>. Ako príklad môžeme uviesť riešenie kvadratickej rovnice, kde menitenými vstupnými údajmi sú koeficienty a,b,c a skupina úloh toho istého typu je množina všetkých kvadratických rovníc, kde a,b,c patria do R. | ||
| + | |||
| + | ;Rezultatívnosť: Algoritmus musí vždy vyústiť do nejakého riešenia a to po konečnom počte krokov. Podotknime, že výsledok algoritmu môže byť aj "neviem" alebo "riešenie neexistuje", čo sa dá považovať správny výsledok. | ||
| + | ;Konečnosť: Počet opakovaní každého kroku je konečný | ||
| − | + | ;Elementárnosť: Algoritmus pozostáva z konečného počtu elementárnych krokov. | |
| − | Algoritmus | ||
| − | |||
| − | + | ===Doplnkové vlasnosti alogritmu=== | |
| − | |||
| + | ;Zrozumiteľnosť: Použitie takých prostriedkov na zápis algoritmu, ktoré by mali byť zrozumiteľné rôznym pracovníkom, ktorí budú s algoritmom pracovať (analytik, programátor, používateľ, oponent...). | ||
| − | + | ;Správnosť: Algoritmus musí úplne a správne riešiť danú úlohu. | |
| − | |||
| − | |||
| + | ;Efektívnosť: Algoritmus má byť čo najvýhodnejší (najefektívnejší). Zmyslom efektívnosti je minimalizovať nároky na spracovanie činnosti podľa algoritmu. Efektívnosť môžeme posudzovať z rôznych hľadísk (výpočtový čas a kapacita pamätí počítača, minimalizácia finančných nárokov, minimalizácia spotreby energie, minimalizácia nárokov na personálne alebo materiálne vybavenie, minimalizácia dopadov na životné prostredie a pod.), prípadne sa snažíme optimalizovať vzájomný vzťah viacerých hľadísk. Táto požiadavka je často v rozpore s požiadavkou na štruktúrovanosť (prehľadnosť, modulárnosť, usporiadanosť) algoritmu. | ||
| − | + | ;Modifikovateľnosť: Algoritmus by mal byť vytvorený tak, aby sa dal ľahko modifikovať pri potrebnej zmene vyvolanej zmenou podmienok riešenia (vonkajších a vnútorných). | |
| − | Algoritmus | ||
| − | |||
| + | ;Štruktúrovanosť: Požiadavka na vnútornú štruktúru algoritmu, ktorý by mal byť rozdelený na relatívne samostatné, ale logicky nadväzujúce celky, ktoré riešia vždy príslušnú časť algoritmu, požiadavka súvisí so zrozumiteľnosťou a modifikovateľnosťou, dobre štruktúrovaný algoritmus je zrozumiteľný a ľahko modifikovateľný (opraviteľný). | ||
==Riešenie problému pomocou algorimtu== | ==Riešenie problému pomocou algorimtu== | ||
| Riadok 48: | Riadok 52: | ||
==Značky vývojových diagramov== | ==Značky vývojových diagramov== | ||
| − | [[Súbor: | + | [[Súbor:začiatok.png|100px|none]] Značka sa využíva na začatie alebo ukončenie vývojového diagramu |
| + | |||
| − | |||
| − | [[Súbor: | + | [[Súbor:Untitled Diagram.png|100px|none]] Výkonný blok na program |
| − | |||
| − | |||
| − | + | [[Súbor:Vstuo.png|100px|none]] Služi na zápis vstup a výstupov vývojoveého diagramu | |
| − | + | ||
| + | |||
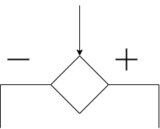
| − | [[Súbor: | + | [[Súbor:Untitled Diagram (3).png|160px|none]] Rozhodovací blok s jedným vstupom a viacerými výstupmi |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[Súbor:Spojka.png|none|30px]] Spojka | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | [[Súbor:Spojnica.png|none|160px]] Spojnica | |
| − | |||
| − | |||
| − | + | ==Príklady== | |
| − | + | '''Príklady''' na tvorbu vývojových diagramov nájdete v sekcií: | |
| − | + | [http://www.kiwiki.info/index.php/Jazyk_C_(príklady)_-_Algoritmy[Príklady algoritmus]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | = | + | =Referencie= |
<references/> | <references/> | ||
Aktuálna revízia z 21:54, 19. september 2022
Učebné texty
Obsah
Algoritmus
Algoritmus znamená proces alebo súbor pravidiel ktoré sa majú dodržiavať pri operáciach alebo riešení problémov. Algoritmus sa preto týka súboru pravidiel,pokynov ktoré postupne definujú, ako sa má práca vykonať, aby sa dosiahli očakávané výsledky.[1]
Práca počítača je presne determinovaná. Počítač je absolútne neiniciatívny a všetko, čo chceme, aby urobil mu musíme nariadiť. Prácu počítaču nariaďujeme programom. K tomu aby sme mohli program zostaviť potrebujeme vytvoriť postupnosť krokov, ktorá v každom okamihu určuje ako postupovať ďalej, tzv. algoritmus. Jedna z definícií algoritmu hovorí, že algoritmus je presný popis definujúci výpočtový proces, vedúci od meniteľných vstupných údajov až k žiadaným výsledkom. Táto definícia síce presne vystihuje podstatu a účel algoritmu, je však úzko špecializovaná Obmedzuje sa len na výpočtový proces. Algoritmy však nepoužívame len pri počítačoch pri príprave programov, ale ich použitie je všeobecné. Pomocou algoritmu totiž môžeme presne definovať akýkoľvek determinovaný proces.
Navrhnutý algoritmus je nezávislý od jazyka, tzn. že ide iba o jednoduché pokyny, ktoré je možné implementovať v akomkoľvek jazyku, a napriek tomu bude výstup rovnaký, ako sa očakávalo.
Vlasnosti algoritmu
Hlavné vlasnosti algoritmu
- Jasný a jednoznačný
- Každý krok algoritmu musí byť presne definovaný a nesmie dovoľovať viacej výkladov, teda nesmie pripúšťať pochybnosť o tom, ako postupovať ďalej - t. j. ako jednotlivé kroky nasledujú po sebe,
- Všeobecnosť
- Algoritmus musí vyhovovať riešeniu všeobecnej skupiny úloh. Algoritmus musí vychádzať s meniteľných vstupných údajov, t. j. musí to byť popis riešenia nie len jednej úlohy, ale celej skupiny príbuzných úloh líšiacich sa od seba len vstupnými údajmi, [2]. Ako príklad môžeme uviesť riešenie kvadratickej rovnice, kde menitenými vstupnými údajmi sú koeficienty a,b,c a skupina úloh toho istého typu je množina všetkých kvadratických rovníc, kde a,b,c patria do R.
- Rezultatívnosť
- Algoritmus musí vždy vyústiť do nejakého riešenia a to po konečnom počte krokov. Podotknime, že výsledok algoritmu môže byť aj "neviem" alebo "riešenie neexistuje", čo sa dá považovať správny výsledok.
- Konečnosť
- Počet opakovaní každého kroku je konečný
- Elementárnosť
- Algoritmus pozostáva z konečného počtu elementárnych krokov.
Doplnkové vlasnosti alogritmu
- Zrozumiteľnosť
- Použitie takých prostriedkov na zápis algoritmu, ktoré by mali byť zrozumiteľné rôznym pracovníkom, ktorí budú s algoritmom pracovať (analytik, programátor, používateľ, oponent...).
- Správnosť
- Algoritmus musí úplne a správne riešiť danú úlohu.
- Efektívnosť
- Algoritmus má byť čo najvýhodnejší (najefektívnejší). Zmyslom efektívnosti je minimalizovať nároky na spracovanie činnosti podľa algoritmu. Efektívnosť môžeme posudzovať z rôznych hľadísk (výpočtový čas a kapacita pamätí počítača, minimalizácia finančných nárokov, minimalizácia spotreby energie, minimalizácia nárokov na personálne alebo materiálne vybavenie, minimalizácia dopadov na životné prostredie a pod.), prípadne sa snažíme optimalizovať vzájomný vzťah viacerých hľadísk. Táto požiadavka je často v rozpore s požiadavkou na štruktúrovanosť (prehľadnosť, modulárnosť, usporiadanosť) algoritmu.
- Modifikovateľnosť
- Algoritmus by mal byť vytvorený tak, aby sa dal ľahko modifikovať pri potrebnej zmene vyvolanej zmenou podmienok riešenia (vonkajších a vnútorných).
- Štruktúrovanosť
- Požiadavka na vnútornú štruktúru algoritmu, ktorý by mal byť rozdelený na relatívne samostatné, ale logicky nadväzujúce celky, ktoré riešia vždy príslušnú časť algoritmu, požiadavka súvisí so zrozumiteľnosťou a modifikovateľnosťou, dobre štruktúrovaný algoritmus je zrozumiteľný a ľahko modifikovateľný (opraviteľný).
Riešenie problému pomocou algorimtu
1. Problém, ktorý má tento algoritmus vyriešiť.
2. Obmedzenia problému, ktoré je potrebné zohľadniť pri jeho riešení.
3. Vstup, ktorý sa má prijať na vyriešenie problému.
4. Výstup, ktorý možno očakávať, keď sa problém vyrieši.
5. Riešenie tohto problému v daných obmedzeniach.[3]
Značky vývojových diagramov
Značka sa využíva na začatie alebo ukončenie vývojového diagramu
Výkonný blok na program
Služi na zápis vstup a výstupov vývojoveého diagramu
Rozhodovací blok s jedným vstupom a viacerými výstupmi
Spojka
Spojnica
Príklady
Príklady na tvorbu vývojových diagramov nájdete v sekcií: [Príklady algoritmus]