Triedenie zlučovaním: Rozdiel medzi revíziami
| (36 medziľahlých úprav od 2 ďalších používateľov nie je zobrazených) | |||
| Riadok 3: | Riadok 3: | ||
{{Skripta programovanie}} | {{Skripta programovanie}} | ||
__TOC__ | __TOC__ | ||
| − | |||
| − | ==Zlučovací algoritmus Merge== | + | ==Merge Sort== |
| − | [[Súbor:Funkcia merge.png|500px|náhľad|vpravo|Vizualizácia funkcie Merge: Máme pole prvkov ''p = [1, 3, 5, 2, 4, 6]'', ktoré je už čiastočne utriedené. Použijeme algoritmus Merge, ktorý si vytvorí pomocné polia ''L = [1, 3, 5]'' a ''P = [2, 4, 6]''. Všetky polia indexujeme od ''0'', pričom pre pole ''p'' používame index ''k'', pre ''L'' index ''i'' a pre ''P'' index ''j''. Postupnosť krokov je označená číslicami 1 až 6. | + | |
| + | ===Zlučovací algoritmus Merge=== | ||
| + | [[Súbor:Funkcia merge.png|500px|náhľad|vpravo|Vizualizácia funkcie ''Merge'': Máme pole prvkov ''p = [1, 3, 5, 2, 4, 6]'', ktoré je už čiastočne utriedené. Použijeme algoritmus ''Merge'', ktorý si vytvorí pomocné polia ''L = [1, 3, 5]'' a ''P = [2, 4, 6]''. Všetky polia indexujeme od ''0'', pričom pre pole ''p'' používame index ''k'', pre ''L'' index ''i'' a pre ''P'' index ''j''. Postupnosť krokov je označená číslicami 1 až 6. | ||
]] | ]] | ||
| − | Princíp zlučovania tkvie v tom, že máme dva alebo viac utriedených zoznamov, ktoré | + | Princíp zlučovania tkvie v tom, že máme dva alebo viac utriedených zoznamov, ktoré skombinujeme do jedného utriedeného zoznamu (výsledný zoznam musí obsahovať všetky prvky z pôvodných zoznamov). Zoznam môže byť reprezentovaný ako dátová štruktúra pole alebo aj ako lineárny zoznam. V tomto článku sa zameriame na algoritmus pre dátovú štruktúru pole. |
| − | Algoritmus Merge tvorí kľúčovú časť triediaceho algoritmu | + | Algoritmus ''Merge'' tvorí kľúčovú časť triediaceho algoritmu ''Merge Sort''. |
| − | = | + | ====Vlastnosti algoritmu==== |
| − | |||
| − | |||
| − | ===Vlastnosti algoritmu=== | ||
* vhodný pre dátové štruktúry: pole, lineárny zoznam | * vhodný pre dátové štruktúry: pole, lineárny zoznam | ||
* časová náročnosť: vždy lineárna <math>O(n)</math> | * časová náročnosť: vždy lineárna <math>O(n)</math> | ||
* priestorová náročnosť: lineárna <math>O(n)</math> pre pole (alokovanie pomocných polí), <math>O(1)</math> pre lineárny zoznam (pri lineárnom zozname netreba alokovať dočasné polia, stačí iba presmerovať smerníky) | * priestorová náročnosť: lineárna <math>O(n)</math> pre pole (alokovanie pomocných polí), <math>O(1)</math> pre lineárny zoznam (pri lineárnom zozname netreba alokovať dočasné polia, stačí iba presmerovať smerníky) | ||
| − | * využitie: kľúčový podprogram pre triediaci algoritmus | + | * využitie: kľúčový podprogram pre triediaci algoritmus ''Merge Sort'' |
| + | |||
| + | ====Základné časti algoritmu==== | ||
| + | # Vytvorenie pomocných polí. | ||
| + | # Prechádzanie pomocných polí a vyberanie minima z 2 prvkov. | ||
| + | # Vkladanie minima na začiatok výsledného poľa. | ||
| + | # Kopírovanie prvkov, ktoré ešte neboli porovnané, z pomocného poľa do výsledného poľa. | ||
| + | |||
| + | ====Slovný opis algoritmu==== | ||
| + | Nech máme vstupné pole, ktoré sa skladá z dvoch už utriedených polovíc. Vytvoríme si dve pomocné polia ''L'' a ''P'' a do každého z nich skopírujeme obsah jednej polovice (''L'' - ľavá polovica, ''P'' - pravá polovica). Potom súčasne prechádzame polia ''L'' a ''P'' od začiatku po koniec, pričom v každej iterácii porovnáme prvok poľa ''L'' s prvkom v poli ''P''. Z tejto dvojice následne vyberieme minimum, (keď triedime od najmenšieho po najväčší) ktoré vložíme na prvú voľnú pozíciu pôvodného poľa (na začiatku je to prvá pozícia poľa). Nakoniec zvýšime index pri vstupnom poli a pri pomocnom poli, z ktorého vyberáme daný prvok. Túto postupnosť krokov opakujeme, pokiaľ neprídeme na koniec jedného z polí ''P'' a ''L''. Ak nastane situácia, že prídeme na koniec jedného z pomocných polí (a v druhom nám ostali ešte nejaké prvky), potom už iba naspäť skopírujeme zbytok druhého pomocného poľa na koniec pôvodného poľa. | ||
| − | ===Pseudokód=== | + | ====Pseudokód==== |
| − | Nech funkcia Merge má nasledovný prototyp: <code>Merge(pole[], lavy, stred, pravy)</code> | + | Nech funkcia ''Merge'' má nasledovný prototyp: <code>Merge(pole[], lavy, stred, pravy)</code> |
:1. Je <code>lavy >= pravy ? Ak áno, skonči, inak pokračuj krokom 2.</code> | :1. Je <code>lavy >= pravy ? Ak áno, skonči, inak pokračuj krokom 2.</code> | ||
:2. Nech: <code>i = 0, j = 0, k = lavy </code> | :2. Nech: <code>i = 0, j = 0, k = lavy </code> | ||
| Riadok 51: | Riadok 58: | ||
:::7.4. Skoč na krok 7. | :::7.4. Skoč na krok 7. | ||
| − | ==Merge | + | ===Merge Sort=== |
| − | Merge Sort je triediaci algoritmus, ktorý využíva stratégiu '''"rozdeľuj a panuj"''', čo znamená, že vstupný zoznam najskôr rozdelí na | + | ''Merge Sort'' je triediaci algoritmus, ktorý využíva stratégiu '''"rozdeľuj a panuj"''', čo znamená, že vstupný zoznam najskôr rozdelí na menšie časti, tie zoradí a potom ich zlúči naspäť dokopy. Radí sa medzi najpoužívanejšie a najviac rešpektované triediace algoritmy. |
| − | ===Vlastnosti algoritmu Merge Sort=== | + | ====Vlastnosti algoritmu Merge Sort==== |
* vhodný pre dátové štruktúry: pole, lineárny zoznam | * vhodný pre dátové štruktúry: pole, lineárny zoznam | ||
* časová náročnosť: vždy linearitmická <math> O(n.log(n)) </math>, vďaka ktorej dokáže efektívne triediť veľmi veľké zoznamy | * časová náročnosť: vždy linearitmická <math> O(n.log(n)) </math>, vďaka ktorej dokáže efektívne triediť veľmi veľké zoznamy | ||
| − | * priestorová náročnosť: lineárna <math>O(n)</math> pre pole (alokovanie dočasných polí), konštantná <math>O(1)</math> pre lineárny zoznam (pri | + | * priestorová náročnosť: lineárna <math>O(n)</math> pre pole (alokovanie dočasných polí), konštantná <math>O(1)</math> pre lineárny zoznam (pri lineárnom zozname stačí iba presmerovať smerníky) |
* druh triedenia: triedenie zlučovaním (komparačný algoritmus) | * druh triedenia: triedenie zlučovaním (komparačný algoritmus) | ||
* stabilita triedenia: stabilný | * stabilita triedenia: stabilný | ||
* miesto triedenia: externé triedenie (vhodný na triedenie veľkých objemov dát uložených na disku) | * miesto triedenia: externé triedenie (vhodný na triedenie veľkých objemov dát uložených na disku) | ||
| − | Z hľadiska implementácie môžeme vytvoriť dve základné verzie algoritmu, a to rekurzívnu a iteračnú. | + | Z hľadiska implementácie môžeme vytvoriť dve základné verzie algoritmu, a to ''rekurzívnu'' a ''iteračnú''. |
| − | ===Opis rekurzívnej a iteračnej verzie algoritmu Merge Sort=== | + | |
| + | ====Opis rekurzívnej a iteračnej verzie algoritmu Merge Sort==== | ||
<tabs> | <tabs> | ||
<tab name="Rekurzívna verzia" block> | <tab name="Rekurzívna verzia" block> | ||
| − | [[Súbor:Merge sort.png|400px|náhľad|vpravo|Vizualizácia rekurzívnej verzie algoritmu | + | [[Súbor:Merge sort.png|400px|náhľad|vpravo|Vizualizácia rekurzívnej verzie algoritmu Merge Sort: chronologický priebeh algoritmu je znázornený číslicami 1 až 19.]] |
| − | === | + | ====Základné časti algoritmu==== |
| − | |||
# Delenie poľa na dve polovice. | # Delenie poľa na dve polovice. | ||
# Triedenie ľavej polovice poľa. | # Triedenie ľavej polovice poľa. | ||
# Triedenie pravej polovice poľa. | # Triedenie pravej polovice poľa. | ||
| − | # Zlúčenie oboch polovíc pomocou funkcie Merge. | + | # Zlúčenie oboch polovíc pomocou funkcie ''Merge''. |
| − | ===Slovný opis=== | + | ====Slovný opis==== |
| − | Našou úlohou je vzostupne (min - max) utriediť vstupné pole. Určíme si stred poľa (pri párnom počte prvkov je to ten menší z prostredných indexov). Následne vykonávame sériu rekurzívnych delení pre ľavú a pravú časť poľa (začiatok ... stred ; stred + 1 ... koniec) až do momentu, keď nám ostanú len jednoprvkové podpolia (tie sú už utriedené). Následne v každom volaní obe tieto podpolia zlúčime pomocou algoritmu Merge do väčších podpolí (2, 4, 8, ...), až nakoniec dostaneme jedno výsledné utriedené pole. | + | Našou úlohou je vzostupne (min -> max) utriediť vstupné pole. Určíme si stred poľa (pri párnom počte prvkov je to ten menší z prostredných indexov). Následne vykonávame sériu rekurzívnych delení pre ľavú a pravú časť poľa (''začiatok ... stred ; stred + 1 ... koniec'') až do momentu, keď nám ostanú len jednoprvkové podpolia (tie sú už utriedené). Následne v každom volaní obe tieto podpolia zlúčime pomocou algoritmu ''Merge'' do väčších podpolí (max: 2, 4, 8, ...), až nakoniec dostaneme jedno výsledné utriedené pole. |
| − | ===Pseudokód=== | + | ====Pseudokód==== |
| − | Nech | + | Nech má funkcia ''MergeSort'' nasledovný prototyp: <code>MergeSort(pole[], lavy, pravy) </code> |
:1. Je <code>lavy >= pravy</code> ? Ak áno, skonči volanie, inak pokračuj krokom 2. | :1. Je <code>lavy >= pravy</code> ? Ak áno, skonči volanie, inak pokračuj krokom 2. | ||
:2. Nech: <code>stred = lavy + (pravy - lavy) / 2</code>, pričom znak ''/'' vyjadruje celočíselné delenie. | :2. Nech: <code>stred = lavy + (pravy - lavy) / 2</code>, pričom znak ''/'' vyjadruje celočíselné delenie. | ||
| Riadok 88: | Riadok 95: | ||
:4. Zavolaj funkciu <code>Merge(pole[], lavy, stred, pravy)</code> | :4. Zavolaj funkciu <code>Merge(pole[], lavy, stred, pravy)</code> | ||
:5. Skonči volanie. | :5. Skonči volanie. | ||
| + | |||
| + | |||
| Riadok 96: | Riadok 105: | ||
</tab> | </tab> | ||
<tab name="Iteračná verzia" block> | <tab name="Iteračná verzia" block> | ||
| − | [[Súbor:MergeSort IT.png|400px|náhľad|vpravo]] | + | [[Súbor:MergeSort IT.png|400px|náhľad|Vizualizácia iteračnej verzie algoritmu Merge Sort: chronologický priebeh algoritmu je znázornený číslicami 1 až 7.|vpravo]] |
| − | === | + | ====Základné časti algoritmu==== |
| − | + | # Určenie maximálnej veľkosti podpoľa na zlučovanie. | |
| − | # | + | # Prechádzanie jednotlivých podpolí v poli. |
| − | # | + | # Zlučovanie jednotlivých podpolí pomocou funkcie ''Merge''. |
| − | # Zlučovanie jednotlivých | ||
| − | ===Slovný opis=== | + | ====Slovný opis==== |
| − | Vstupné pole, ktoré má ''N'' prvkov, môžeme chápať, ako ''N'' rôznych jednoprvkových (utriedených) podpolí, ktoré máme zlúčiť do jedného výsledného ''N''-prvkového utriedeného poľa. Keďže by bolo veľmi nepraktické zlučovať ''N'' podpolí naraz, zvolíme nasledovnú stratégiu: Budeme prechádzať dané pole od začiatku po koniec a v | + | Vstupné pole, ktoré má ''N'' prvkov, môžeme chápať, ako ''N'' rôznych jednoprvkových (utriedených) podpolí, ktoré máme zlúčiť do jedného výsledného ''N'' - prvkového utriedeného poľa. Keďže by bolo veľmi nepraktické zlučovať ''N'' podpolí naraz, zvolíme nasledovnú stratégiu: Budeme prechádzať dané pole od začiatku po koniec a v prvej iterácii zlúčime každé dva prvky, čím dostaneme <math>\frac{N}{2}</math> dvojprvkových utriedených podpolí. Potom v druhej iterácii zlúčime každé 4 prvky do jedného podpoľa, v treťom cykle každých 8, ..., až do momentu, keď dostaneme jedno výsledné utriedené pole. |
| − | Aby sme | + | Aby sme mohli túto stratégiu implementovať, potrebujeme dva cykly: vonkajší, ktorý nastaví maximálnu veľkosť podpoľa, ktoré ideme zlučovať (1,2,4,8 ... ''dlzka - 1'') a vnútorný, ktorý prechádza jednotlivé podpolia. Následne už iba voláme funkciu ''Merge'', ktorá dané podpolia zlučuje. |
| − | Poznámka, ak máme pole, ktoré má nepárny počet prvkov, tak ten posledný prvok nezlúčime hneď v | + | Poznámka, ak máme ''pole'', ktoré má nepárny počet prvkov, tak ten posledný prvok nezlúčime hneď v prvej iterácii, ale až v tých ďalších. Takisto, ak ''N'' nie je mocnina čísla 2, tak musíme samozrejme ošetriť situáciu, kedy by sme sa dostali mimo rozsah poľa (Ak máme napríklad ''pole'', čo má 7 prvkov, tak po prvej iterácii budú prvky utiredené podľa vzoru 2 + 2 + 2 + 1, po druhej 4 + 3, a po tretej 7 + 0) |
| − | ===Pseudokód=== | + | ====Pseudokód==== |
| − | Nech nech má funkcia MergeSort nasledovný prototyp: <code>MergeSort(pole[], lavy, pravy) </code> | + | Nech nech má funkcia ''MergeSort'' nasledovný prototyp: <code>MergeSort(pole[], lavy, pravy) </code> |
:1. Je <code>lavy >= pravy</code> ? Ak áno, skonči, inak pokračuj krokom 2. | :1. Je <code>lavy >= pravy</code> ? Ak áno, skonči, inak pokračuj krokom 2. | ||
| − | :2. Nech: <code> | + | :2. Nech: <code>dlzka_podpola = 1 </code> |
:3. Nech: <code>zaciatok = lavy</code> | :3. Nech: <code>zaciatok = lavy</code> | ||
| − | :4. Je<code> | + | :4. Je <code>dlzka_podpola <= pravy</code> ? Ak áno pokračuj krokom 4.1, inak skonči. |
| − | :::4.1. Je<code>zaciatok < pravy</code> Ak áno pokračuj krokom 4.1.1, inak skoč na krok 4.2. | + | :::4.1. Je <code>zaciatok < pravy</code> Ak áno pokračuj krokom 4.1.1, inak skoč na krok 4.2. |
:::::4.1.1. Je <code>zaciatok + 2 * dlzka_zoznamu - 1 <= pravy</code> ? | :::::4.1.1. Je <code>zaciatok + 2 * dlzka_zoznamu - 1 <= pravy</code> ? | ||
:::::::Ak áno: | :::::::Ak áno: | ||
| − | :::::::::4.1.1.1. Nech <code>koniec = zaciatok + 2 * | + | :::::::::4.1.1.1. Nech: <code>koniec = zaciatok + 2 * dlzka_podpola - 1</code> |
:::::::Ak nie: | :::::::Ak nie: | ||
| − | :::::::::4.1.1.1. Nech <code>koniec = pravy</code> | + | :::::::::4.1.1.1. Nech: <code>koniec = pravy</code> |
| − | :::::4.1.2. Je <code>zaciatok + | + | :::::4.1.2. Je <code>zaciatok + dlzka_podpola - 1 <= pravy</code> ? |
:::::::Ak áno: | :::::::Ak áno: | ||
| − | :::::::::4.1.2.1. Nech <code>stred = zaciatok + | + | :::::::::4.1.2.1. Nech <code>stred = zaciatok + dlzka_podpola - 1</code> |
:::::::Ak nie: | :::::::Ak nie: | ||
:::::::::4.1.2.1. Nech <code>stred = pravy</code> | :::::::::4.1.2.1. Nech <code>stred = pravy</code> | ||
:::::4.1.3. <code>Merge(pole[], zaciatok, stred, koniec)</code> | :::::4.1.3. <code>Merge(pole[], zaciatok, stred, koniec)</code> | ||
| − | :::::4.1.4. <code>zaciatok += 2 * | + | :::::4.1.4. <code>zaciatok += 2 * dlzka_podpola</code> |
:::::4.1.5. Skoč na krok 4.1. | :::::4.1.5. Skoč na krok 4.1. | ||
| − | :::4.2. <code> | + | :::4.2. <code>dlzka_podpole *= 2</code> |
| − | :::4.3 Skoč na krok 4. | + | :::4.3. Skoč na krok 4. |
</tab> | </tab> | ||
</tabs> | </tabs> | ||
| − | ==Implementácia algoritmov Merge a MergeSort | + | ===Implementácia algoritmov Merge a MergeSort v rôznych programovacích jazykoch=== |
<tabs> | <tabs> | ||
<tab name="Rekurzívna: C " block> | <tab name="Rekurzívna: C " block> | ||
| Riadok 390: | Riadok 398: | ||
int stred, koniec; | int stred, koniec; | ||
| − | for (int | + | for (int dlzka_podpola = 1; dlzka_podpola <= pravy; dlzka_podpola *= 2) |
{ | { | ||
| − | for (int zaciatok = lavy; zaciatok < pravy ; zaciatok += 2 * | + | for (int zaciatok = lavy; zaciatok < pravy; zaciatok += 2 * dlzka_podpola) |
{ | { | ||
| − | + | koniec = (zaciatok + 2 * dlzka_podpola - 1 <= pravy) ? zaciatok + 2 * dlzka_podpola - 1 : pravy; | |
| − | + | stred = (zaciatok + dlzka_podpola - 1 <= pravy) ? zaciatok + dlzka_podpola - 1 : pravy; | |
| − | + | Merge(pole, zaciatok, stred, koniec); | |
} | } | ||
} | } | ||
} | } | ||
| − | |||
</syntaxhighlight> | </syntaxhighlight> | ||
</tab> | </tab> | ||
| Riadok 552: | Riadok 559: | ||
void Merge(int pole[], int lavy, int stred, int pravy); | void Merge(int pole[], int lavy, int stred, int pravy); | ||
| − | void | + | void MergeSortIt(int *pole, int lavy, int pravy); |
/* hlavný program */ | /* hlavný program */ | ||
| Riadok 568: | Riadok 575: | ||
} | } | ||
| − | + | MergeSortIt(pole, 0, dlzka_pola - 1); | |
cout<<endl<<"Utriedené pole:"<<endl; | cout<<endl<<"Utriedené pole:"<<endl; | ||
| Riadok 653: | Riadok 660: | ||
} | } | ||
| − | void | + | void MergeSortIt(int *pole, int lavy, int pravy) |
{ | { | ||
/* ak má pole menej ako 2 prvky, skonči volanie */ | /* ak má pole menej ako 2 prvky, skonči volanie */ | ||
| Riadok 664: | Riadok 671: | ||
int stred, koniec; | int stred, koniec; | ||
| − | for (int | + | for (int dlzka_podpola = 1; dlzka_podpola <= pravy; dlzka_podpola *= 2) |
{ | { | ||
| − | for (int zaciatok = lavy; zaciatok < pravy; zaciatok += 2 * | + | for (int zaciatok = lavy; zaciatok < pravy; zaciatok += 2 * dlzka_podpola) |
{ | { | ||
| − | koniec = (zaciatok + 2 * | + | koniec = (zaciatok + 2 * dlzka_podpola - 1 <= pravy) ? zaciatok + 2 * dlzka_podpola - 1 : pravy; |
| − | stred = (zaciatok + | + | stred = (zaciatok + dlzka_podpola - 1 <= pravy) ? zaciatok + dlzka_podpola - 1 : pravy; |
Merge(pole, zaciatok, stred, koniec); | Merge(pole, zaciatok, stred, koniec); | ||
| Riadok 686: | Riadok 693: | ||
/* Funkcia zlúči 2 podpolia, ktoré sme vytvorili z pôvodného poľa. | /* Funkcia zlúči 2 podpolia, ktoré sme vytvorili z pôvodného poľa. | ||
* Každé podpole má polovičnú dĺžku pôvodného poľa. | * Každé podpole má polovičnú dĺžku pôvodného poľa. | ||
| − | * | + | * podpole1 [ľavý ... stred] |
| − | * | + | * podpole2 [stred + 1 ... pravý] |
| + | */ | ||
void merge(int[] pole, int lavy, int stred, int pravy) | void merge(int[] pole, int lavy, int stred, int pravy) | ||
| Riadok 735: | Riadok 743: | ||
} | } | ||
| − | /* V prípade, že sa v jednom zo | + | /* V prípade, že sa v jednom zo podpolí nachádzajú ešte nejaké prvky, ktoré neboli zlúčené do poľa, |
| − | * tak sa do | + | * tak sa do poľa jednoducho skopírujú |
| + | */ | ||
while (i < n1) | while (i < n1) | ||
| Riadok 760: | Riadok 769: | ||
if (lavy < pravy) | if (lavy < pravy) | ||
{ | { | ||
| − | // Musíme nájsť stred | + | // Musíme nájsť stred poľa |
int stred = lavy + (pravy - lavy) / 2; | int stred = lavy + (pravy - lavy) / 2; | ||
| − | // Zoradíme prvú a druhú polovicu | + | // Zoradíme prvú a druhú polovicu poľa samostatne |
sort(pole, lavy, stred); | sort(pole, lavy, stred); | ||
sort(pole, stred + 1, pravy); | sort(pole, stred + 1, pravy); | ||
| − | // Zlúčime zoradené polovice do jedného | + | // Zlúčime zoradené polovice do jedného poľa |
merge(pole, lavy, stred, pravy); | merge(pole, lavy, stred, pravy); | ||
| Riadok 778: | Riadok 787: | ||
public class Main | public class Main | ||
{ | { | ||
| − | /* Funkcia na výpis | + | /* Funkcia na výpis poľa dĺžky n */ |
static void vypis_pole(int[] pole) | static void vypis_pole(int[] pole) | ||
| Riadok 812: | Riadok 821: | ||
<tab name="Iteračná: Java" block> | <tab name="Iteračná: Java" block> | ||
<syntaxhighlight lang="Java"> | <syntaxhighlight lang="Java"> | ||
| − | class MergeSort_iteracia { | + | class MergeSort_iteracia |
| − | /* Zlúči 2 | + | { |
| − | * Každé | + | /* Zlúči 2 podpolia, ktoré sa vytvorili z pôvodného poľa. |
| − | * | + | * Každé podpole má polovičnú dĺžku pôvodného poľa. |
| − | * | + | * podpole1 [ľavý..stred] |
| − | void merge(int[] pole, int lavy, int stred, int pravy) { | + | * podpole2 [stred+1..pravý] |
| − | // Výpočet dĺžky 2 | + | */ |
| + | |||
| + | void merge(int[] pole, int lavy, int stred, int pravy) | ||
| + | { | ||
| + | // Výpočet dĺžky 2 podpolí | ||
| + | |||
int n1 = stred - lavy + 1; | int n1 = stred - lavy + 1; | ||
int n2 = pravy - stred; | int n2 = pravy - stred; | ||
// Vytvorenie pomocných polí | // Vytvorenie pomocných polí | ||
| + | |||
int[] L = new int[n1]; | int[] L = new int[n1]; | ||
int[] P = new int[n2]; | int[] P = new int[n2]; | ||
// Načítanie dát do pomocných polí | // Načítanie dát do pomocných polí | ||
| + | |||
for (int i = 0; i < n1; i++) | for (int i = 0; i < n1; i++) | ||
L[i] = pole[lavy + i]; | L[i] = pole[lavy + i]; | ||
| Riadok 833: | Riadok 849: | ||
P[j] = pole[stred + 1 + j]; | P[j] = pole[stred + 1 + j]; | ||
| − | // Počiatočné indexy prvého a druhého | + | // Počiatočné indexy prvého a druhého podpoľa |
| + | |||
int i = 0, j = 0; | int i = 0, j = 0; | ||
| − | // Počiatočný index zlúčeného | + | |
| + | // Počiatočný index zlúčeného podpoľa | ||
| + | |||
int k = lavy; | int k = lavy; | ||
// Zlúčenie dvoch podpolí | // Zlúčenie dvoch podpolí | ||
| − | while (i < n1 && j < n2) { | + | |
| − | if (L[i] <= P[j]) { | + | while (i < n1 && j < n2) |
| + | { | ||
| + | if (L[i] <= P[j]) | ||
| + | { | ||
pole[k] = L[i]; | pole[k] = L[i]; | ||
i++; | i++; | ||
} | } | ||
| − | else { | + | else |
| + | { | ||
pole[k] = P[j]; | pole[k] = P[j]; | ||
j++; | j++; | ||
| Riadok 851: | Riadok 874: | ||
} | } | ||
| − | /* V prípade, že v jednom | + | /* V prípade, že v jednom z podpolí sa nachádzajú prvky, ktoré neboli zlúčené do poľa, |
| − | * tak sa do | + | * tak sa do poľa jednoducho skopírujú |
| − | while (i < n1) { | + | */ |
| + | |||
| + | while (i < n1) | ||
| + | { | ||
pole[k] = L[i]; | pole[k] = L[i]; | ||
i++; | i++; | ||
| Riadok 859: | Riadok 885: | ||
} | } | ||
| − | while (j < n2) { | + | while (j < n2) |
| + | { | ||
pole[k] = P[j]; | pole[k] = P[j]; | ||
k++; | k++; | ||
| Riadok 867: | Riadok 894: | ||
/* Funkcia, ktorá zoradí pole použitím funkcie merge() */ | /* Funkcia, ktorá zoradí pole použitím funkcie merge() */ | ||
| − | void sort (int[] pole, int n) { | + | |
| − | /* Dĺžka | + | void sort (int[] pole, int n) |
| + | { | ||
| + | /* Dĺžka podpolí, ktoré majú byť zlúčené, hodnoty premennej sa pohybujú v intervale <1;n-1> */ | ||
| + | |||
int aktual_dlzka; | int aktual_dlzka; | ||
| − | /* Začiatočný index ľavého | + | |
| + | /* Začiatočný index ľavého podpoľa, ktoré má byť zlúčené */ | ||
| + | |||
int zaciatok_vlavo; | int zaciatok_vlavo; | ||
| − | /* Vzostupné usporiadanie prvkov. Najskôr sa zlúčia | + | /* Vzostupné usporiadanie prvkov. Najskôr sa zlúčia podpolia veľkosti 1 do podpolí veľkosti 2, |
| − | * potom | + | * potom podpolia veľkosti 2 do podpolí veľkosti 4 a tak ďalej |
| − | for (aktual_dlzka = 1; aktual_dlzka <= n - 1; aktual_dlzka *= 2) { | + | */ |
| − | /* Určenie začiatočného prvku rôznych | + | |
| − | for (zaciatok_vlavo = 0; zaciatok_vlavo < n - 1; zaciatok_vlavo += 2 * aktual_dlzka) { | + | for (aktual_dlzka = 1; aktual_dlzka <= n - 1; aktual_dlzka *= 2) |
| − | /* Nájdenie konečného prvku ľavého | + | { |
| + | /* Určenie začiatočného prvku rôznych podpolí aktuálnej dĺžky podpoľa */ | ||
| + | |||
| + | for (zaciatok_vlavo = 0; zaciatok_vlavo < n - 1; zaciatok_vlavo += 2 * aktual_dlzka) | ||
| + | { | ||
| + | /* Nájdenie konečného prvku ľavého podpoľa, stred+1 je začiatočný prvok pravého podpoľa */ | ||
| + | |||
int stred = Math.min(zaciatok_vlavo + aktual_dlzka - 1, n - 1); | int stred = Math.min(zaciatok_vlavo + aktual_dlzka - 1, n - 1); | ||
int koniec_vpravo = Math.min(zaciatok_vlavo + 2 * aktual_dlzka - 1, n - 1); | int koniec_vpravo = Math.min(zaciatok_vlavo + 2 * aktual_dlzka - 1, n - 1); | ||
| − | /* Zlúči | + | /* Zlúči podpolia L[zaciatok_vlavo .. stred] & P[stred+1 .. koniec_vpravo] */ |
| + | |||
merge(pole, zaciatok_vlavo, stred, koniec_vpravo); | merge(pole, zaciatok_vlavo, stred, koniec_vpravo); | ||
} | } | ||
| Riadok 890: | Riadok 929: | ||
public class Main { | public class Main { | ||
| − | /* Funkcia na výpis | + | |
| − | static void vypis_pole(int[] pole) { | + | /* Funkcia na výpis poľa dĺžky n */ |
| + | |||
| + | static void vypis_pole(int[] pole) | ||
| + | { | ||
int n = pole.length; | int n = pole.length; | ||
| − | for (int j : pole) { | + | for (int j : pole) |
| + | { | ||
System.out.print(j + " "); | System.out.print(j + " "); | ||
} | } | ||
| Riadok 901: | Riadok 944: | ||
/* Hlavný program */ | /* Hlavný program */ | ||
| + | |||
public static void main(String[] args) { | public static void main(String[] args) { | ||
| − | /* Inicializácia | + | /* Inicializácia poľa */ |
| + | |||
int[] pole = {12, 11, 13, 5, 6, 7}; | int[] pole = {12, 11, 13, 5, 6, 7}; | ||
| Riadok 924: | Riadok 969: | ||
def MergeSort(pole): | def MergeSort(pole): | ||
if len(pole) > 1: | if len(pole) > 1: | ||
| − | # Nájdenie stredu | + | |
| − | # zápis len(pole)//2 znamená, že dĺžka | + | # Nájdenie stredu poľa |
| + | # zápis len(pole)//2 znamená, že dĺžka poľa sa vydelí 2 a výsledok je celé číslo | ||
| + | |||
stred = len(pole) // 2 | stred = len(pole) // 2 | ||
| − | # Rozdelenie | + | # Rozdelenie poľa na dve časti |
| + | |||
L = pole[:stred] | L = pole[:stred] | ||
P = pole[stred:] | P = pole[stred:] | ||
| − | # Zoradenie najskôr prvej časti | + | # Zoradenie najskôr prvej časti poľa, potom druhej |
| + | |||
MergeSort(L) | MergeSort(L) | ||
MergeSort(P) | MergeSort(P) | ||
| Riadok 938: | Riadok 987: | ||
i = j = k = 0 | i = j = k = 0 | ||
| − | # Zlúčenie a zoradenie údajov z pomocných polí do jedného | + | # Zlúčenie a zoradenie údajov z pomocných polí do jedného poľa |
| + | |||
while i < len(L) and j < len(P): | while i < len(L) and j < len(P): | ||
if L[i] < P[j]: | if L[i] < P[j]: | ||
| Riadok 949: | Riadok 999: | ||
# Kontrola či všetky prvky boli zlúčené dokopy, | # Kontrola či všetky prvky boli zlúčené dokopy, | ||
| − | # ak nie, tak sa do zlúčeného | + | # ak nie, tak sa do zlúčeného poľa jednoducho skopírujú |
| + | |||
while i < len(L): | while i < len(L): | ||
pole[k] = L[i] | pole[k] = L[i] | ||
| Riadok 962: | Riadok 1 013: | ||
# Hlavný program | # Hlavný program | ||
| + | |||
if __name__ == '__main__': | if __name__ == '__main__': | ||
| + | |||
pole = [12, 11, 13, 5, 6, 7] | pole = [12, 11, 13, 5, 6, 7] | ||
| Riadok 979: | Riadok 1 032: | ||
<syntaxhighlight lang="Python3"> | <syntaxhighlight lang="Python3"> | ||
def MergeSort_iteracia(pole): | def MergeSort_iteracia(pole): | ||
| − | # Dĺžka | + | |
| + | # Dĺžka podpolí, ktoré majú byť zlúčené, hodnoty premennej sa pohybujú v intervale <1;n-1> | ||
| + | |||
aktual_dlzka = 1 | aktual_dlzka = 1 | ||
| − | # Vonkajší cyklus, ktorý určuje | + | # Vonkajší cyklus, ktorý určuje podpolia aktuálnej dĺžky |
| + | |||
while aktual_dlzka < len(pole) - 1: | while aktual_dlzka < len(pole) - 1: | ||
| + | |||
lavy = 0 | lavy = 0 | ||
| − | # Vnútorný cyklus, ktorý slúži na zlúčenie a zoradenie | + | # Vnútorný cyklus, ktorý slúži na zlúčenie a zoradenie podpolí do jedného podpoľa |
| + | |||
while lavy < len(pole) - 1: | while lavy < len(pole) - 1: | ||
| − | # Index stredného prvku sa určí, keď k indexu ľavého prvku | + | |
| − | # dĺžku | + | # Index stredného prvku sa určí, keď k indexu ľavého prvku podpoľa pripočítame aktuálnu |
| + | # dĺžku podpolí a odčítame 1 | ||
| + | |||
stred = min((lavy + aktual_dlzka - 1), len(pole) - 1) | stred = min((lavy + aktual_dlzka - 1), len(pole) - 1) | ||
| − | # Ak platí podmienka 2 * aktuálna dĺžka < dĺžka | + | # Ak platí podmienka 2 * aktuálna dĺžka < dĺžka poľa - 1, tak pravý index = aktuálnej dĺžke subpolí, |
| − | # inak pravý index = | + | # inak pravý index = dĺžka poľa - 1 |
| + | |||
pravy = ((2 * aktual_dlzka + lavy - 1, len(pole) - 1)[2 * aktual_dlzka + lavy - 1 > len(pole) - 1]) | pravy = ((2 * aktual_dlzka + lavy - 1, len(pole) - 1)[2 * aktual_dlzka + lavy - 1 > len(pole) - 1]) | ||
# Volanie funkcie merge | # Volanie funkcie merge | ||
| + | |||
merge(pole, lavy, stred, pravy) | merge(pole, lavy, stred, pravy) | ||
| Riadok 1 002: | Riadok 1 064: | ||
# Aktuálna dĺžka sa sa zmení na dvojnásobok jej predošlej hodnoty | # Aktuálna dĺžka sa sa zmení na dvojnásobok jej predošlej hodnoty | ||
| + | |||
aktual_dlzka = 2 * aktual_dlzka | aktual_dlzka = 2 * aktual_dlzka | ||
def merge(pole, lavy, stred, pravy): | def merge(pole, lavy, stred, pravy): | ||
| + | |||
n1 = stred - lavy + 1 | n1 = stred - lavy + 1 | ||
n2 = pravy - stred | n2 = pravy - stred | ||
# Inicializácia pomocných polí | # Inicializácia pomocných polí | ||
| + | |||
L = [0] * n1 | L = [0] * n1 | ||
P = [0] * n2 | P = [0] * n2 | ||
# Načítanie dát do pomocných polí | # Načítanie dát do pomocných polí | ||
| + | |||
for i in range(0, n1): | for i in range(0, n1): | ||
L[i] = pole[lavy + i] | L[i] = pole[lavy + i] | ||
| Riadok 1 021: | Riadok 1 087: | ||
i, j, k = 0, 0, lavy | i, j, k = 0, 0, lavy | ||
| − | # Zlúčenie a zoradenie údajov z pomocných polí do jedného | + | # Zlúčenie a zoradenie údajov z pomocných polí do jedného poľa |
| + | |||
while i < n1 and j < n2: | while i < n1 and j < n2: | ||
if L[i] > P[j]: | if L[i] > P[j]: | ||
| Riadok 1 033: | Riadok 1 100: | ||
# Kontrola či všetky prvky boli zlúčené dokopy, | # Kontrola či všetky prvky boli zlúčené dokopy, | ||
# ak nie, tak sa do zlúčeného pola jednoducho skopírujú | # ak nie, tak sa do zlúčeného pola jednoducho skopírujú | ||
| + | |||
while i < n1: | while i < n1: | ||
pole[k] = L[i] | pole[k] = L[i] | ||
| Riadok 1 045: | Riadok 1 113: | ||
# Hlavný program | # Hlavný program | ||
| + | |||
if __name__ == '__main__': | if __name__ == '__main__': | ||
| + | |||
pole = [12, 11, 13, 5, 6, 7] | pole = [12, 11, 13, 5, 6, 7] | ||
Aktuálna revízia z 16:30, 19. apríl 2021
Obsah
Merge Sort
Zlučovací algoritmus Merge
Princíp zlučovania tkvie v tom, že máme dva alebo viac utriedených zoznamov, ktoré skombinujeme do jedného utriedeného zoznamu (výsledný zoznam musí obsahovať všetky prvky z pôvodných zoznamov). Zoznam môže byť reprezentovaný ako dátová štruktúra pole alebo aj ako lineárny zoznam. V tomto článku sa zameriame na algoritmus pre dátovú štruktúru pole.
Algoritmus Merge tvorí kľúčovú časť triediaceho algoritmu Merge Sort.
Vlastnosti algoritmu
- vhodný pre dátové štruktúry: pole, lineárny zoznam
- časová náročnosť: vždy lineárna [math]O(n)[/math]
- priestorová náročnosť: lineárna [math]O(n)[/math] pre pole (alokovanie pomocných polí), [math]O(1)[/math] pre lineárny zoznam (pri lineárnom zozname netreba alokovať dočasné polia, stačí iba presmerovať smerníky)
- využitie: kľúčový podprogram pre triediaci algoritmus Merge Sort
Základné časti algoritmu
- Vytvorenie pomocných polí.
- Prechádzanie pomocných polí a vyberanie minima z 2 prvkov.
- Vkladanie minima na začiatok výsledného poľa.
- Kopírovanie prvkov, ktoré ešte neboli porovnané, z pomocného poľa do výsledného poľa.
Slovný opis algoritmu
Nech máme vstupné pole, ktoré sa skladá z dvoch už utriedených polovíc. Vytvoríme si dve pomocné polia L a P a do každého z nich skopírujeme obsah jednej polovice (L - ľavá polovica, P - pravá polovica). Potom súčasne prechádzame polia L a P od začiatku po koniec, pričom v každej iterácii porovnáme prvok poľa L s prvkom v poli P. Z tejto dvojice následne vyberieme minimum, (keď triedime od najmenšieho po najväčší) ktoré vložíme na prvú voľnú pozíciu pôvodného poľa (na začiatku je to prvá pozícia poľa). Nakoniec zvýšime index pri vstupnom poli a pri pomocnom poli, z ktorého vyberáme daný prvok. Túto postupnosť krokov opakujeme, pokiaľ neprídeme na koniec jedného z polí P a L. Ak nastane situácia, že prídeme na koniec jedného z pomocných polí (a v druhom nám ostali ešte nejaké prvky), potom už iba naspäť skopírujeme zbytok druhého pomocného poľa na koniec pôvodného poľa.
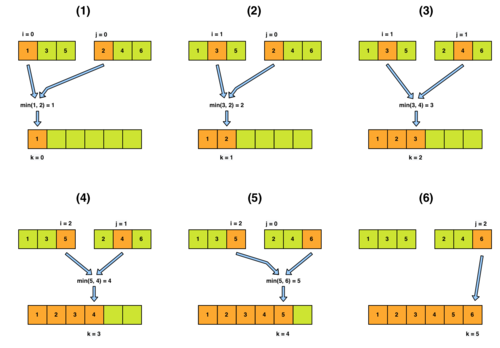
Pseudokód
Nech funkcia Merge má nasledovný prototyp: Merge(pole[], lavy, stred, pravy)
- 1. Je
lavy >= pravy ? Ak áno, skonči, inak pokračuj krokom 2. - 2. Nech:
i = 0, j = 0, k = lavy - 3. Nech:
dlzka_L = stred - lavy + 1, dlzka_P = pravy - stred - 4. Nech:
L = pole[lavy ... stred], P = pole[stred + 1 ... pravy] - 5. Je
i < dlzka_La zároveňj < dlzka_P? Ak áno, pokračuj krokom 5.1., inak skoč na krok 6.- 5.1. Je
L[i] <= P[j]?- Ak áno:
- 5.1.1.
pole[k] = L[i] - 5.1.2.
k += 1 - 5.1.3.
i += 1 - 5.1.4. Skoč na krok 5.
- 5.1.1.
- Ak nie:
- 5.1.1.
pole[k] = P[j] - 5.1.2.
k += 1 - 5.1.3.
j += 1 - 5.1.4. Skoč na krok 5.
- 5.1.1.
- Ak áno:
- 5.1. Je
- 6. Je
i < dlzka_L? Ak áno, pokračuj krokom 6.1., inak skoč na krok 7.- 6.1.
pole[k] = L[i] - 6.2.
k += 1 - 6.3.
i += 1 - 6.4. Skoč na krok 6.
- 6.1.
- 7. Je
j < dlzka_P? Ak áno, pokračuj krokom 7.1., inak skonči.- 7.1.
pole[k] = P[j] - 7.2.
k += 1 - 7.3.
j += 1 - 7.4. Skoč na krok 7.
- 7.1.
Merge Sort
Merge Sort je triediaci algoritmus, ktorý využíva stratégiu "rozdeľuj a panuj", čo znamená, že vstupný zoznam najskôr rozdelí na menšie časti, tie zoradí a potom ich zlúči naspäť dokopy. Radí sa medzi najpoužívanejšie a najviac rešpektované triediace algoritmy.
Vlastnosti algoritmu Merge Sort
- vhodný pre dátové štruktúry: pole, lineárny zoznam
- časová náročnosť: vždy linearitmická [math] O(n.log(n)) [/math], vďaka ktorej dokáže efektívne triediť veľmi veľké zoznamy
- priestorová náročnosť: lineárna [math]O(n)[/math] pre pole (alokovanie dočasných polí), konštantná [math]O(1)[/math] pre lineárny zoznam (pri lineárnom zozname stačí iba presmerovať smerníky)
- druh triedenia: triedenie zlučovaním (komparačný algoritmus)
- stabilita triedenia: stabilný
- miesto triedenia: externé triedenie (vhodný na triedenie veľkých objemov dát uložených na disku)
Z hľadiska implementácie môžeme vytvoriť dve základné verzie algoritmu, a to rekurzívnu a iteračnú.
Opis rekurzívnej a iteračnej verzie algoritmu Merge Sort
Základné časti algoritmu
- Delenie poľa na dve polovice.
- Triedenie ľavej polovice poľa.
- Triedenie pravej polovice poľa.
- Zlúčenie oboch polovíc pomocou funkcie Merge.
Slovný opis
Našou úlohou je vzostupne (min -> max) utriediť vstupné pole. Určíme si stred poľa (pri párnom počte prvkov je to ten menší z prostredných indexov). Následne vykonávame sériu rekurzívnych delení pre ľavú a pravú časť poľa (začiatok ... stred ; stred + 1 ... koniec) až do momentu, keď nám ostanú len jednoprvkové podpolia (tie sú už utriedené). Následne v každom volaní obe tieto podpolia zlúčime pomocou algoritmu Merge do väčších podpolí (max: 2, 4, 8, ...), až nakoniec dostaneme jedno výsledné utriedené pole.
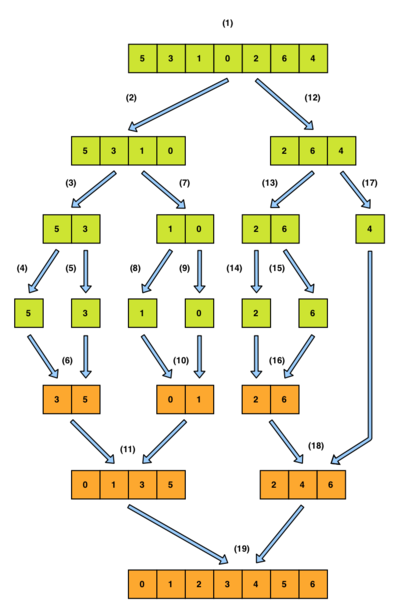
Pseudokód
Nech má funkcia MergeSort nasledovný prototyp: MergeSort(pole[], lavy, pravy)
- 1. Je
lavy >= pravy? Ak áno, skonči volanie, inak pokračuj krokom 2. - 2. Nech:
stred = lavy + (pravy - lavy) / 2, pričom znak / vyjadruje celočíselné delenie. - 3. Rekurzívne zavolaj funkciu
MergeSort(pole[], lavy , stred) - 3. Rekurzívne zavolaj funkciu
MergeSort(pole[], stred + 1 , pravy) - 4. Zavolaj funkciu
Merge(pole[], lavy, stred, pravy) - 5. Skonči volanie.
Základné časti algoritmu
- Určenie maximálnej veľkosti podpoľa na zlučovanie.
- Prechádzanie jednotlivých podpolí v poli.
- Zlučovanie jednotlivých podpolí pomocou funkcie Merge.
Slovný opis
Vstupné pole, ktoré má N prvkov, môžeme chápať, ako N rôznych jednoprvkových (utriedených) podpolí, ktoré máme zlúčiť do jedného výsledného N - prvkového utriedeného poľa. Keďže by bolo veľmi nepraktické zlučovať N podpolí naraz, zvolíme nasledovnú stratégiu: Budeme prechádzať dané pole od začiatku po koniec a v prvej iterácii zlúčime každé dva prvky, čím dostaneme [math]\frac{N}{2}[/math] dvojprvkových utriedených podpolí. Potom v druhej iterácii zlúčime každé 4 prvky do jedného podpoľa, v treťom cykle každých 8, ..., až do momentu, keď dostaneme jedno výsledné utriedené pole. Aby sme mohli túto stratégiu implementovať, potrebujeme dva cykly: vonkajší, ktorý nastaví maximálnu veľkosť podpoľa, ktoré ideme zlučovať (1,2,4,8 ... dlzka - 1) a vnútorný, ktorý prechádza jednotlivé podpolia. Následne už iba voláme funkciu Merge, ktorá dané podpolia zlučuje.
Poznámka, ak máme pole, ktoré má nepárny počet prvkov, tak ten posledný prvok nezlúčime hneď v prvej iterácii, ale až v tých ďalších. Takisto, ak N nie je mocnina čísla 2, tak musíme samozrejme ošetriť situáciu, kedy by sme sa dostali mimo rozsah poľa (Ak máme napríklad pole, čo má 7 prvkov, tak po prvej iterácii budú prvky utiredené podľa vzoru 2 + 2 + 2 + 1, po druhej 4 + 3, a po tretej 7 + 0)
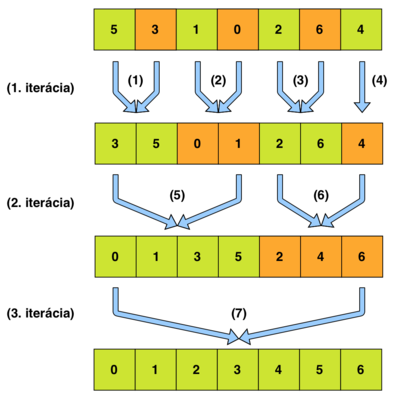
Pseudokód
Nech nech má funkcia MergeSort nasledovný prototyp: MergeSort(pole[], lavy, pravy)
- 1. Je
lavy >= pravy? Ak áno, skonči, inak pokračuj krokom 2. - 2. Nech:
dlzka_podpola = 1 - 3. Nech:
zaciatok = lavy - 4. Je
dlzka_podpola <= pravy? Ak áno pokračuj krokom 4.1, inak skonči.- 4.1. Je
zaciatok < pravyAk áno pokračuj krokom 4.1.1, inak skoč na krok 4.2.- 4.1.1. Je
zaciatok + 2 * dlzka_zoznamu - 1 <= pravy?- Ak áno:
- 4.1.1.1. Nech:
koniec = zaciatok + 2 * dlzka_podpola - 1
- 4.1.1.1. Nech:
- Ak nie:
- 4.1.1.1. Nech:
koniec = pravy
- 4.1.1.1. Nech:
- Ak áno:
- 4.1.2. Je
zaciatok + dlzka_podpola - 1 <= pravy?- Ak áno:
- 4.1.2.1. Nech
stred = zaciatok + dlzka_podpola - 1
- 4.1.2.1. Nech
- Ak nie:
- 4.1.2.1. Nech
stred = pravy
- 4.1.2.1. Nech
- Ak áno:
- 4.1.3.
Merge(pole[], zaciatok, stred, koniec) - 4.1.4.
zaciatok += 2 * dlzka_podpola - 4.1.5. Skoč na krok 4.1.
- 4.1.1. Je
- 4.2.
dlzka_podpole *= 2 - 4.3. Skoč na krok 4.
- 4.1. Je
Implementácia algoritmov Merge a MergeSort v rôznych programovacích jazykoch
#include <stdio.h>
#include <stdlib.h>
void Merge(int pole[], int lavy, int stred, int pravy);
void MergeSort(int pole[], int lavy, int pravy);
/* hlavný program */
int main()
{
int pole[] = {12, 11, 13, 5, 6, 7};
int dlzka_pola = sizeof(pole) / sizeof(pole[0]);
printf("Pôvodné pole: \n");
for (int i = 0; i < dlzka_pola; ++i)
{
printf("%d ", pole[i]);
}
MergeSort(pole, 0, dlzka_pola - 1);
printf("\nUtriedené pole: \n");
for (int i = 0; i < dlzka_pola; ++i)
{
printf("%d ", pole[i]);
}
return 0;
}
void Merge(int pole[], int lavy, int stred, int pravy)
{
/* ak má pole menej ako 2 prvky, skonči */
if (lavy >= pravy)
{
return;
}
/* vyrátaj dĺžky oboch polovíc poľa */
int L_dlzka = stred - lavy + 1;
int P_dlzka = pravy - stred;
/* alokuj dočasné polia, kam uložíš prvky z oboch polovíc poľa */
int *L = (int*)malloc(L_dlzka * sizeof(int));
int *P = (int*)malloc(P_dlzka * sizeof(int));
/* indexy, ktorými iterujeme všetky polia: i pre L, j pre P, k pre pole */
int i, j, k;
/* skopíruj obsah oboch polovíc poľa do dočasných polí L a P */
for (i = 0; i < L_dlzka; ++i)
{
L[i] = pole[lavy + i];
}
for (j = 0; j < P_dlzka; ++j)
{
P[j] = pole[stred + 1 + j];
}
/* nastav indexy na začiatok daných polí */
i = 0; j = 0; k = lavy;
/* zlučuj dočasné polia L a P do finálneho poľa pole */
while(i < L_dlzka && j < P_dlzka)
{
if(L[i] <= P[j])
{
pole[k++] = L[i++];
}
else
{
pole[k++] = P[j++];
}
}
/* ak ostali nejaké prvky v dočasnom poli L, skopíruj ich do finálneho poľa */
while(i < L_dlzka)
{
pole[k++] = L[i++];
}
/* ak ostali nejaké prvky v dočasnom poli P, skopíruj ich do finálneho poľa */
while(j < P_dlzka)
{
pole[k++] = P[j++];
}
/* uvoľni použitú pamäť */
free(L);
free(P);
}
void MergeSort(int pole[], int lavy, int pravy)
{
/* ak má pole menej ako 2 prvky, skonči volanie */
if(lavy >= pravy)
{
return;
}
/* urči si prostredný index */
int stred = lavy + (pravy - lavy) / 2;
/* utrieď ľavú polovicu poľa */
MergeSort(pole, lavy, stred);
/* utrieď pravú polovicu poľa */
MergeSort(pole, stred+1, pravy);
/* zlúč obe polovice dokopy */
Merge(pole, lavy, stred, pravy);
}
#include <stdio.h>
#include <stdlib.h>
void Merge(int pole[], int lavy, int stred, int pravy);
void MergeSortIt(int *pole, int lavy, int pravy);
/* hlavný program */
int main()
{
int pole[] = {12, 11, 13, 5, 6, 7, 19};
int dlzka_pola = sizeof(pole) / sizeof(pole[0]);
printf("Pôvodné pole %d: \n", dlzka_pola);
for (int i = 0; i < dlzka_pola; ++i)
{
printf("%d ", pole[i]);
}
MergeSortIt(pole, 0, dlzka_pola - 1);
printf("\nUtriedené pole: \n");
for (int i = 0; i < dlzka_pola; ++i)
{
printf("%d ", pole[i]);
}
return 0;
}
void Merge(int pole[], int lavy, int stred, int pravy)
{
/* ak má pole menej ako 2 prvky, skonči */
if (lavy >= pravy)
{
return;
}
/* vyrátaj dĺžky oboch polovíc poľa */
int L_dlzka = stred - lavy + 1;
int P_dlzka = pravy - stred;
/* alokuj dočasné polia, kam uložíš prvky z oboch polovíc poľa */
int *L = (int*)malloc(L_dlzka * sizeof(int));
int *P = (int*)malloc(P_dlzka * sizeof(int));
/* indexy, ktorými iterujeme všetky polia: i pre L, j pre P, k pre pole */
int i, j, k;
/* skopíruj obsah oboch polovíc poľa do dočasných polí L a P */
for (i = 0; i < L_dlzka; ++i)
{
L[i] = pole[lavy + i];
}
for (j = 0; j < P_dlzka; ++j)
{
P[j] = pole[stred + 1 + j];
}
/* nastav indexy na začiatok daných polí */
i = 0; j = 0; k = lavy;
/* zlučuj dočasné polia L a P do finálneho poľa pole */
while(i < L_dlzka && j < P_dlzka)
{
if(L[i] <= P[j])
{
pole[k++] = L[i++];
}
else
{
pole[k++] = P[j++];
}
}
/* ak ostali nejaké prvky v dočasnom poli L, skopíruj ich do finálneho poľa */
while(i < L_dlzka)
{
pole[k++] = L[i++];
}
/* ak ostali nejaké prvky v dočasnom poli P, skopíruj ich do finálneho poľa */
while(j < P_dlzka)
{
pole[k++] = P[j++];
}
/* uvoľni použitú pamäť */
free(L);
free(P);
}
void MergeSortIt(int *pole, int lavy, int pravy)
{
/* ak má pole menej ako 2 prvky, skonči volanie */
if(lavy >= pravy)
{
return;
}
int stred, koniec;
for (int dlzka_podpola = 1; dlzka_podpola <= pravy; dlzka_podpola *= 2)
{
for (int zaciatok = lavy; zaciatok < pravy; zaciatok += 2 * dlzka_podpola)
{
koniec = (zaciatok + 2 * dlzka_podpola - 1 <= pravy) ? zaciatok + 2 * dlzka_podpola - 1 : pravy;
stred = (zaciatok + dlzka_podpola - 1 <= pravy) ? zaciatok + dlzka_podpola - 1 : pravy;
Merge(pole, zaciatok, stred, koniec);
}
}
}
#include <iostream>
using std::cout;
using std::endl;
void Merge(int pole[], int lavy, int stred, int pravy);
void MergeSort(int pole[], int lavy, int pravy);
/* hlavný program */
int main()
{
int pole[] = {12, 11, 13, 5, 6, 7};
int dlzka_pola = sizeof(pole) / sizeof(pole[0]);
printf("Pôvodné pole: \n");
for (auto i: pole)
{
cout<<i<<" ";
}
MergeSort(pole, 0, dlzka_pola - 1);
cout<<endl<<"Utriedené pole:"<<endl;
for (auto i: pole)
{
cout<<i<<" ";
}
return 0;
}
void Merge(int pole[], int lavy, int stred, int pravy)
{
/* ak má pole menej ako 2 prvky, skonči */
if (lavy >= pravy)
{
return;
}
/* vyrátaj dĺžky oboch polovíc poľa */
int L_dlzka = stred - lavy + 1;
int P_dlzka = pravy - stred;
/* alokuj dočasné polia, kam uložíš prvky z oboch polovíc poľa */
int *L = new int[L_dlzka];
int *P = new int[P_dlzka];
/* indexy, ktorými iterujeme všetky polia: i pre L, j pre P, k pre pole */
int i, j, k;
/* skopíruj obsah oboch polovíc poľa do dočasných polí L a P */
for (i = 0; i < L_dlzka; ++i)
{
L[i] = pole[lavy + i];
}
for (j = 0; j < P_dlzka; ++j)
{
P[j] = pole[stred + 1 + j];
}
/* nastav indexy na začiatok daných polí */
i = 0; j = 0; k = lavy;
/* zlučuj dočasné polia L a P do finálneho poľa pole */
while(i < L_dlzka && j < P_dlzka)
{
if(L[i] <= P[j])
{
pole[k++] = L[i++];
}
else
{
pole[k++] = P[j++];
}
}
/* ak ostali nejaké prvky v dočasnom poli L, skopíruj ich do finálneho poľa */
while(i < L_dlzka)
{
pole[k++] = L[i++];
}
/* ak ostali nejaké prvky v dočasnom poli P, skopíruj ich do finálneho poľa */
while(j < P_dlzka)
{
pole[k++] = P[j++];
}
/* uvoľni použitú pamäť */
delete []L;
delete []P;
}
void MergeSort(int pole[], int lavy, int pravy)
{
/* ak má pole menej ako 2 prvky, skonči volanie */
if(lavy >= pravy)
{
return;
}
/* urči si prostredný index */
int stred = lavy + (pravy - lavy) / 2;
/* utrieď ľavú polovicu poľa */
MergeSort(pole, lavy, stred);
/* utrieď pravú polovicu poľa */
MergeSort(pole, stred+1, pravy);
/* zlúč obe polovice dokopy */
Merge(pole, lavy, stred, pravy);
}
#include <iostream>
using std::cout;
using std::endl;
void Merge(int pole[], int lavy, int stred, int pravy);
void MergeSortIt(int *pole, int lavy, int pravy);
/* hlavný program */
int main()
{
int pole[] = {12, 11, 13, 5, 6, 7};
int dlzka_pola = sizeof(pole) / sizeof(pole[0]);
printf("Pôvodné pole: \n");
for (auto i: pole)
{
cout<<i<<" ";
}
MergeSortIt(pole, 0, dlzka_pola - 1);
cout<<endl<<"Utriedené pole:"<<endl;
for (auto i: pole)
{
cout<<i<<" ";
}
return 0;
}
void Merge(int pole[], int lavy, int stred, int pravy)
{
/* ak má pole menej ako 2 prvky, skonči */
if (lavy >= pravy)
{
return;
}
/* vyrátaj dĺžky oboch polovíc poľa */
int L_dlzka = stred - lavy + 1;
int P_dlzka = pravy - stred;
/* alokuj dočasné polia, kam uložíš prvky z oboch polovíc poľa */
int *L = new int[L_dlzka];
int *P = new int[P_dlzka];
/* indexy, ktorými iterujeme všetky polia: i pre L, j pre P, k pre pole */
int i, j, k;
/* skopíruj obsah oboch polovíc poľa do dočasných polí L a P */
for (i = 0; i < L_dlzka; ++i)
{
L[i] = pole[lavy + i];
}
for (j = 0; j < P_dlzka; ++j)
{
P[j] = pole[stred + 1 + j];
}
/* nastav indexy na začiatok daných polí */
i = 0; j = 0; k = lavy;
/* zlučuj dočasné polia L a P do finálneho poľa pole */
while(i < L_dlzka && j < P_dlzka)
{
if(L[i] <= P[j])
{
pole[k++] = L[i++];
}
else
{
pole[k++] = P[j++];
}
}
/* ak ostali nejaké prvky v dočasnom poli L, skopíruj ich do finálneho poľa */
while(i < L_dlzka)
{
pole[k++] = L[i++];
}
/* ak ostali nejaké prvky v dočasnom poli P, skopíruj ich do finálneho poľa */
while(j < P_dlzka)
{
pole[k++] = P[j++];
}
/* uvoľni použitú pamäť */
delete []L;
delete []P;
}
void MergeSortIt(int *pole, int lavy, int pravy)
{
/* ak má pole menej ako 2 prvky, skonči volanie */
if(lavy >= pravy)
{
return;
}
int stred, koniec;
for (int dlzka_podpola = 1; dlzka_podpola <= pravy; dlzka_podpola *= 2)
{
for (int zaciatok = lavy; zaciatok < pravy; zaciatok += 2 * dlzka_podpola)
{
koniec = (zaciatok + 2 * dlzka_podpola - 1 <= pravy) ? zaciatok + 2 * dlzka_podpola - 1 : pravy;
stred = (zaciatok + dlzka_podpola - 1 <= pravy) ? zaciatok + dlzka_podpola - 1 : pravy;
Merge(pole, zaciatok, stred, koniec);
}
}
}
class MergeSort
{
/* Funkcia zlúči 2 podpolia, ktoré sme vytvorili z pôvodného poľa.
* Každé podpole má polovičnú dĺžku pôvodného poľa.
* podpole1 [ľavý ... stred]
* podpole2 [stred + 1 ... pravý]
*/
void merge(int[] pole, int lavy, int stred, int pravy)
{
// Výpočet dĺžky 2 podpolí
int n1 = stred - lavy + 1;
int n2 = pravy - stred;
// Vytvorenie pomocných polí
int[] L = new int[n1];
int[] P = new int[n2];
// Načítanie dát do pomocných polí
for (int i = 0; i < n1; i++)
L[i] = pole[lavy + i];
for (int j = 0; j < n2; j++)
P[j] = pole[stred + 1 + j];
// Počiatočné indexy prvého a druhého podpoľa
int i = 0, j = 0;
// Počiatočný index zlúčeného podpoľa
int k = lavy;
// Zlúčenie dvoch podpolí
while (i < n1 && j < n2)
{
if (L[i] <= P[j])
{
pole[k] = L[i];
i++;
}
else
{
pole[k] = P[j];
j++;
}
k++;
}
/* V prípade, že sa v jednom zo podpolí nachádzajú ešte nejaké prvky, ktoré neboli zlúčené do poľa,
* tak sa do poľa jednoducho skopírujú
*/
while (i < n1)
{
pole[k] = L[i];
i++;
k++;
}
while (j < n2)
{
pole[k] = P[j];
k++;
j++;
}
}
/* Funkcia, ktorá zoradí pole použitím funkcie merge() */
void sort (int[] pole, int lavy, int pravy)
{
if (lavy < pravy)
{
// Musíme nájsť stred poľa
int stred = lavy + (pravy - lavy) / 2;
// Zoradíme prvú a druhú polovicu poľa samostatne
sort(pole, lavy, stred);
sort(pole, stred + 1, pravy);
// Zlúčime zoradené polovice do jedného poľa
merge(pole, lavy, stred, pravy);
}
}
}
public class Main
{
/* Funkcia na výpis poľa dĺžky n */
static void vypis_pole(int[] pole)
{
for (int j : pole)
{
System.out.print(j + " ");
}
System.out.println();
}
/* Hlavný program */
public static void main(String[] args)
{
int[] pole = {12, 11, 13, 5, 6, 7};
System.out.println("Zadané pole:");
vypis_pole(pole);
MergeSort ms = new MergeSort();
ms.sort(pole, 0, pole.length - 1);
System.out.println("\nZoradené pole:");
vypis_pole(pole);
}
}
class MergeSort_iteracia
{
/* Zlúči 2 podpolia, ktoré sa vytvorili z pôvodného poľa.
* Každé podpole má polovičnú dĺžku pôvodného poľa.
* podpole1 [ľavý..stred]
* podpole2 [stred+1..pravý]
*/
void merge(int[] pole, int lavy, int stred, int pravy)
{
// Výpočet dĺžky 2 podpolí
int n1 = stred - lavy + 1;
int n2 = pravy - stred;
// Vytvorenie pomocných polí
int[] L = new int[n1];
int[] P = new int[n2];
// Načítanie dát do pomocných polí
for (int i = 0; i < n1; i++)
L[i] = pole[lavy + i];
for (int j = 0; j < n2; j++)
P[j] = pole[stred + 1 + j];
// Počiatočné indexy prvého a druhého podpoľa
int i = 0, j = 0;
// Počiatočný index zlúčeného podpoľa
int k = lavy;
// Zlúčenie dvoch podpolí
while (i < n1 && j < n2)
{
if (L[i] <= P[j])
{
pole[k] = L[i];
i++;
}
else
{
pole[k] = P[j];
j++;
}
k++;
}
/* V prípade, že v jednom z podpolí sa nachádzajú prvky, ktoré neboli zlúčené do poľa,
* tak sa do poľa jednoducho skopírujú
*/
while (i < n1)
{
pole[k] = L[i];
i++;
k++;
}
while (j < n2)
{
pole[k] = P[j];
k++;
j++;
}
}
/* Funkcia, ktorá zoradí pole použitím funkcie merge() */
void sort (int[] pole, int n)
{
/* Dĺžka podpolí, ktoré majú byť zlúčené, hodnoty premennej sa pohybujú v intervale <1;n-1> */
int aktual_dlzka;
/* Začiatočný index ľavého podpoľa, ktoré má byť zlúčené */
int zaciatok_vlavo;
/* Vzostupné usporiadanie prvkov. Najskôr sa zlúčia podpolia veľkosti 1 do podpolí veľkosti 2,
* potom podpolia veľkosti 2 do podpolí veľkosti 4 a tak ďalej
*/
for (aktual_dlzka = 1; aktual_dlzka <= n - 1; aktual_dlzka *= 2)
{
/* Určenie začiatočného prvku rôznych podpolí aktuálnej dĺžky podpoľa */
for (zaciatok_vlavo = 0; zaciatok_vlavo < n - 1; zaciatok_vlavo += 2 * aktual_dlzka)
{
/* Nájdenie konečného prvku ľavého podpoľa, stred+1 je začiatočný prvok pravého podpoľa */
int stred = Math.min(zaciatok_vlavo + aktual_dlzka - 1, n - 1);
int koniec_vpravo = Math.min(zaciatok_vlavo + 2 * aktual_dlzka - 1, n - 1);
/* Zlúči podpolia L[zaciatok_vlavo .. stred] & P[stred+1 .. koniec_vpravo] */
merge(pole, zaciatok_vlavo, stred, koniec_vpravo);
}
}
}
}
public class Main {
/* Funkcia na výpis poľa dĺžky n */
static void vypis_pole(int[] pole)
{
int n = pole.length;
for (int j : pole)
{
System.out.print(j + " ");
}
System.out.println();
}
/* Hlavný program */
public static void main(String[] args) {
/* Inicializácia poľa */
int[] pole = {12, 11, 13, 5, 6, 7};
System.out.println("Zadané pole:");
vypis_pole(pole);
MergeSort_iteracia ms_it = new MergeSort_iteracia();
ms_it.sort(pole, pole.length);
System.out.println("Zoradené pole:");
vypis_pole(pole);
}
}
def MergeSort(pole):
if len(pole) > 1:
# Nájdenie stredu poľa
# zápis len(pole)//2 znamená, že dĺžka poľa sa vydelí 2 a výsledok je celé číslo
stred = len(pole) // 2
# Rozdelenie poľa na dve časti
L = pole[:stred]
P = pole[stred:]
# Zoradenie najskôr prvej časti poľa, potom druhej
MergeSort(L)
MergeSort(P)
i = j = k = 0
# Zlúčenie a zoradenie údajov z pomocných polí do jedného poľa
while i < len(L) and j < len(P):
if L[i] < P[j]:
pole[k] = L[i]
i += 1
else:
pole[k] = P[j]
j += 1
k += 1
# Kontrola či všetky prvky boli zlúčené dokopy,
# ak nie, tak sa do zlúčeného poľa jednoducho skopírujú
while i < len(L):
pole[k] = L[i]
i += 1
k += 1
while j < len(P):
pole[k] = P[j]
j += 1
k += 1
# Hlavný program
if __name__ == '__main__':
pole = [12, 11, 13, 5, 6, 7]
print("Zadané pole:", end="\n")
print(pole, end="\n")
MergeSort(pole)
print("Zoradené pole:", end="\n")
print(pole, end="\n")
def MergeSort_iteracia(pole):
# Dĺžka podpolí, ktoré majú byť zlúčené, hodnoty premennej sa pohybujú v intervale <1;n-1>
aktual_dlzka = 1
# Vonkajší cyklus, ktorý určuje podpolia aktuálnej dĺžky
while aktual_dlzka < len(pole) - 1:
lavy = 0
# Vnútorný cyklus, ktorý slúži na zlúčenie a zoradenie podpolí do jedného podpoľa
while lavy < len(pole) - 1:
# Index stredného prvku sa určí, keď k indexu ľavého prvku podpoľa pripočítame aktuálnu
# dĺžku podpolí a odčítame 1
stred = min((lavy + aktual_dlzka - 1), len(pole) - 1)
# Ak platí podmienka 2 * aktuálna dĺžka < dĺžka poľa - 1, tak pravý index = aktuálnej dĺžke subpolí,
# inak pravý index = dĺžka poľa - 1
pravy = ((2 * aktual_dlzka + lavy - 1, len(pole) - 1)[2 * aktual_dlzka + lavy - 1 > len(pole) - 1])
# Volanie funkcie merge
merge(pole, lavy, stred, pravy)
lavy = lavy + 2 * aktual_dlzka
# Aktuálna dĺžka sa sa zmení na dvojnásobok jej predošlej hodnoty
aktual_dlzka = 2 * aktual_dlzka
def merge(pole, lavy, stred, pravy):
n1 = stred - lavy + 1
n2 = pravy - stred
# Inicializácia pomocných polí
L = [0] * n1
P = [0] * n2
# Načítanie dát do pomocných polí
for i in range(0, n1):
L[i] = pole[lavy + i]
for i in range(0, n2):
P[i] = pole[stred + i + 1]
i, j, k = 0, 0, lavy
# Zlúčenie a zoradenie údajov z pomocných polí do jedného poľa
while i < n1 and j < n2:
if L[i] > P[j]:
pole[k] = P[j]
j += 1
else:
pole[k] = L[i]
i += 1
k += 1
# Kontrola či všetky prvky boli zlúčené dokopy,
# ak nie, tak sa do zlúčeného pola jednoducho skopírujú
while i < n1:
pole[k] = L[i]
i += 1
k += 1
while j < n2:
pole[k] = P[j]
j += 1
k += 1
# Hlavný program
if __name__ == '__main__':
pole = [12, 11, 13, 5, 6, 7]
print("Zadané pole:", end="\n")
print(pole, end="\n")
MergeSort_iteracia(pole)
print("Zoradené pole:", end="\n")
print(pole, end="\n")
Odkazy
- https://www.geeksforgeeks.org/merge-sort/
- https://www.geeksforgeeks.org/iterative-merge-sort/
- https://medium.com/@paulsoham/merge-sort-63d75df76388
- https://www.khanacademy.org/computing/computer-science/algorithms/merge-sort/a/overview-of-merge-sort
- https://www.tutorialspoint.com/data_structures_algorithms/merge_sort_algorithm.htm
- https://www.youtube.com/watch?v=6pV2IF0fgKY
- https://www.youtube.com/watch?v=mB5HXBb_HY8
- https://www.youtube.com/watch?v=ak-pz7tS5DE