Triedenie zlučovaním: Rozdiel medzi revíziami
| Riadok 261: | Riadok 261: | ||
public class Main { | public class Main { | ||
/* Funkcia na výpis pola dĺžky n */ | /* Funkcia na výpis pola dĺžky n */ | ||
| − | static void | + | static void vypis_pole(int[] pole) { |
int n = pole.length; | int n = pole.length; | ||
| Riadok 275: | Riadok 275: | ||
System.out.println("Zadané pole:"); | System.out.println("Zadané pole:"); | ||
| − | + | vypis_pole(pole); | |
MergeSort ms = new MergeSort(); | MergeSort ms = new MergeSort(); | ||
| Riadok 281: | Riadok 281: | ||
System.out.println("\nZoradené pole:"); | System.out.println("\nZoradené pole:"); | ||
| − | + | vypis_pole(pole); | |
} | } | ||
} | } | ||
Verzia zo dňa a času 15:29, 23. marec 2021
TREBA SKONTROLOVAŤ PSEUDOKÓDY!!!
Zlučovacia funkcia Merge:
Funkcia Merge je zlučovacia funkcia, ktorá tvorí základ triediaceho algoritmu Merge sort.
Princíp zlučovania:
Vo všeobecnosti princíp zlučovania tkvie v tom, že zoberieme dva (alebo viac) menšie utriedné zoznamy, ktoré skombinujeme do jedného väčšieho utriedeného zoznamu. Zoznam môže byť reprezentovaný ako dátová štruktúra pole alebo aj ako lineárny zoznam. V tejto časti sa zameriame na algoritmus pre dátovú štruktúru pole.
Slovný opis algoritmu:
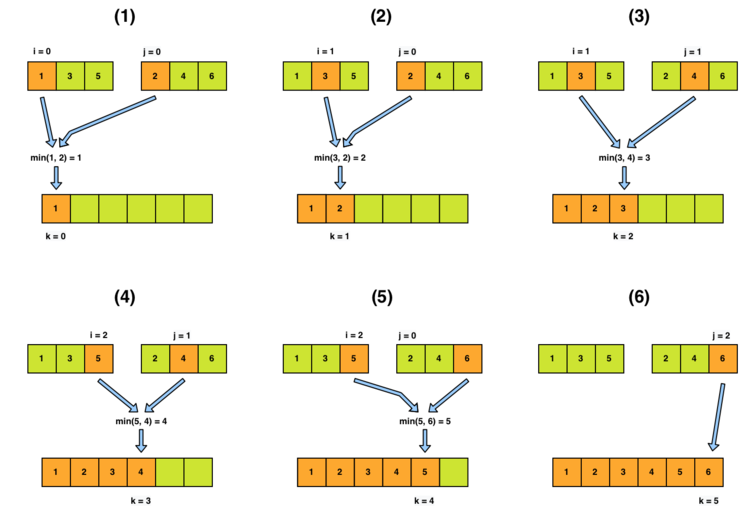
Pri funkcii Merge využívame princíp zlučovania tak, že máme pole, ktoré sa skladá z dvoch už utriedených polovíc. Následne si vytvoríme dve pomocné polia, do ktorých skopíruje obsahy oboch polovíc. Potom súčasne prechádzame obe pomocné polia a vždy z uvažovanej dvojice prvkov vyberáme ten menší z nich (keď triedime od najväčšieho po najmenší) a vložíme ho na začiatok pôvodného poľa. Index zvýšime iba pri tom poli z ktorého sme daný prvok vybrali. Ak nastane situácia, že z jedného pomocného poľa vyberieme všetky prvky skôr, ako z druhého pomocného poľa, potom zbytok druhého pomocného poľa už iba kopírujeme na koniec pôvodného poľa.
Vzorový príklad:
Máme pole prvkov p = [1, 3, 5, 2, 4, 6], ktoré je už čiastočne utriedené. Použijeme algoritmus Merge, ktorý si vyptvorí pomocné polia L = [1, 3, 5] a P = [2, 4, 6]. Všetky polia indexujeme od 0, pričom pre pole p používame index k, pre L index i a P index j.
Pseudokód
Nech funkcia Merge má parametre, pole[], lavy, stred a pravy.
- 1. Nech:
i = 0, j = 0, k = lavy - 2. Nech:
dlzka_L = stred - lavy + 1, dlzka_P = pravy - stred - 3. Nech:
L = pole[lavy ... stred], P = pole[stred + 1 ... pravy] - 4. Je
i < dlzka_La zároveňj < dlzka_P? Ak áno, pokračuj krokom 3.1., inak skok na krok 5.- 4.1. Je
L[i] <= P[j]? Ak áno,pole[k++] = L[i++], inakpole[k++] = P[j++]. - 4.2. Skok na krok 4.
- 4.1. Je
- 5. Je
i < dlzka_L? Ak áno, pokračuj krokom 4.1., inak skok na krok 6.- 5.1.
pole[k++] = L[i++] - 5.2. Skok na krok 5.
- 5.1.
- 6. Je
j < dlzka_P? Ak áno, pokračuj krokom 5.1., inak skonči program.- 6.1.
pole[k++] = P[j++] - 6.2. Skok na krok 6.
- 6.1.
Merge sort
Merge Sort je triediaci algoritmus, ktorý je založený na princípe "rozdeľ a panuj", čo znamená, že pole najskôr rozdelí na dve polovice, tie zoradí a potom ich zlúči naspäť dokopy. Keďže najhoršia doba výpočtu je [math]O(n.log(n))[/math], tak sa radí medzi najpoužívanejšie a najviac rešpektované triediacie algoritmy.
Princíp algoritmu
Algoritmus Merge vykonáva 4 základné úlohy:
- Delenie poľa na dve polovice.
- Triedenie ľavej polovice poľa.
- Triedenie pravej polovice poľa.
- Zlúčenie oboch polovíc pomocou funkcie Merge.
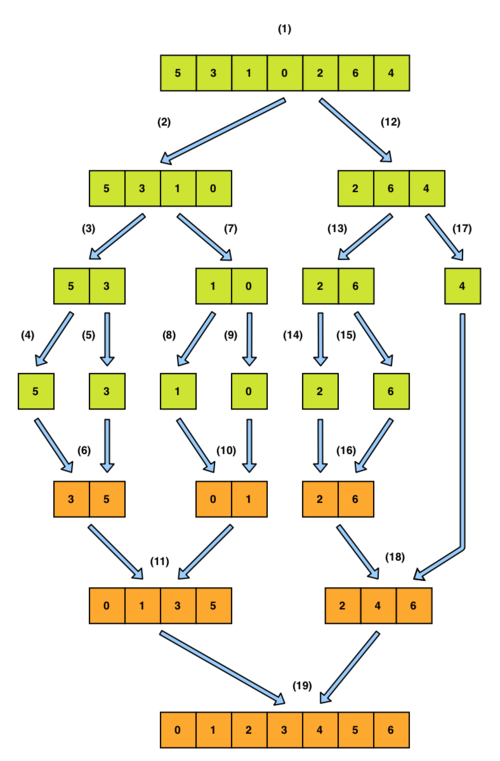
Vizualizácia algoritmu
Pseudokód
Nech nech má funkcia MergeSort nasledovný prototyp: MergeSort(pole[], lavy, pravy)
- 1. Je
lavy >= pravy? Ak áno, skonči volanie, inak pokračuj krokom 2. - 2. Nech:
stred = lavy + (pravy - lavy) / 2, pričom stred musí byť typu int (celé číslo) - 3. Rekurzívne zavolaj funkciu
MergeSort(pole[], lavy , stred) - 3. Rekurzívne zavolaj funkciu
MergeSort(pole[], stred + 1 , pravy) - 4 Zavolaj funkciu
Merge(pole[], lavy, stred, pravy) - 5 Skonči volanie.
Implementácia v jazyku C
1 void Merge(int pole[], int lavy, int stred, int pravy);
2 void MergeSort(int pole[], int lavy, int pravy);
3
4 /* hlavný program */
5
6 int main()
7 {
8 int pole[] = {12, 11, 13, 5, 6, 7};
9 int dlzka_pola = sizeof(pole) / sizeof(pole[0]);
10
11 printf("Pôvodné pole: \n");
12
13 for (int i = 0; i < dlzka_pola; ++i)
14 {
15 printf("%d ", pole[i]);
16 }
17
18 MergeSort(pole, 0, dlzka_pola - 1);
19
20 printf("\nUtriedené pole: \n");
21
22 for (int i = 0; i < dlzka_pola; ++i)
23 {
24 printf("%d ", pole[i]);
25 }
26
27 return 0;
28 }
29
30 void Merge(int pole[], int lavy, int stred, int pravy)
31 {
32 /* ak má pole menej ako 2 prvky, skonči */
33
34 if (lavy >= pravy)
35 {
36 return;
37 }
38
39 /* vyrátaj dĺžky oboch polovíc poľa */
40
41 int L_dlzka = stred - lavy + 1;
42 int P_dlzka = pravy - stred;
43
44 /* alokuj dočasné polia, kam uložíš prvky z oboch polovíc poľa */
45
46 int *L = (int*)malloc(L_dlzka * sizeof(int));
47 int *P = (int*)malloc(P_dlzka * sizeof(int));
48
49 /* indexy, ktorými iterujeme všetky polia: i pre L, j pre P, k pre pole */
50
51 int i, j, k;
52
53 /* skopíruj obsah oboch polovíc poľa do dočasných polí L a P */
54
55 for (i = 0; i < L_dlzka; ++i)
56 {
57 L[i] = pole[lavy + i];
58 }
59
60 for (j = 0; j < P_dlzka; ++j)
61 {
62 P[j] = pole[stred + 1 + j];
63 }
64
65 /* nastav indexy na začiatok daných polí */
66
67 i = 0; j = 0; k = lavy;
68
69 /* zlučuj dočasné polia L a P do finálneho poľa pole */
70
71 while(i < L_dlzka && j < P_dlzka)
72 {
73 if(L[i] <= P[j])
74 {
75 pole[k++] = L[i++];
76 }
77 else
78 {
79 pole[k++] = P[j++];
80 }
81 }
82
83 /* ak ostali nejaké prvky v dočasnom poli L, skopíruj ich do finálneho poľa */
84
85 while(i < L_dlzka)
86 {
87 pole[k++] = L[i++];
88 }
89
90 /* ak ostali nejaké prvky v dočasnom poli P, skopíruj ich do finálneho poľa */
91
92 while(j < P_dlzka)
93 {
94 pole[k++] = P[j++];
95 }
96
97 /* uvoľni použitú pamäť */
98
99 free(L);
100 free(P);
101 }
102
103 void MergeSort(int pole[], int lavy, int pravy)
104 {
105 /* ak má pole menej ako 2 prvky, skonči volanie */
106
107 if(lavy >= pravy)
108 {
109 return;
110 }
111 /* urči si prostredný index */
112
113 int stred = lavy + (pravy - lavy) / 2;
114
115 /* utrieď ľavú polovicu poľa */
116
117 MergeSort(pole, lavy, stred);
118
119 /* utrieď pravú polovicu poľa */
120
121 MergeSort(pole, stred+1, pravy);
122
123 /* zlúč obe polovice dokopy */
124
125 Merge(pole, lavy, stred, pravy);
126 }
Implementácia v jazyku Java
1 class MergeSort {
2 /* Zlúči 2 subpolia, ktoré sa vytvorili z pôvodného pola.
3 * Každé subpole má polovičnú dĺžku pôvodného pola.
4 * subpole1 [ľavý..stred]
5 * subpole2 [stred+1..pravý] */
6 void merge(int[] pole, int lavy, int stred, int pravy) {
7 // Výpočet dĺžky 2 subpolí
8 int n1 = stred - lavy + 1;
9 int n2 = pravy - stred;
10
11 // Vytvorenie pomocných polí
12 int[] L = new int[n1];
13 int[] P = new int[n2];
14
15 // Načítanie dát do pomocných polí
16 for (int i = 0; i < n1; i++)
17 L[i] = pole[lavy + i];
18
19 for (int j = 0; j < n2; j++)
20 P[j] = pole[stred + 1 + j];
21
22 // Počiatočné indexy prvého a druhého subpola
23 int i = 0, j = 0;
24 // Počiatočný index zlúčeného subpola
25 int k = lavy;
26
27 // Zlúčenie dvoch podpolí
28 while (i < n1 && j < n2) {
29 if (L[i] <= P[j]) {
30 pole[k] = L[i];
31 i++;
32 }
33 else {
34 pole[k] = P[j];
35 j++;
36 }
37 k++;
38 }
39
40 /* V prípade, že v jednom zo subpolí sa nachádzajú prvky, ktoré neboli zlúčené do pola,
41 * tak sa do pola jednoducho skopírujú */
42 while (i < n1) {
43 pole[k] = L[i];
44 i++;
45 k++;
46 }
47
48 while (j < n2) {
49 pole[k] = P[j];
50 k++;
51 j++;
52 }
53 }
54
55 /* Funkcia, ktorá zoradí pole použitím funkcie merge() */
56 void sort (int[] pole, int lavy, int pravy) {
57 if (lavy < pravy) {
58 //Musíme nájsť stred pola
59 int stred = lavy + (pravy - lavy) / 2;
60
61 // Zoradíme prvú a druhú polovicu pola samostatne
62 sort(pole, lavy, stred);
63 sort(pole, stred + 1, pravy);
64
65 // Zlúčime zoradené polovice do jedného pola
66 merge(pole, lavy, stred, pravy);
67 }
68 }
69 }
70
71 public class Main {
72 /* Funkcia na výpis pola dĺžky n */
73 static void vypis_pole(int[] pole) {
74 int n = pole.length;
75
76 for (int i = 0; i < n; i++) {
77 System.out.print(pole[i] + " ");
78 }
79 System.out.println();
80 }
81
82 /* Hlavný program */
83 public static void main(String[] args) {
84 int[] pole = {12, 11, 13, 5, 6, 7};
85
86 System.out.println("Zadané pole:");
87 vypis_pole(pole);
88
89 MergeSort ms = new MergeSort();
90 ms.sort(pole, 0, pole.length - 1);
91
92 System.out.println("\nZoradené pole:");
93 vypis_pole(pole);
94 }
95 }
Implementácia v jazyku Python3
1 def MergeSort(pole):
2 if len(pole) > 1:
3 # Nájdenie stredu pola
4 # zápis len(pole)//2 znamená, že dĺžka pola sa vydelí 2 a výsledok je celé číslo
5 stred = len(pole) // 2
6
7 # Rozdelenie pola na dve časti
8 L = pole[:stred]
9 P = pole[stred:]
10
11 # Zoradenie najskôr prvej časti pola, potom druhej
12 MergeSort(L)
13 MergeSort(P)
14
15 i = j = k = 0
16
17 # Načítanie dát do pomocných polí L[] a P[]
18 while i < len(L) and j < len(P):
19 if L[i] < P[j]:
20 pole[k] = L[i]
21 i += 1
22 else:
23 pole[k] = P[j]
24 j += 1
25 k += 1
26
27 # Kontrola či všetky prvky boli zlúčené dokopy,
28 # ak nie, tak sa do zlúčeného pola jednoducho skopírujú
29 while i < len(L):
30 pole[k] = L[i]
31 i += 1
32 k += 1
33
34 while j < len(P):
35 pole[k] = P[j]
36 j += 1
37 k += 1
38
39
40 # Kód na výpis pola
41 def vypis_pole(pole):
42 for i in range(len(pole)):
43 print(pole[i], end=" ")
44 print()
45
46
47 # Hlavný program
48 if __name__ == '__main__':
49 pole = [12, 11, 13, 5, 6, 7]
50 print("Zadané pole:", end="\n")
51 vypis_pole(pole)
52 MergeSort(pole)
53 print("Zoradené pole:", end="\n")
54 vypis_pole(pole)