Jazyk C (príklady) - Algoritmy: Rozdiel medzi revíziami
| (19 medziľahlých úprav od 2 ďalších používateľov nie je zobrazených) | |||
| Riadok 1: | Riadok 1: | ||
| − | + | [[Kategória:Študijné materiály]] | |
| − | + | [[Kategória:Informatika]] | |
| − | + | {{Priklady_ZI}} | |
| + | __TOC__ | ||
| + | ==Obsah== | ||
| + | V tejto kapitole budú ukázaná tvorba jednoduchých vývojových diagramov. Budú ukázané základné prvky algoritmizácie úloh, použitie rozhodovania, opakovania istého počtu operácií. K zvládnutiu tejto kapitoly sa predpokladá znalosť grafických značiek použitých pri tvorbe vývojových diagramov. | ||
| − | + | ===Grafické značky vývojových diagramov=== | |
| − | |||
| − | + | Medzi základné stavebné bloky vývojových diagramov (VD) patria bloky, ktoré reprezentujú | |
| − | |||
| − | |||
| + | *začiatok / koniec VD | ||
| + | *vykonávací blok | ||
| + | *rozhodovací blok | ||
| + | *spojka | ||
| + | *vstup / výstup dát | ||
| + | *orientované spojnice blokov | ||
| + | [http://www.kiwiki.info/index.php/Algoritmus[Vývojové stavebné bloky]] | ||
| − | |||
| − | |||
| − | == | + | ==Príklady== |
| − | |||
| − | + | ===Absolútna hodnota=== | |
| − | [[Súbor: | + | ;Zadanie: Vieme, že absolútna hodnota je definovaná ako vzdialenosť čísla od začiatku súradnicového systému (resp. od nuly). Nakreslite vývojový diagram, ktorý by znázorňoval výpočet absolútnej hodnoty. |
| + | |||
| + | ;Analýza problému: Pre absolútnu hodnotu reálnych čísel platí: | ||
| + | * abs(x) = x | ||
| + | * abs(-x) = x | ||
| + | Inak povedané, pre x>=0, je absolútna hodnota x rovná práve x, pre x<0 je absolútna hodnota x rovná -1*x. | ||
| + | Teda, stačí nám zistiť, či je x menšie ako nula. | ||
| + | |||
| + | [[Súbor:78 2 alg1.png|240px|none]] | ||
| + | |||
| + | |||
| + | ===Kvadratická rovnica=== | ||
| + | ;Zadanie: Navrhnite algoritmus výpočtu koreňov kvadratickej rovnice ax2+bx+c=0. Vstupom do algoritmu budú koeficienty a, b, c, a výstupom budú korene kvadratickej rovnice x1,2. | ||
| + | |||
| + | ;Analýza problému: Riešenie tejto rovnice je známe, úlohou je tento problém znázorniť v podobe vývojového diagramu. Vieme, že kvadratická rovnica má dva korene (x1 a x2). Tieto korene môžu byť rôzne, alebo riešením je jeden dvojnásobný koreň. Toto zistíme pomocou výpočtu diskriminantu kvadratickej rovnice. Diskriminant je definovaný ako D=b2-4ac | ||
| + | Rozoberme si jednotlivé prípady riešenia. | ||
| + | *D>0 : Rovnica má dva korene: x1=(-b+D1/2)/2a, x2=(-b-D1/2)/2a | ||
| + | *D=0 : Rovnica má jeden dvojnásobný koreň: x1,2=-b/2a | ||
| + | *D<0 : Rovnica má riešenie na množine komplexných čísel: | ||
| + | Vieme, že i2=-1. (i je komplexná jednotka). Potom výpočet druhej odmocniny diskriminantu je (D)1/2=(i2 * (-D))1/2=i*(-D) ½ (poznámka: D<0). Teda korene kvadratickej rovnice budú x1=(-b+iD1/2)/2a, x2=(-b-iD1/2)/2a | ||
| + | |||
| + | |||
| + | [[Súbor:80 2 alg2.png|480px|none]] | ||
| + | |||
| + | ===Maximum z 3 hodnôt=== | ||
| + | ;Zadanie: V predajni skrípt majú 3 skriptá, o ktoré máme záujem. Cena skrípt je a, b, c Sk. Navrhnite algoritmus, ktorý nájde najdrahšie skriptá; teda skriptá s maximálnou cenou. | ||
| + | |||
| + | ;Analýza problému: V prípade, ak máme zistiť maximálnu (alebo minimálnu) hodnotu z troch čísel, musíme každé číslo porovnať s každým iným číslom. Teda, spolu budeme robiť 3 porovnania (a<->b, a<->c, b<->c). Nemá zmysel porovnávať ab a ba, lebo toto sú totožné porovnania. Ak teda máme zistiť najväčšie číslo z a, b, c, môžeme postupovať napríklad nasledovne: Najskôr porovnáme : a>b. Ak toto platí, potom porovnáme a>c. V prípade ak aj toto platí, tak maximum je a. Keby platilo že: a>b a c>a, potom vieme, že maximum je c. Takto by sme mohli pokračovať ďalej. | ||
| + | |||
| + | |||
| + | [[Súbor:82 2 alg3.png|360px|none]] | ||
| + | |||
| + | |||
| + | ===Opakované načítanie=== | ||
| + | |||
| + | ;Zadanie: Na faktúre je údaj o počte položiek a samotné položky (položka obsahuje o.i. aj cenu v Sk). Ak viete koľko je na faktúre položiek, navrhnite algoritmus, ktorý vypočíta celkovú sumu položiek faktúry. Prvý vstupný údaj bude číslo pocet, ktoré nám hovorí o počte nasledujúcich položiek. Následne sa načíta pocet položiek ( – celých čísel symbolizujúcim cenu položky). Navrhnite algoritmus, ktorý vypočíta výslednú sumu ceny všetkých položiek. | ||
| + | |||
| + | ;Analýza problému: V tomto prípade nikdy popredu nevieme, koľko budeme načítavať položiek. Tento údaj sa dozvieme až v momente, keď načítame prvý údaj. Úlohou bude teda navrhnúť algoritmus, ktorý by načítal požadovaný počet položiek (počet položiek môže byť od 0 až po ľubovoľne veľké konečné číslo). Na riešenie tohto problému využijeme cyklus. Tento cyklus sa bude opakovať toľkokrát, koľko položiek máme načítať. Pri každom opakovaní cyklu načítame jednu položku (položku označme ako premennú a) a jej hodnotu pripočítame k výslednej sume. Ďalším algoritmickým problémom je zabezpečiť, aby sa tento cyklus vykonával presne pocet krát. Tu využijeme prvý vstupný údaj pocet. Pri každej iterácii (opakovaní) cyklu sa hodnota premennej pocet zníži o 1. Cyklus budeme opakovať dovtedy, pokiaľ bude premenná pocet rôzna od nuly. Na výpočet súčtu všetkých položiek využijeme premennú suma, ktorú na začiatku vynulujeme (priradíme jej hodnotu 0). | ||
| + | |||
| + | |||
| + | [[Súbor:84 2 alg4.png|360px|none]] | ||
| + | |||
| + | |||
| + | ===Násobenie=== | ||
| + | |||
| + | ;Zadanie: V počítačoch (na hardvérovej úrovni) sa operácia násobenia vykoná pomocou opakovaného sčítavania dvoch hodnôt. Vytvorte algoritmus, ktorý by násobil dve celé čísla pomocou opakovaného sčítavania. | ||
| + | |||
| + | ;Analýza problému: Na riešenie problému nemôžeme použiť operáciu násobenia (*), musíme použiť operáciu sčítavania (+). Zoberme si príklad: x=5*3. Tu budeme 3 krát pripočítame hodnotu 5 do premennej x, ktorú musíme najskôr vynulovať. Teda x=5+5+5=15. Vo všeobecnosti máme x=a*b=a+a+...+a : sčítavanie robíme b krát. Z uvedeného vyplýva, že nemôžeme pevne napísať, koľkokrát sa a pripočíta do premennej x. Tu bude vhodné využiť nejaký cyklus. V každom cykle sa do premennej x pripočíta hodnota a. Počet opakovaní cyklu je b. V každej iterácii cyklu hodnotu premennej b znížime o 1. Cyklus ukončíme, ak sa b=0. | ||
| + | |||
| + | |||
| + | [[Súbor:86 2 alg5.png|300px|none]] | ||
| + | |||
| + | ===Prvočíslo=== | ||
| + | ;Zadanie: Navrhnite algoritmus, ktorý zistí, či zadané číslo a je prvočíslo. | ||
| + | |||
| + | ;Analýza problému: Prvočíslo je číslo, ktoré je delitelné iba číslom 1 a sebou samým. Pri testovaní čísla a na prvočíselnosť postupne celočíselne deliť číslo a číslami del=2, 3, ...n. Ak pri všetkých deleniach bude nejaký zvyšok (a sa nedá deliť číslom del), povieme že číslo a je prvočíslo. Ak v priebehu delenia zistíme, že a je delitené číslom del bezo zvyšku, algoritmus ukončíme, a povieme že a nie je prvočíslo. Ďalší problém je určiť, dokedy má zmysel zväčšovať deliteľ del. V predchádzajúcom texte sme del zvyšovali po hodnotu n. Úlohou je odhadnúť vhodné n. Pokúsme sa postupovať nasledovne: ako prvý deliteľ je del=2. Teda delíme a číslom del=2. Výsledok po tomto delení označme podiel. Ak budeme premennú del zvyšovať, nebude mať zmysel zväčšovať ju nad hodnotu podiel=a/2, pretože číslo a nemôže deliť žiadne číslo, ktoré je väčšie ako a/2. Ďalej, nech del=3. Ak číslo del (del=3) nedelí číslo a, hranica delenia – n sa zníži na hodnotu a/3, pretože žiadne číslo väčšie ako a/3 nemôže deliť a bezo zvyšku. Z uvedeného nám vyplýva, že hranicu n môžeme určiť nasledovne: Pri každom delení si zapamätáme podiel. Ďalšie delenie robíme iba ak podiel>del. V algoritme použijeme ešte jednu premennú prvocislo. Táto premenná nám bude hovoriť, či je číslo prvočíslo alebo nie je. Na začiatku má hodnotu 1 – teda predpokladáme, že číslo je prvočíslo. V prípade, ak počas delenia zistíme, že nejaké číslo del delí a bezo zvyšku, premennej prvocislo priradíme hodnotu 0. Vyhlásime, že a nie je prvočíslo. | ||
| + | |||
| + | ; Ukážka: | ||
| + | *a=23 | ||
| + | *a del podiel | ||
| + | *23 / 2 = 11 zv 1 | ||
| + | *23 / 3 = 7 zv 2 | ||
| + | *23 / 4 = 5 zv 3 | ||
| + | *23 / 5 = 4 zv 3 del > podiel; koniec; a je prvočíslo, pretože ani jeden zvyšok po delení nebol 0 | ||
| + | *23 je prvočíslo. | ||
| + | |||
| + | |||
| + | [[Súbor:88 2 alg6.png|480px|none]] | ||
Aktuálna revízia z 19:15, 6. marec 2021
Riešené príklady
zdroj: Juraj Ďuďák, Zbierka úloh z algoritmizácie pre predmet Základy informatiky
ISBN: 978-80-8075-199-9
Obsah
Obsah
V tejto kapitole budú ukázaná tvorba jednoduchých vývojových diagramov. Budú ukázané základné prvky algoritmizácie úloh, použitie rozhodovania, opakovania istého počtu operácií. K zvládnutiu tejto kapitoly sa predpokladá znalosť grafických značiek použitých pri tvorbe vývojových diagramov.
Grafické značky vývojových diagramov
Medzi základné stavebné bloky vývojových diagramov (VD) patria bloky, ktoré reprezentujú
- začiatok / koniec VD
- vykonávací blok
- rozhodovací blok
- spojka
- vstup / výstup dát
- orientované spojnice blokov
Príklady
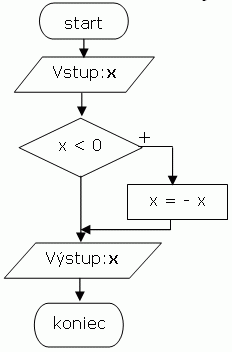
Absolútna hodnota
- Zadanie
- Vieme, že absolútna hodnota je definovaná ako vzdialenosť čísla od začiatku súradnicového systému (resp. od nuly). Nakreslite vývojový diagram, ktorý by znázorňoval výpočet absolútnej hodnoty.
- Analýza problému
- Pre absolútnu hodnotu reálnych čísel platí:
- abs(x) = x
- abs(-x) = x
Inak povedané, pre x>=0, je absolútna hodnota x rovná práve x, pre x<0 je absolútna hodnota x rovná -1*x. Teda, stačí nám zistiť, či je x menšie ako nula.
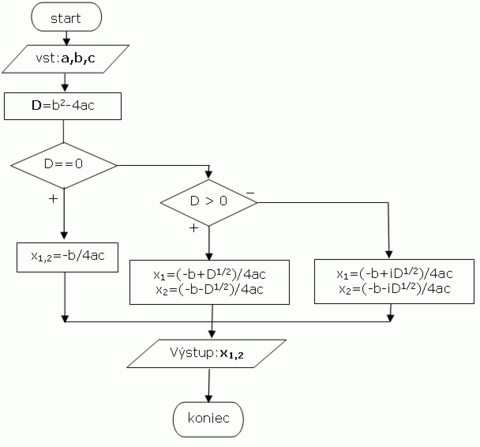
Kvadratická rovnica
- Zadanie
- Navrhnite algoritmus výpočtu koreňov kvadratickej rovnice ax2+bx+c=0. Vstupom do algoritmu budú koeficienty a, b, c, a výstupom budú korene kvadratickej rovnice x1,2.
- Analýza problému
- Riešenie tejto rovnice je známe, úlohou je tento problém znázorniť v podobe vývojového diagramu. Vieme, že kvadratická rovnica má dva korene (x1 a x2). Tieto korene môžu byť rôzne, alebo riešením je jeden dvojnásobný koreň. Toto zistíme pomocou výpočtu diskriminantu kvadratickej rovnice. Diskriminant je definovaný ako D=b2-4ac
Rozoberme si jednotlivé prípady riešenia.
- D>0 : Rovnica má dva korene: x1=(-b+D1/2)/2a, x2=(-b-D1/2)/2a
- D=0 : Rovnica má jeden dvojnásobný koreň: x1,2=-b/2a
- D<0 : Rovnica má riešenie na množine komplexných čísel:
Vieme, že i2=-1. (i je komplexná jednotka). Potom výpočet druhej odmocniny diskriminantu je (D)1/2=(i2 * (-D))1/2=i*(-D) ½ (poznámka: D<0). Teda korene kvadratickej rovnice budú x1=(-b+iD1/2)/2a, x2=(-b-iD1/2)/2a
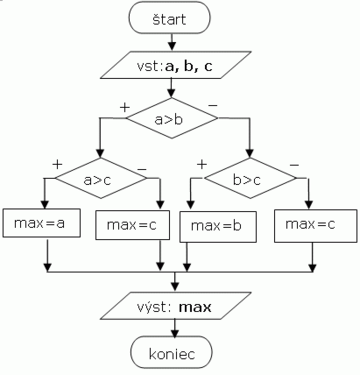
Maximum z 3 hodnôt
- Zadanie
- V predajni skrípt majú 3 skriptá, o ktoré máme záujem. Cena skrípt je a, b, c Sk. Navrhnite algoritmus, ktorý nájde najdrahšie skriptá; teda skriptá s maximálnou cenou.
- Analýza problému
- V prípade, ak máme zistiť maximálnu (alebo minimálnu) hodnotu z troch čísel, musíme každé číslo porovnať s každým iným číslom. Teda, spolu budeme robiť 3 porovnania (a<->b, a<->c, b<->c). Nemá zmysel porovnávať ab a ba, lebo toto sú totožné porovnania. Ak teda máme zistiť najväčšie číslo z a, b, c, môžeme postupovať napríklad nasledovne: Najskôr porovnáme : a>b. Ak toto platí, potom porovnáme a>c. V prípade ak aj toto platí, tak maximum je a. Keby platilo že: a>b a c>a, potom vieme, že maximum je c. Takto by sme mohli pokračovať ďalej.
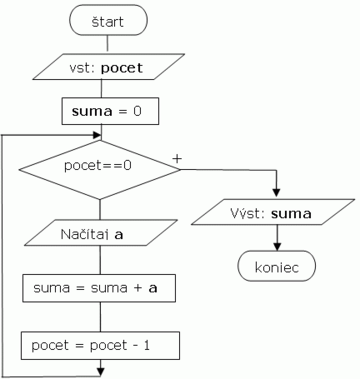
Opakované načítanie
- Zadanie
- Na faktúre je údaj o počte položiek a samotné položky (položka obsahuje o.i. aj cenu v Sk). Ak viete koľko je na faktúre položiek, navrhnite algoritmus, ktorý vypočíta celkovú sumu položiek faktúry. Prvý vstupný údaj bude číslo pocet, ktoré nám hovorí o počte nasledujúcich položiek. Následne sa načíta pocet položiek ( – celých čísel symbolizujúcim cenu položky). Navrhnite algoritmus, ktorý vypočíta výslednú sumu ceny všetkých položiek.
- Analýza problému
- V tomto prípade nikdy popredu nevieme, koľko budeme načítavať položiek. Tento údaj sa dozvieme až v momente, keď načítame prvý údaj. Úlohou bude teda navrhnúť algoritmus, ktorý by načítal požadovaný počet položiek (počet položiek môže byť od 0 až po ľubovoľne veľké konečné číslo). Na riešenie tohto problému využijeme cyklus. Tento cyklus sa bude opakovať toľkokrát, koľko položiek máme načítať. Pri každom opakovaní cyklu načítame jednu položku (položku označme ako premennú a) a jej hodnotu pripočítame k výslednej sume. Ďalším algoritmickým problémom je zabezpečiť, aby sa tento cyklus vykonával presne pocet krát. Tu využijeme prvý vstupný údaj pocet. Pri každej iterácii (opakovaní) cyklu sa hodnota premennej pocet zníži o 1. Cyklus budeme opakovať dovtedy, pokiaľ bude premenná pocet rôzna od nuly. Na výpočet súčtu všetkých položiek využijeme premennú suma, ktorú na začiatku vynulujeme (priradíme jej hodnotu 0).
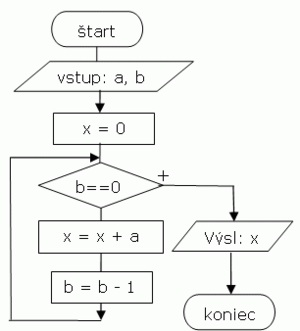
Násobenie
- Zadanie
- V počítačoch (na hardvérovej úrovni) sa operácia násobenia vykoná pomocou opakovaného sčítavania dvoch hodnôt. Vytvorte algoritmus, ktorý by násobil dve celé čísla pomocou opakovaného sčítavania.
- Analýza problému
- Na riešenie problému nemôžeme použiť operáciu násobenia (*), musíme použiť operáciu sčítavania (+). Zoberme si príklad: x=5*3. Tu budeme 3 krát pripočítame hodnotu 5 do premennej x, ktorú musíme najskôr vynulovať. Teda x=5+5+5=15. Vo všeobecnosti máme x=a*b=a+a+...+a : sčítavanie robíme b krát. Z uvedeného vyplýva, že nemôžeme pevne napísať, koľkokrát sa a pripočíta do premennej x. Tu bude vhodné využiť nejaký cyklus. V každom cykle sa do premennej x pripočíta hodnota a. Počet opakovaní cyklu je b. V každej iterácii cyklu hodnotu premennej b znížime o 1. Cyklus ukončíme, ak sa b=0.
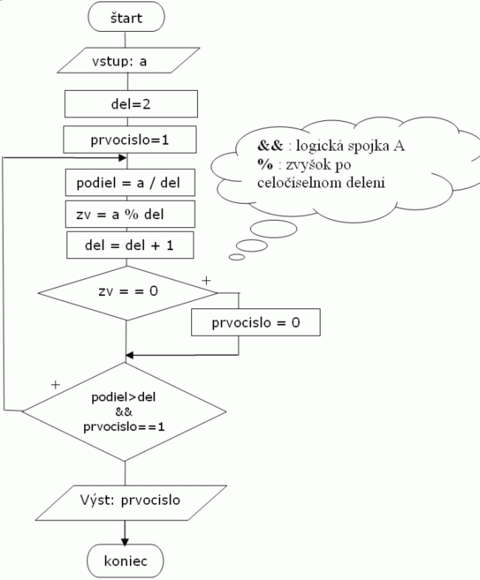
Prvočíslo
- Zadanie
- Navrhnite algoritmus, ktorý zistí, či zadané číslo a je prvočíslo.
- Analýza problému
- Prvočíslo je číslo, ktoré je delitelné iba číslom 1 a sebou samým. Pri testovaní čísla a na prvočíselnosť postupne celočíselne deliť číslo a číslami del=2, 3, ...n. Ak pri všetkých deleniach bude nejaký zvyšok (a sa nedá deliť číslom del), povieme že číslo a je prvočíslo. Ak v priebehu delenia zistíme, že a je delitené číslom del bezo zvyšku, algoritmus ukončíme, a povieme že a nie je prvočíslo. Ďalší problém je určiť, dokedy má zmysel zväčšovať deliteľ del. V predchádzajúcom texte sme del zvyšovali po hodnotu n. Úlohou je odhadnúť vhodné n. Pokúsme sa postupovať nasledovne: ako prvý deliteľ je del=2. Teda delíme a číslom del=2. Výsledok po tomto delení označme podiel. Ak budeme premennú del zvyšovať, nebude mať zmysel zväčšovať ju nad hodnotu podiel=a/2, pretože číslo a nemôže deliť žiadne číslo, ktoré je väčšie ako a/2. Ďalej, nech del=3. Ak číslo del (del=3) nedelí číslo a, hranica delenia – n sa zníži na hodnotu a/3, pretože žiadne číslo väčšie ako a/3 nemôže deliť a bezo zvyšku. Z uvedeného nám vyplýva, že hranicu n môžeme určiť nasledovne: Pri každom delení si zapamätáme podiel. Ďalšie delenie robíme iba ak podiel>del. V algoritme použijeme ešte jednu premennú prvocislo. Táto premenná nám bude hovoriť, či je číslo prvočíslo alebo nie je. Na začiatku má hodnotu 1 – teda predpokladáme, že číslo je prvočíslo. V prípade, ak počas delenia zistíme, že nejaké číslo del delí a bezo zvyšku, premennej prvocislo priradíme hodnotu 0. Vyhlásime, že a nie je prvočíslo.
- Ukážka
- a=23
- a del podiel
- 23 / 2 = 11 zv 1
- 23 / 3 = 7 zv 2
- 23 / 4 = 5 zv 3
- 23 / 5 = 4 zv 3 del > podiel; koniec; a je prvočíslo, pretože ani jeden zvyšok po delení nebol 0
- 23 je prvočíslo.