Booleova algebra: Rozdiel medzi revíziami

Z Kiwiki
Skočit na navigaci Skočit na vyhledávání
 
(5 medziľahlých úprav od 2 ďalších používateľov nie je zobrazených)
Riadok 1: Riadok 1:
 
[[Kategória:Študijné materiály]]
 
[[Kategória:Študijné materiály]]
 
[[Kategória:Informatika]]
 
[[Kategória:Informatika]]
 +
__TOC__
 
Slúži na matematický opis zákonov a pravidiel výrokovej logiky, ktorá rieši vzťahy medzi
 
Slúži na matematický opis zákonov a pravidiel výrokovej logiky, ktorá rieši vzťahy medzi
 
pravdivými a nepravdivými výrokmi. Pravdivému výroku prideľujeme logickú hodnotu 1
 
pravdivými a nepravdivými výrokmi. Pravdivému výroku prideľujeme logickú hodnotu 1
Riadok 26: Riadok 27:
 
| 1 || 1 || 1
 
| 1 || 1 || 1
 
|}
 
|}
 +
 +
'''Matematický príklad:''' Majme dva intervaly čísel (0,5) a <3,8). Aký bude výsledný interval konjunkcie týchto dvoch intervalov?
 +
 +
'''Riešenie''' Výsledný interval (0,5) ∧ <3,8) je <3,5).
  
 
[[Súbor:Boolova algebra AND.png|Logický súčin|300px]]
 
[[Súbor:Boolova algebra AND.png|Logický súčin|300px]]
Riadok 31: Riadok 36:
 
===Logický súčet (OR)===
 
===Logický súčet (OR)===
  
−
Odborne nazývaný '''logická disjunkcia'''. Označuje sa symbolom ∨ alebo + (v jazyku c/c++ je označená symbolom || pri podmienkach a symbolom | pri bitovom súčine), alebo sa používa pojem "alebo". Jeho výsledná hodnota Y je log. 1, ak aspoň jeden vstup A alebo B sú log. 1, inak je výsledkom log. 0.
+
Odborne nazývaný '''logická disjunkcia'''. Označuje sa symbolom ∨ alebo + (v jazyku c/c++ je označená symbolom || pri podmienkach, resp. logickom súčte a symbolom | pri bitovom súčte), alebo sa používa pojem "alebo". Jeho výsledná hodnota Y je log. 1, ak aspoň jeden vstup A alebo B sú log. 1, inak je výsledkom log. 0.
  
 
{| class="wikitable"
 
{| class="wikitable"
Riadok 45: Riadok 50:
 
| 1 || 1 || 1
 
| 1 || 1 || 1
 
|}
 
|}
 +
 +
'''Matematický príklad:''' Majme dva intervaly čísel (-1,2> a (3,8). Aký bude výsledný interval disjunkcie týchto dvoch intervalov?
 +
 +
'''Riešenie''' Výsledný interval (-1,2> ∨ (2,8) je <-1,8).
  
 
[[Súbor:Boolova algebra OR.png|300px|Logický súčet]]
 
[[Súbor:Boolova algebra OR.png|300px|Logický súčet]]
−
 
  
 
===Logická negácia (NOT)===
 
===Logická negácia (NOT)===
Riadok 172: Riadok 180:
 
==Príklad v jazyku C==
 
==Príklad v jazyku C==
  
−
Tento príklad zobrazuje, ako používať Booleovu algebru v jazyku C. Vstupy Booleovej algebry sú výrazy (A > B), (B > 2). Na začiatku programu je potrebné zadať dve čísla A a B, ktoré sa porovnávajú v daných výrazoch.
+
Tento príklad zobrazuje, ako používať Booleovu algebru v jazyku C. Vstupy Booleovej algebry sú výrazy ''(a > b)'', ''(b > 2)''. Na začiatku programu je potrebné zadať dve čísla ''a'' a ''b'', ktoré sa porovnávajú v daných výrazoch.
  
 
<source lang="c" line>
 
<source lang="c" line>
Riadok 178: Riadok 186:
 
int main(void)
 
int main(void)
 
{
 
{
−
int A = 0;
+
int a = 0;
−
int B = 0;
+
int b = 0;
 
printf("Zadaj cisla pre porovnanie: ");
 
printf("Zadaj cisla pre porovnanie: ");
−
scanf("%d %d", &A, &B); //načítanie dvoch čísiel
+
scanf("%d %d", &a, &b); //načítanie dvoch čísiel
  
−
//ak A > B a súčasne B > 2
+
//ak a > b a súčasne b > 2
−
if ((A > B) && (B > 2)) printf("(A > B) && (B > 2) je pravda\n");
+
if ((a > b) && (b > 2)) printf("(a > b) && (b > 2) je pravda\n");
−
else printf("(A > B) && (B > 2) je nepravda\n");
+
else printf("(a > b) && (b > 2) je nepravda\n");
  
−
//ak A > B alebo B > 2
+
//ak a > b alebo b > 2
−
if ((A > B) || (B > 2)) printf("(A > B) || (B > 2) je pravda\n");
+
if ((a > b) || (b > 2)) printf("(a > b) || (b > 2) je pravda\n");
−
else printf("(A > B) || (B > 2) je nepravda\n");
+
else printf("(a > b) || (b > 2) je nepravda\n");
  
−
//ak (A > B) negované
+
//ak (a > b) negované
−
if (!(A > B)) printf("!(A > B) je pravda\n");
+
if (!(a > b)) printf("!(a > b) je pravda\n");
−
else printf("!(A > B) je nepravda\n");
+
else printf("!(a > b) je nepravda\n");
  
 
return 0;
 
return 0;
Riadok 200: Riadok 208:
 
</source>
 
</source>
  
−
==Zdroje==
+
==Referencie==

Aktuálna revízia z 15:17, 26. máj 2020

Slúži na matematický opis zákonov a pravidiel výrokovej logiky, ktorá rieši vzťahy medzi pravdivými a nepravdivými výrokmi. Pravdivému výroku prideľujeme logickú hodnotu 1 a nepravidelnému výroku logickú hodnotu 0. Nositeľom elementárnej informácie o pravdivosti alebo nepravdivosti výroku je logická premenná, ktorá môže nadobúda dve hodnoty 0 a 1.[1]

Základy informatiky - jazyk C

Učebné texty

Booleova algebra

Algoritmus

Štruktúra kódu

Príkazy preprocesora

Dátové typy, premenné

Operátory

Vstupno/výstupné operácie

Podmienky

Cykly

Polia

Reťazce

Funkcie

Súbory

Štruktúry

Smerník (pointer)

Základné operácie

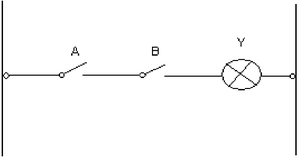
Logický súčin (AND)

Odborne nazývaný logická konjukcia. Označuje sa symbolom ∧ alebo . ,prípadne * (v jazyku c/c++ je označená symbolom && pri podmienkach a symbolom & pri bitovom súčine), alebo sa používa pojem "a súčasne". Jeho výsledná hodnota Y je log. 1, ak oba vstupy A aj B sú log. 1, inak je výsledkom log. 0. Pri počítaní Booleových rovníc má logický súčin prednosť pred logickým súčtom.

A B Y = A ∧ B
0 0 0
0 1 0
1 0 0
1 1 1

Matematický príklad: Majme dva intervaly čísel (0,5) a <3,8). Aký bude výsledný interval konjunkcie týchto dvoch intervalov?

Riešenie Výsledný interval (0,5) ∧ <3,8) je <3,5).

Logický súčin

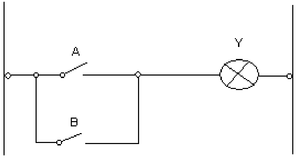
Logický súčet (OR)

Odborne nazývaný logická disjunkcia. Označuje sa symbolom ∨ alebo + (v jazyku c/c++ je označená symbolom || pri podmienkach, resp. logickom súčte a symbolom | pri bitovom súčte), alebo sa používa pojem "alebo". Jeho výsledná hodnota Y je log. 1, ak aspoň jeden vstup A alebo B sú log. 1, inak je výsledkom log. 0.

A B Y = A ∨ B
0 0 0
0 1 1
1 0 1
1 1 1

Matematický príklad: Majme dva intervaly čísel (-1,2> a (3,8). Aký bude výsledný interval disjunkcie týchto dvoch intervalov?

Riešenie Výsledný interval (-1,2> ∨ (2,8) je <-1,8).

Logický súčet

Logická negácia (NOT)

Označuje sa symbolom [math]\neg[/math] alebo apostrofom ' (v jazyku c/c++ je označená symbolom ! pri podmienkach a symbolom ~ pri bitovej negácii).. Jeho výsledná hodnota Y je log. 1, ak vstup A je log.0, inak je výsledkom log. 1.

A Y = [math]\neg[/math]A
0 1
1 0


Zložitejšie logické operácie

Negovaný logický súčin (NAND)

Dá sa vyjadriť pomocou základných logických operácií: Y = [math]\neg[/math](A ∧ B)

A B Y = [math]\neg[/math](A ∧ B)
0 0 1
0 1 1
1 0 1
1 1 0


Negovaný logický súčet (NOR)

Dá sa vyjadriť pomocou základných logických operácií: Y = [math]\neg[/math](A ∨ B)

A B Y = [math]\neg[/math](A ∨ B)
0 0 1
0 1 0
1 0 0
1 1 0


Exkluzívny logický súčet (XOR)

Odborne nazývaný exkluzívna disjunkcia. Označuje sa symbolom ⊕ (v jazyku c/c++ je označená symbolom != pri podmienkach a symbolom ^ pri bitovom súčine), alebo sa používa pojem "nerovná sa". Jeho výsledná hodnota Y je log. 1, ak sa vstup A nerovná vstupu B, inak je výsledkom log. 0. Dá sa vyjadriť pomocou základných logických operácií: A ⊕ B = A ∧ [math]\neg[/math]B ∨ [math]\neg[/math]A ∧ B

A B Y = A ⊕ B
0 0 0
0 1 1
1 0 1
1 1 0


Negovaný exkluzívny logický súčet (XNOR)

V jazyku c/c++ sa používa označenie == v podmienkach, alebo sa používa pojem "rovná sa". Dá sa vyjadriť pomocou základných logických operácií: Y = [math]\neg[/math](A ⊕ B)

A B Y = [math]\neg[/math](A ⊕ B)
0 0 1
0 1 0
1 0 0
1 1 1


Zákony Booleovej algebry

Pre zjednodušenie práce s rovnicami v Booleovej algebre je možné používať tieto zákony:

Zákon súčtu Zákon súčinu
Zákon idempotencie A ∨ A = A A ∧ A = A
Zákon absorpcie A ∨ A ∧ B = A A ∧ (A ∨ B) = A
Zákon absorpcie negácie A ∨ ([math]\neg[/math]A ∧ B) = A ∨ B A ∧ ([math]\neg[/math]A ∨ B) = A ∧ B
Komutačný zákon A ∨ B = B ∨ A A ∧ B = B ∧ A
Asociatívny zákon A ∨ (B ∨ C) = (A ∨ B) ∨ C A ∧ (B ∧ C) = (A ∧ B) ∧ C
Distributívny zákon A ∨ (B ∧ C) = (A ∨ B) ∧ (A ∨ C) A ∧ (B ∨ C) = A ∧ B ∨ A ∧ C
Neutrálnosť nuly a jednotky A ∨ 0 = A A ∧ 1 = A
Agresívnosť nuly a jednotky A ∨ 1 = 1 A ∧ 0 = 0
Zákon vylúčeného tretieho A ∨ [math]\neg[/math]A = 1 A ∧ [math]\neg[/math]A = 0
Zákon negácie [math]\neg[/math]0 = 1 [math]\neg[/math]1 = 0
Zákon dvojitej negácie [math]\neg[/math][math]\neg[/math]A = A
De Morganove zákony [math]\neg[/math](A ∨ B) = [math]\neg[/math]A ∧ [math]\neg[/math]B [math]\neg[/math](A ∧ B) = [math]\neg[/math]A ∨ [math]\neg[/math]B

[2]

Príklad v jazyku C

Tento príklad zobrazuje, ako používať Booleovu algebru v jazyku C. Vstupy Booleovej algebry sú výrazy (a > b), (b > 2). Na začiatku programu je potrebné zadať dve čísla a a b, ktoré sa porovnávajú v daných výrazoch. 

 1 #include<stdio.h>
 2 int main(void)
 3 {
 4 	int a = 0;
 5 	int b = 0;
 6 	printf("Zadaj cisla pre porovnanie: ");
 7 	scanf("%d %d", &a, &b); //načítanie dvoch čísiel
 8 
 9 	//ak a > b a súčasne b > 2
10 	if ((a > b) && (b > 2)) printf("(a > b) && (b > 2) je pravda\n");
11 	else printf("(a > b) && (b > 2) je nepravda\n");
12 
13 	//ak a > b alebo b > 2
14 	if ((a > b) || (b > 2)) printf("(a > b) || (b > 2) je pravda\n");
15 	else printf("(a > b) || (b > 2) je nepravda\n");
16 
17 	//ak (a > b) negované
18 	if (!(a > b)) printf("!(a > b) je pravda\n");
19 	else printf("!(a > b) je nepravda\n");
20 
21 	return 0;
22 }

Referencie

  1. ↑ https://encyklopediapoznania.sk/data/eknihy/matematika/boolova_algebra.pdf
  2. ↑ http://www.et-pocitacovesystemy.wz.cz/cislicova_technika/logfce/bool_algebra/booleova_algebra.html
Zdroj: „http://www.kiwiki.info/index.php?title=Booleova_algebra&oldid=12698“