Filtre/Narrow band pass filter: Rozdiel medzi revíziami
Skočit na navigaci
Skočit na vyhledávání
| Riadok 38: | Riadok 38: | ||
=== Výpočet filtra === | === Výpočet filtra === | ||
| + | |||
| + | <source lang="python" line> | ||
| + | from scipy import * | ||
| + | from pylab import * | ||
| + | |||
| + | R1=1928 | ||
| + | R2=101 | ||
| + | R3=36644 | ||
| + | R4=R1 | ||
| + | |||
| + | f=4000 | ||
| + | C1=20.63e-9 | ||
| + | C2=C1 | ||
| + | |||
| + | Y1=1.0/R1 | ||
| + | Y2=1.0/R2 | ||
| + | Y34=1.0/(R3+R4) | ||
| + | |||
| + | ampl=[] | ||
| + | freq=[] | ||
| + | |||
| + | for f in range(1000, 10000, 10): | ||
| + | p=(2*pi*f)*1.0j | ||
| + | K=-p*C2*Y1/(p*p*C1*C2 -( -(Y34)*( p*(C1+C2)+Y1+Y2 ) ) ) | ||
| + | |||
| + | ampl.append(abs(K)) | ||
| + | freq.append(f) | ||
| + | |||
| + | plot(freq,ampl) | ||
| + | grid() | ||
| + | show() | ||
| + | </source> | ||
=== Odkazy a literatúra === | === Odkazy a literatúra === | ||
<references/> | <references/> | ||
Verzia zo dňa a času 21:36, 27. máj 2013
Zapojenie filtra
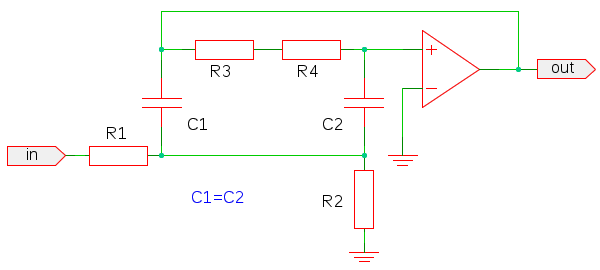
|
| Zapojenie filtra |
Analýza filtra
Analýzu vlastností filtra prevedieme pomocou zovšeobecnenej metódy uzlových napätí. [1]. Admitancie prvkov sú definované ako
- [math] Y_1=1/R_1 [/math]
- [math] Y_2=1/R_2 [/math]
- [math] Y_{34}=1/(R_3+R_4) [/math]
Admitančná matica filtra pri použití ideálneho operačného zosilňovača má tvar
- [math] \begin{bmatrix} Y_1 & -Y_1 & 0 & 0 \\ -Y_1 & p(C_1+C_2)+Y_1+Y_2 & -pC_2 & -pC_1 \\ 0 & -pC_2 & -Y_{34} & 0 \\ 0 & 0 & 1 & 0 \\ \end{bmatrix} [/math]
Komplexná napäťová prenosová funkcia filtra je určená pomerom subdeterminantov
- [math] K(p) = \frac{D_{14}}{D_{11}}=(-1)^{(1+4)} \frac{p C_2 Y_1}{p^2 C_1 C_2 + Y_{34}*(Y_1+Y_2+p C_1+ p C_2 ) } [/math]
Výpočet filtra
1 from scipy import *
2 from pylab import *
3
4 R1=1928
5 R2=101
6 R3=36644
7 R4=R1
8
9 f=4000
10 C1=20.63e-9
11 C2=C1
12
13 Y1=1.0/R1
14 Y2=1.0/R2
15 Y34=1.0/(R3+R4)
16
17 ampl=[]
18 freq=[]
19
20 for f in range(1000, 10000, 10):
21 p=(2*pi*f)*1.0j
22 K=-p*C2*Y1/(p*p*C1*C2 -( -(Y34)*( p*(C1+C2)+Y1+Y2 ) ) )
23
24 ampl.append(abs(K))
25 freq.append(f)
26
27 plot(freq,ampl)
28 grid()
29 show()