Generátor s komparátorom: Rozdiel medzi revíziami
d |
|||
| (3 medziľahlé úpravy od jedného ďalšieho používateľa nie sú zobrazené) | |||
| Riadok 1: | Riadok 1: | ||
__NOTOC__ | __NOTOC__ | ||
[[Category:Simulácie a modelovanie]] | [[Category:Simulácie a modelovanie]] | ||
| + | {{Simulacia_modelovanie_3|7}} | ||
Generátor pravouhlého priebehu pozostáva z invertujúceho Schmittovho klopného obvodu <ref>http://en.wikipedia.org/wiki/Schmitt_trigger</ref> tvoreného komponentami [[Model-Komparátor | XCOMP]], R<sub>3</sub>, R<sub>4</sub> a dolnofrekvenčného filtra R<sub>1</sub>, C<sub>1</sub>. | Generátor pravouhlého priebehu pozostáva z invertujúceho Schmittovho klopného obvodu <ref>http://en.wikipedia.org/wiki/Schmitt_trigger</ref> tvoreného komponentami [[Model-Komparátor | XCOMP]], R<sub>3</sub>, R<sub>4</sub> a dolnofrekvenčného filtra R<sub>1</sub>, C<sub>1</sub>. | ||
| + | |||
| + | <center> | ||
| + | {|class="wikitable" | ||
| + | | align="center" width=500 | [[Súbor:0558_comp.png | 500px]] | ||
| + | |- | ||
| + | | align="center" width=500 | '''Zapojenie obvodu''' | ||
| + | |} | ||
| + | </center> | ||
Kondenzátor sa nabíja cez odpor R<sub>1</sub> kladným napätím z výstupu komparátora. Keď potenciál v uzle IN- dosiahne kladnú komparačnú hodnotu Schmittovho klopného obvodu, tento sa skokom preklopí do opačnej zápornej polarity a v tomto stave zostane po dobu, kým napätie na uzle IN- nedosiahne zápornú komparačnú hodnotu. Obvod preklopí späť do kladnej polarity a celý cyklus sa opakuje. | Kondenzátor sa nabíja cez odpor R<sub>1</sub> kladným napätím z výstupu komparátora. Keď potenciál v uzle IN- dosiahne kladnú komparačnú hodnotu Schmittovho klopného obvodu, tento sa skokom preklopí do opačnej zápornej polarity a v tomto stave zostane po dobu, kým napätie na uzle IN- nedosiahne zápornú komparačnú hodnotu. Obvod preklopí späť do kladnej polarity a celý cyklus sa opakuje. | ||
| Riadok 8: | Riadok 17: | ||
:<math> | :<math> | ||
\begin{align} | \begin{align} | ||
| − | + | U_{ON} &= - \alpha \, U_{OUT} \\ | |
| − | + | U_{OFF} &= \alpha \, U_{OUT} | |
| − | \alpha &= \frac {R_1} {R_1 + | + | \end{align} |
| + | </math> | ||
| + | |||
| + | Pre koeficient <math>\alpha</math> platí | ||
| + | |||
| + | :<math> | ||
| + | \alpha = \frac {R_1} {R_1 + R_2} | ||
| + | </math> | ||
| + | |||
| + | Pre napätie U<sub>C</sub> na kondenzátore platí diferenciálna rovnica | ||
| + | |||
| + | :<math> | ||
| + | \frac {d U_C} {dt} = \pm \frac {U_{OUT} - U_C} {R_1 C_1} | ||
| + | </math> | ||
| + | |||
| + | |||
| + | Pri riešení diferenciálnej rovnice predpokladajme počiatočnú podmienku, že kondenzátor sa začína nabíjať z dolnej komparačnej úrovne U<sub>ON</sub> a celkové napätie na kondenzátore potom bude U<sub>OUT</sub>+U<sub>ON</sub>. Riešenie diferenciálnej má potom tvar | ||
| + | |||
| + | :<math> | ||
| + | \begin{align} | ||
| + | U_{C}(t) &= \left( U_{OUT} + \alpha U_{OUT} \right) \left( 1 - e^{- \frac {t} {R_1 C_1} } \right ) - \alpha U_{OUT} \\ | ||
| + | &= U_{OUT} \big[ 1 - \left( 1 + \alpha \right) e^{- \frac {t} {R_1 C_1} } \big] | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |||
| + | |||
| + | Dobu nabíjania kondenzátora z dolnej komparačnej úrovne do hornej získame riešením rovnice nabíjania kondenzátora pre neznámu hodnotu t<sub>1</sub> nasledujúcimi úpravami | ||
| + | |||
| + | :<math> | ||
| + | \begin{align} | ||
| + | U_{OFF} &= U_{OUT} \big[ 1 - \left( 1 + \alpha \right) e^{- \frac {t_1} {R_1 C_1} } \big] \\ | ||
| + | |||
| + | \alpha U_{OUT} &= U_{OUT} \big[ 1 - \left( 1 + \alpha \right) e^{- \frac {t_1} {R_1 C_1} } \big] \\ | ||
| + | |||
| + | (1 -\alpha ) &= ( 1 + \alpha ) e^{- \frac {t} {R_1 C_1} } \\ | ||
| + | |||
| + | t_1 &= R_1 C_1 ln \left( \frac { 1 + \alpha } {1 -\alpha } \right) \\ | ||
| + | |||
| + | t_1 &= R_1 C_1 ln \left( 1 + \frac { 2 R_4 } { R_3 } \right) | ||
| + | |||
\end{align} | \end{align} | ||
</math> | </math> | ||
| − | < | + | Perióda kmitov generátora je potom rovná |
| − | { | + | |
| − | + | :<math> | |
| − | + | T = 2 t_1 = 2 R_1 C_1 ln \left( 1 + \frac { 2 R_4 } { R_3 } \right) | |
| − | + | </math> | |
| − | + | ||
| − | </ | + | Ak zvolíme hodnoty R<sub>3</sub>=R<sub>4</sub>, pre periódu kmitov platí |
| − | + | ||
| + | :<math> | ||
| + | T = 2 ln(3) \, R_1 C_1 = 2.2 R_1 C_1 | ||
| + | </math> | ||
| + | |||
| + | |||
| + | Simulované priebehy v uzloch IN+, IN- a na výstupe OUT generátora sú zobrazené na nasledujúcom obrázku. Použitie parametra UIC pri simulácii okrem stanovenia počiatočných podmienok pre zobrazenie nie je potrebné, obvod nemá metastabilný stav. | ||
| + | |||
<center> | <center> | ||
{|class="wikitable" | {|class="wikitable" | ||
Aktuálna revízia z 22:06, 22. marec 2013
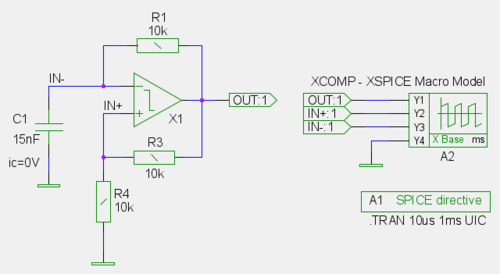
Generátor pravouhlého priebehu pozostáva z invertujúceho Schmittovho klopného obvodu [1] tvoreného komponentami XCOMP, R3, R4 a dolnofrekvenčného filtra R1, C1.
|
| Zapojenie obvodu |
Kondenzátor sa nabíja cez odpor R1 kladným napätím z výstupu komparátora. Keď potenciál v uzle IN- dosiahne kladnú komparačnú hodnotu Schmittovho klopného obvodu, tento sa skokom preklopí do opačnej zápornej polarity a v tomto stave zostane po dobu, kým napätie na uzle IN- nedosiahne zápornú komparačnú hodnotu. Obvod preklopí späť do kladnej polarity a celý cyklus sa opakuje.
Pre komparačné hodnoty Schmittovho klopného obvodu platí
- [math] \begin{align} U_{ON} &= - \alpha \, U_{OUT} \\ U_{OFF} &= \alpha \, U_{OUT} \end{align} [/math]
Pre koeficient [math]\alpha[/math] platí
- [math] \alpha = \frac {R_1} {R_1 + R_2} [/math]
Pre napätie UC na kondenzátore platí diferenciálna rovnica
- [math] \frac {d U_C} {dt} = \pm \frac {U_{OUT} - U_C} {R_1 C_1} [/math]
Pri riešení diferenciálnej rovnice predpokladajme počiatočnú podmienku, že kondenzátor sa začína nabíjať z dolnej komparačnej úrovne UON a celkové napätie na kondenzátore potom bude UOUT+UON. Riešenie diferenciálnej má potom tvar
- [math] \begin{align} U_{C}(t) &= \left( U_{OUT} + \alpha U_{OUT} \right) \left( 1 - e^{- \frac {t} {R_1 C_1} } \right ) - \alpha U_{OUT} \\ &= U_{OUT} \big[ 1 - \left( 1 + \alpha \right) e^{- \frac {t} {R_1 C_1} } \big] \end{align} [/math]
Dobu nabíjania kondenzátora z dolnej komparačnej úrovne do hornej získame riešením rovnice nabíjania kondenzátora pre neznámu hodnotu t1 nasledujúcimi úpravami
- [math] \begin{align} U_{OFF} &= U_{OUT} \big[ 1 - \left( 1 + \alpha \right) e^{- \frac {t_1} {R_1 C_1} } \big] \\ \alpha U_{OUT} &= U_{OUT} \big[ 1 - \left( 1 + \alpha \right) e^{- \frac {t_1} {R_1 C_1} } \big] \\ (1 -\alpha ) &= ( 1 + \alpha ) e^{- \frac {t} {R_1 C_1} } \\ t_1 &= R_1 C_1 ln \left( \frac { 1 + \alpha } {1 -\alpha } \right) \\ t_1 &= R_1 C_1 ln \left( 1 + \frac { 2 R_4 } { R_3 } \right) \end{align} [/math]
Perióda kmitov generátora je potom rovná
- [math] T = 2 t_1 = 2 R_1 C_1 ln \left( 1 + \frac { 2 R_4 } { R_3 } \right) [/math]
Ak zvolíme hodnoty R3=R4, pre periódu kmitov platí
- [math] T = 2 ln(3) \, R_1 C_1 = 2.2 R_1 C_1 [/math]
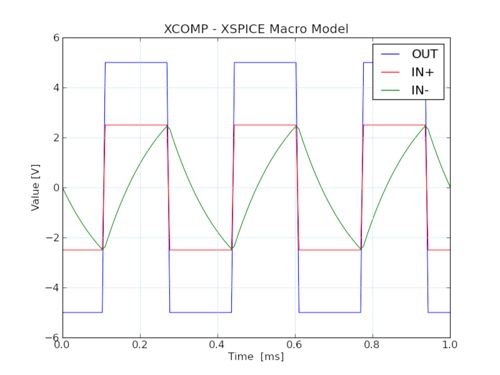
Simulované priebehy v uzloch IN+, IN- a na výstupe OUT generátora sú zobrazené na nasledujúcom obrázku. Použitie parametra UIC pri simulácii okrem stanovenia počiatočných podmienok pre zobrazenie nie je potrebné, obvod nemá metastabilný stav.
|
| Výsledok simulácie |