Vyhodnotenie simulácie vlastností generátorov prevádzkových tokov
| 1. | WDM optické siete |
| 2. | Sieť OBS |
| 3. | Simulačné prostredie NCTUns |
| 4. | Simulácia v NCTUns |
| 5. | Vyhodnotenie simulácie vlastností generátorov prevádzkových tokov
|
Obsah
Vyhodnotenie simulácií spracujem pomocou metódy Chi Square Test - Test Dobrej zhody. Spracovanie dát bude prebiehať v programoch MS Excel 2007 a Statistica 7.
V programe MS Excel 2007 vytvorím akúsi predprípravu dát na finálne spracovanie. Dáta vygenerované do výstupného logu sú totiž veľmi rozsiahle (rádovo desať tisíce záznamov ) a príliš „surové“. Z pohľadu spracovania sú dôležité uzly 10 a 6 (viď Obrázok 17: Topologia pre simuláciu), nakoľko práve medzi týmito dvoma uzlami je zaujímavý charakter sieťovej prevádzky. V programe MS Excel 2007 pospájam polia podľa packet trace format, pomocou jednoduchých vzorcov. Následne vyfiltrujem dáta len pre sieťovú prevádzku z uzla 10 do uzla 6.
Vyfiltrované dáta spracujem v prostredí Statictica 7. Zostrojím histogramy pre všetky simulácie, až následne dáta z histogramov budem môcť použiť do Testu Dobrej zhody.
Chi Square Test – Test Dobrej Zhody
Chi-kvadrát test dobrej zhody testuje nulovú štatistickú hypotézu, ktorá tvrdí, že početnosti v jednotlivých kategóriách sa rovnajú očakávaným (teoretickým) početnostiam.
Ak P - hodnota je nižšia ako zvolená hladina významnosti (tradične 5 % = 0,05, prípadne 1 % alebo 0,1 %), nulová hypotéza sa zamietne. Znamená to, že rozdiel medzi početnosťami zistenými vo vzorke a očakávanými početnosťami je príliš veľký na to, aby bol iba dôsledkom náhodného výberu, teda je štatisticky významný.
Ak je P - hodnota rovná alebo vyššia ako zvolená hladina významnosti, nulovú hypotézu nemožno zamietnuť. Znamená to, že rozdiel medzi početnosťami zistenými vo vzorke a očakávanými početnosťami môže byť dôsledkom náhodného výberu, teda nie je štatisticky významný.
Pre použitie testu sa vyžaduje splnenie nasledujúcich podmienok:
- Celkový počet pozorovaných početností n ≥ 10
- Počet kategórií c ≥ 3
- Všetky očakávané hodnoty eij ≥ 0,25 [7]
Často používame tento test pre overenie predpokladu, že rozdelenie pravdepodobnosti veličiny P je určitého typu, napríklad normálne rozdelenie, Poissonové rozdelenie, Exponenciálne apod. V prípade, že nulová hypotéza špecifikuje iba typ pravdepodobnostného rozdelenia, ale nie hodnoty parametrov rozdelenia, musia byť parametre dopredu z výberu odhadnuté. Na každý takýto odhad sa počet stupňov voľnosti testovanej štatistiky znižuje o jedna. [8]
Vzťahy pre výpočet nulovej hypotézy
Testovanú štatistiku X2 je možné vyjadriť nasledovne:
|
[math]{{X}^{2}}=\underset{i=1}{\overset{k}{\mathop \sum }}\,\frac{{{\left( {{n}_{i}}-n{{\pi }_{i}} \right)}^{2}}}{n\pi i}[/math] |
(1) |
Kde premenné funkcie sú:
- [math]n_i[/math] – pozorovaná početnosť
- [math]n{\pi }_{i}[/math] – očakávaná početnosť
- k – počet triednych intervalov.
Pomer [math]n_i[/math] voči n je možné vyjadriť:
[math]\frac{n_i}{n}[/math] - pomer relatívnej početnosti
a
[math]{\pi }_{i}[/math] – hypotetická pravdepodobnosť
Vyjadrenú testovanú štatistiku je následne nutné porovnať s kritickou hodnotou, ktorá je rovná kvantilu:
|
[math]X_{1-\alpha ~}^{2}(df)[/math] |
(2) |
Rozdelenie [math]X^2[/math]:
|
[math]df=k-m-1 [/math] |
(3) |
Kde premenné sú:
- df – počet stupňov voľnosti
- m – počet parametrov
Vzťah 3 platí len pre situáciu, kde nulovú hypotézu uplatňujeme na overenie pravdepodobnosti, že určité rozdelenie je daného typu, inak platí nasledovné:
|
[math]df=k-1[/math] |
(4) |
Pre určenie kritickej hodnoty použijem tabuľku v Príloha B. V tabuľke je spracovaný výpočet kritickej chyby. Stĺpce tabuľky tvoria hladiny významnosti a riadky stupne voľnosti štatistického súboru. [8]
Vzťažné - očakávané dáta sú v mojom prípade dáta vygenerované programom MS Excel 2007 podľa daného rozdelenia. Pozorované dáta sú vygenerované simulačným prostredím NCTUns. Pozorované dáta boli generované na základe mnou vytvorených skriptov. Nasleduje 6 vybratých simulácií rozdelených do 3 scenárov.
Scenár 1: Exponenciálne rozdelenie
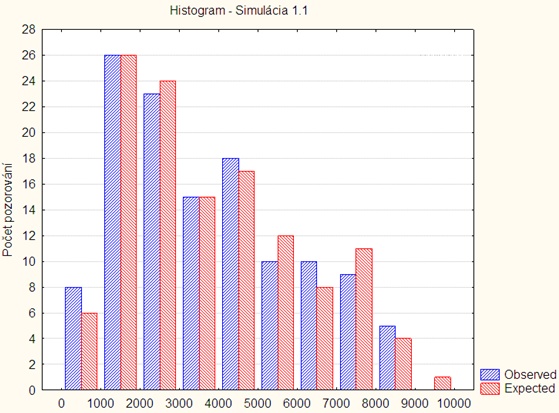
Simulácia 1.1
Vstupný skript:
type: udp
start_time: 1
on-off: 200
on: time: 600 const 0.01 length: exponential 800 50 1000
Histogram:
Popis legendy:
- Obseved – ni
- Expected - [math]n{\pi}i[/math]
Poznámka: Platí pre všetky simulácie.
Tabuľka spracovania:
| i | ni | nπi | x2i |
| 1 | 8 | 6 | 0,667 |
| 2 | 26 | 26 | 0,000 |
| 3 | 23 | 24 | 0,042 |
| 4 | 15 | 15 | 0,000 |
| 5 | 18 | 17 | 0,059 |
| 6 | 10 | 12 | 0,333 |
| 7 | 10 | 8 | 0,500 |
| 8 | 9 | 11 | 0,364 |
| 9 | 5 | 4 | 0,250 |
| 10 | 0 | 1 | 1,000 |
- df=k-m-1=8
- x2=3,214
- α=15,510
- x2 < α
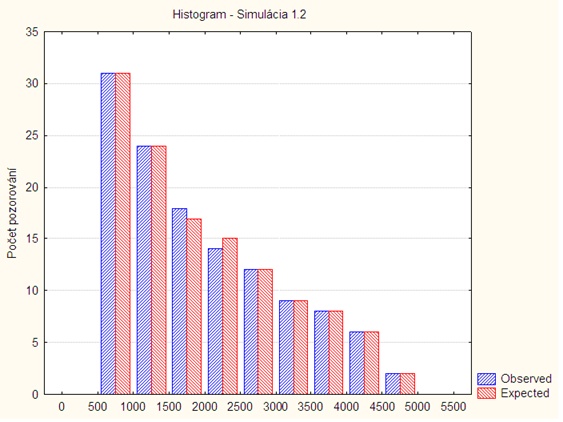
Simulácia 1.2
Vstupný skript:
type: udp
start_time: 1
on-off: 200
on: time: 600 const 0.01 length: exponential 100 10 800
Histogram:
Tabuľka spracovania:
| i | ni | nπi | x2i |
| 1 | 31 | 31 | 0,000 |
| 2 | 24 | 24 | 0,000 |
| 3 | 18 | 17 | 0,059 |
| 4 | 14 | 15 | 0,067 |
| 5 | 13 | 13 | 0,000 |
| 6 | 9 | 9 | 0,000 |
| 7 | 8 | 8 | 0,000 |
| 8 | 7 | 7 | 0,000 |
| 9 | 3 | 3 | 0,000 |
- df=k-m-1=7
- x2=0,125
- α=14,07
- x2 < α
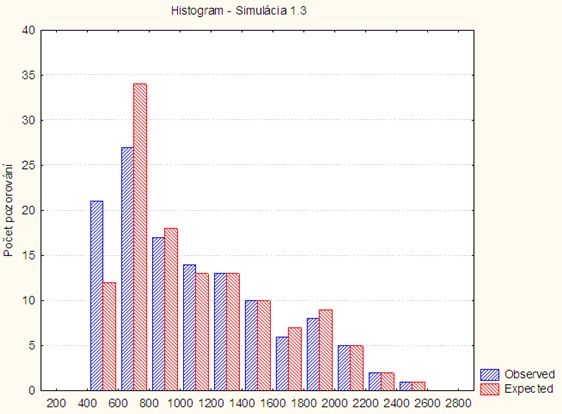
Simulácia 1.3
Vstupný skript:
type: udp
start_time: 1
on-off: 200
on: time: 600 const 0.01 length: exponential 100 10 250
Histogram:
Tabuľka spracovania:
| i | ni | nπi | x2i |
| 1 | 21 | 13 | 4,923 |
| 2 | 27 | 34 | 1,441 |
| 3 | 17 | 18 | 0,056 |
| 4 | 14 | 13 | 0,077 |
| 5 | 13 | 13 | 0,000 |
| 6 | 10 | 10 | 0,000 |
| 7 | 6 | 7 | 0,143 |
| 8 | 8 | 9 | 0,111 |
| 9 | 5 | 5 | 0,000 |
| 10 | 2 | 2 | 0,000 |
| 11 | 1 | 1 | 0,000 |
- df=k-m-1=9
- x2=6,751
- α=16,920
- x2 < α
Scenár 2: Konštantné rozdelenie
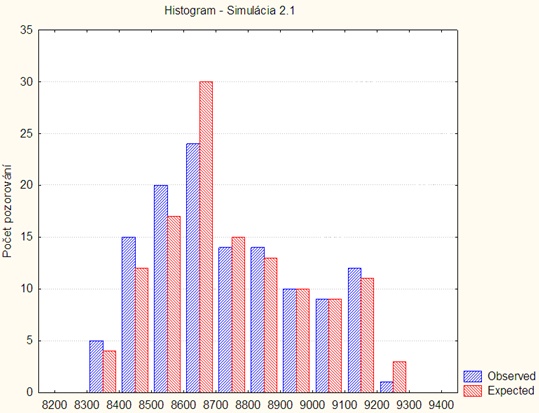
Simulácia 2.1
Vstupný skript:
type: udp
start_time: 1
on-off: 200
on: time: 600 const 0.01 length:const 1000
Histogram:
Tabuľka spracovania:
| i | ni | nπi | x2i |
| 1 | 5 | 4 | 0,250 |
| 2 | 15 | 12 | 0,750 |
| 3 | 20 | 17 | 0,529 |
| 4 | 24 | 30 | 1,200 |
| 5 | 14 | 15 | 0,067 |
| 6 | 14 | 13 | 0,077 |
| 7 | 10 | 10 | 0,000 |
| 8 | 9 | 9 | 0,000 |
| 9 | 12 | 11 | 0,091 |
| 10 | 1 | 3 | 1,333 |
- df=k-m-1=8
- x2=4,279
- α=15,510
- x2 < α
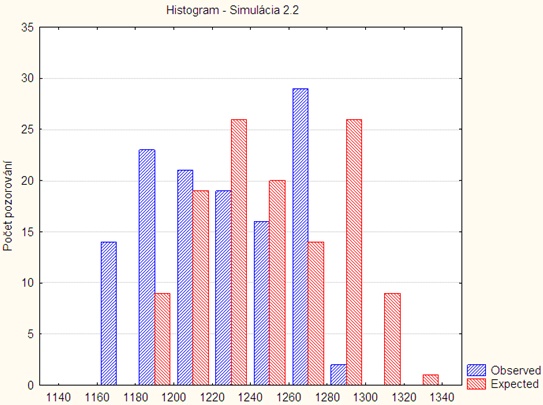
Simulácia 2.2
Vstupný skript:
type: udp
start_time: 1
on-off: 200
on: time: 600 const 0.01 length: const 100
Histogram:
Tabuľka spracovania:
| i | ni | nπi | x2i |
| 1 | 14 | 0 | - |
| 2 | 23 | 9 | 21,778 |
| 3 | 21 | 19 | 0,211 |
| 4 | 19 | 26 | 1,885 |
| 5 | 16 | 20 | 0,800 |
| 6 | 29 | 14 | 16,071 |
| 7 | 2 | 26 | 22,154 |
| 8 | 0 | 9 | 9,000 |
| 9 | 0 | 1 | 1,000 |
- df=k-m-1=7
- x2=72,898
- α=14,07
- x2 > α
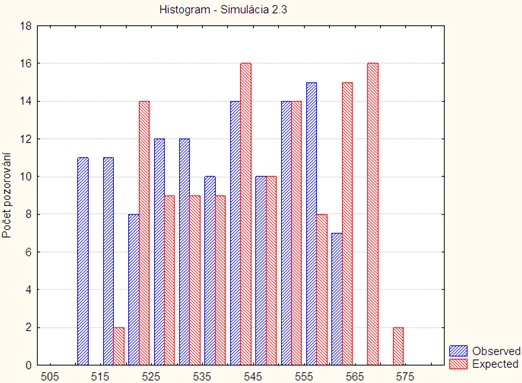
Simulácia 2.3
Vstupný skript:
type: udp
start_time: 1
on-off: 200
on: time: 600 const 0.01 length: const 10
Histogram:
Tabuľka spracovania:
| i | ni | nπi | x2i |
| 1 | 13 | 0 | - |
| 2 | 13 | 2 | 60,500 |
| 3 | 8 | 14 | 2,571 |
| 4 | 12 | 9 | 1,000 |
| 5 | 12 | 9 | 1,000 |
| 6 | 10 | 9 | 0,111 |
| 7 | 14 | 16 | 0,250 |
| 8 | 10 | 10 | 0,000 |
| 9 | 14 | 14 | 0,000 |
| 10 | 15 | 8 | 6,125 |
| 11 | 7 | 15 | 4,267 |
| 12 | 0 | 16 | 16,000 |
| 13 | 0 | 2 | 2,000 |
- df=k-m-1=11
- x2=93,824
- α=19,68
- x2 > α
Scenár 3: Rovnomerné rozdelenie
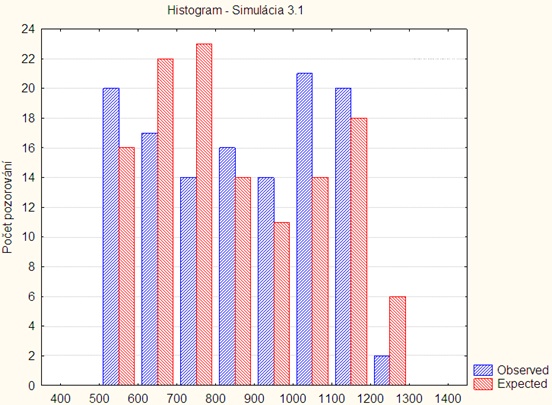
Simulácia 3.1
Vstupný skript:
type: udp
start_time: 1
on-off: 200
on: time: 600 const 0.01 length: uniform 10 100
Histogram:
Tabuľka spracovania:
| i | ni | nπi | x2i |
| 1 | 20 | 16 | 1,000 |
| 2 | 17 | 22 | 1,136 |
| 3 | 14 | 23 | 3,522 |
| 4 | 16 | 14 | 0,286 |
| 5 | 14 | 11 | 0,818 |
| 6 | 21 | 14 | 3,500 |
| 7 | 20 | 18 | 0,222 |
| 8 | 2 | 6 | 2,667 |
- df=k-m-1=6
- x2=13,151
- α=12,59
- x2 > α
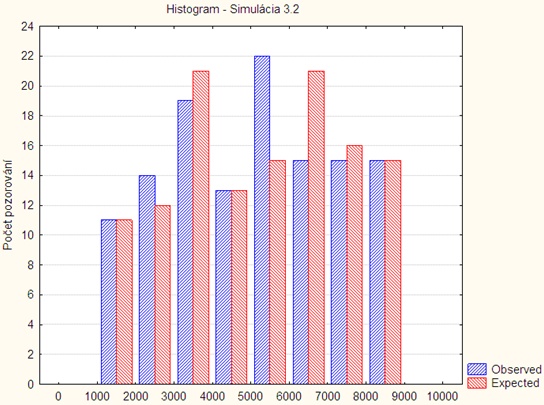
Simulácia 3.2
Vstupný skript:
type: udp
start_time: 1
on-off: 200
on: time: 600 const 0.01 length: uniform 100 1000
Histogram:
Tabuľka spracovania:
| i | ni | nπi | x2i |
| 1 | 11 | 11 | 0,000 |
| 2 | 14 | 12 | 0,333 |
| 3 | 17 | 21 | 0,762 |
| 4 | 13 | 13 | 0,000 |
| 5 | 22 | 15 | 3,267 |
| 6 | 15 | 21 | 1,714 |
| 7 | 15 | 16 | 0,063 |
| 8 | 15 | 15 | 0,000 |
- df=k-m-1=6
- x2=6,139
- α=12,590
- x2 < α
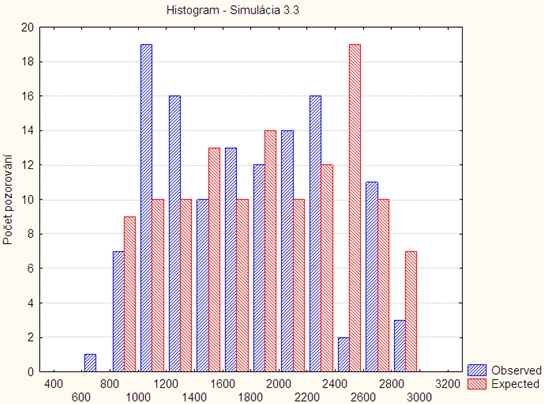
Simulácia 3.3
Vstupný skript:
type: udp
start_time: 1
on-off: 200
on: time: 600 const 0.01 length: uniform 50 300
Histogram:
Tabuľka spracovania:
| i | ni | nπi | x2i |
| 1 | 3 | 0 | - |
| 2 | 7 | 9 | 0,444 |
| 3 | 19 | 10 | 8,100 |
| 4 | 16 | 10 | 3,600 |
| 5 | 10 | 13 | 0,692 |
| 6 | 13 | 10 | 0,900 |
| 7 | 12 | 14 | 0,286 |
| 8 | 14 | 10 | 1,600 |
| 9 | 16 | 12 | 1,333 |
| 10 | 2 | 19 | 15,211 |
| 11 | 11 | 10 | 0,100 |
| 12 | 3 | 7 | 2,286 |
- df=k-m-1=10
- x2=34,552
- α=18,31
- x2 > α
Zhrnutie
Počet simulácií, kde testovaný štatistický súbor vyšiel menší ako kritická hodnota je 5 a naopak počet simulácií kde testovaný štatistický súbor vyšiel väčší ako kritická hodnota je 4. Zaujímavé je aj členenie správnych výsledkov, pri exponenciálnom rozdelení vyšli všetky výsledky menšie ako kritická hodnota a naopak pri rovnomernom rozdelení vyšla nižšia iba jedna hodnota. Pri zvažovaní a tvorbe záveru je nutné brať na zreteľ i rušivé vplyvy na vyhodnotenie. Za rušivý vplyv je možné brať správnosť vzťažných údajov generovaných programom MS Excel 2007, ďalej voľba štatistického súboru na spracovania. Ako som už spomínal výstupný log zo simulácie bol veľmi rozsiahly a pre spravovanie som vybral len časť dát (technická manipulácia s viac ako štvrť miliónom údajov v programe MS Excel 2007 nie je možná). Je teda viac ako pravdepodobné, že so sofistikovanejšími CAE programami by mohli byť výsledky presnejšie. Netransparentnosť výsledkov mohla rovnako vzniknúť už pri tvorbe vstupných skriptov, nakoľko práve tu sa charakterizuje tvorba zhlukov
Záver
Ako som už spomínal v úvode tejto práce, mojim cieľom je overiť korektnosť generátorov prevádzkových tokov. To sa mi aj podarilo vďaka experimentom pri tvorbe simulácií. Z výsledkov simulácií som získal potrebné dáta do následného spracovania. Zo štatistického spracovania som zistil, že pri 5% hladine významnosti môžem zamietnuť nulovú hypotézu pri 5 simuláciách z 9. Pri zvyšných štyroch nie je možné nulovú hypotézu zamietnuť t.j. je štatisticky nevýznamná. Za 100% korektné možno považovať pracovanie generátora pri tvorbe zhlukov s exponenciálnym rozdelením. Naopak za najmenej korektné je možné považovať správanie sa generátora s rovnomerným tvorením zhlukov. Všeobecne je však možné simulácie a experimenty považovať za úspešné. Implementovanie získaných výsledkov do praxe je možné realizovať pomocou internetového fóra na stránkach National Chiao Tung University v Taiwane, kde profesor S. Wang zbiera informácie od študentov z celého sveta. Implementovaním výsledkov je možné vylepšiť vlastnosti simulačného prostredia NCTUns a pomôcť tak sieťovým inžinierom získavať korektnejšie informácie pri simuláciách OBS sietí, nakoľko možná budúcnosť, kadiaľ smerovať WDM optické siete, je práve OBS technológia.
Použitá literatúra
- BATTESTILLI, Tzevetelina, PERROS, Harry. An Introduction to Optical Burst Switching. IEEE Optical Communications. August 2003, no. ?, s. 10-15.
- CISCO Networking Academy : CCNA [online]. c1992 , 26.11.2009 [cit. 2009-12-03]. Dostupný z WWW: <http://www.cisco.com/web/learning/netacad/index.html>.
- NCTUns 6.0 Network Simulator and Emulator [online]. c1999 , 11.11.2009 [cit. 2009-12-03]. Dostupný z WWW: <http://nsl.csie.nctu.edu.tw/nctuns.html>.
- SHIE - YUAN, Wang; CHIN - LIANG, Chou; CHIN - CHE, Lin. The GUI User Manual for the NCTUnc 6.0 Netowork Simulator and Emulator. In [online]. [s.l.] : Network and System Laboratory, Department of Computer Science, September 2009 [cit. 2010-06-07].
- BAHLEDA, Miroslav. Just-in-time Optical Burst Switching. Science, Education and Society : 11th International Scientific Conference. 2003, roč. 11, s. 1-19. Dostupný z WWW: <http://www.bahleda.sk/dokumenty/pub/jit-obs.ppt>.
- HRUBÝ, Martin, et al. Simulátor komunikácie v počítačovej sieti. [s.l.], 2009. 59 s. Slovenská technická univerzita, Fakulta informatiky a informačných technológií. Vedúci tímovej práce Ing. I. Grellneth, PhD.
- RIMARČÍK, Marián. Http://rimarcik.com/ [online]. 2000 [cit. 2010-07-06]. Štatistická analýza. Dostupné z WWW: http://rimarcik.com/navigator/chi.html
- Http://new.euromise.org/ [online]. 5.1.1999 [cit. 2010-07-06]. Analýza kategoriálních dat. Dostupné z WWW: <http://new.euromise.org/czech/tajne/ucebnice/html/html/node12.html>.
- ARACIL, Javier, Prof. et al. The e-Photon/ONe research agenda in Optical Burst Switching : Bustification algorithms. Dostupný z WWW: < http://eurongi.enst.fr/archive/168/aracil.ppt>.
Slovník
- Anycast
- Adresovanie vybratým zariadeniam v sieti
- Broadcast
- Adresovanie všetkým zariadeniam v sieti
- Burst
- Zhluk prenášaných dát s variabilnou veľkosťou
- Fairness
- Pravidlá zdieľania prenosových kapacít
- Next hop
- Proces preposielania paketov pri smerovaní
- OBS
- Optická sieť s prepojovaním zhlukov
- Offset Time
- Oneskorenie
- OS
- Operačný systém
- Paket
- Balíček prenášaných dát
- Poissonov model
- Forma regresnej analýzy využívanej v štatistike
- QoS
- Kvalita služieb
- Router
- Smerovač, zariadenie zabezpečujúce komunikáciu medzi sieťami
- Self-similarity
- Seba podobnosť
- Throughput
- Hranica priepustnosti siete
- Token
- Príznak charakterizujúci spôsob spracovania dát
- Topológia
- Fyzická a logická architektúra počítačovej siete
- Vlnová dĺžka
- Vzdialenosť medzi opakujúcimi sa periódami vlnenia
Skratky a akronymy
- AON
- All Optical Network
- BER
- Bit Error Rate
- CAE
- Computer Aided Engineering
- CoS
- Class of Service
- GMPLS
- Generalized Multiprotocol Label Switching
- GUI
- Graphic User Interface
- JET
- Just Enough Time
- MPLS
- Multiprotocol Label Switching
- OBS
- Optical Burst Switching
- OBSN
- Optical Burst Switched Network
- OEO
- Optical-Electrical-Optical
- OPSN
- Optical Packet Switched Network
- QoS
- Quality of Service
- RWA
- Routin and Wavelenght Allocations
- SOA
- Service-oriented architecture
- WDM
- Wavelenght Division Multiplexing
- WR
- Wavelenght Routing
- WRN
- Wavelenght Routed Network