Vybrané metódy a nástroje analýzy spracovania dát v manažérstve kvality

Obsah práce

1.	Manažérstvo kvality
2.	Vybrané metódy a nástroje analýzy spracovania dát v manažérstve kvality
3.	Metódy plánovania kvality

Dôležitú skupinou metód a nástrojov manažérstva kvality predstavuje sedem základných nástrojov manažérstva kvality, ktoré boli rozvinuté v Japonsku K. Ishikawom a W. E. Demingom. Sedem základných nástrojov sa používa pri riešení problémov operatívneho riadenia kvality a pri zlepšovaní kvality.

K siedmim základným nástrojom manažérstva kvality sa radí:

• vývojový diagram
• diagram príčin a následku
• formulár pre zber údajov
• Paretov diagram
• histogram
• bodový diagram
• regulačný diagram

Poradie, v ktorom sa sedem základných nástrojov uvádza býva rôzne. Uvedené poradie sa snaží kopírovať najčastejšiu postupnosť ich používania pri riešení problémov s kvalitou. Vývojový diagram je na prvom mieste preto, že by mal slúžiť k dokonalému poznaniu analyzovaného procesu, identifikovať jeho jednotlivé kroky, odpovedajúce vstupy a výstupy a vzájomnú naviazanosť jednotlivých činností.

Dokonalejšie poznanie procesu pomocou vývojového diagramu sa premieta do zvýšenej efektívnosti aplikácie diagramu príčin a následku, ktorý je základným nástrojom analýzy všetkých možných príčin riešeného problému. Identifikácia všetkých možných príčin je dôležitým východiskom pre plánovanie zberu údajov potrebných pre sledovanie riešeného problému a pre vyhodnotenie miery pôsobenia jednotlivých príčin. Informácie zhromaždené v diagrame príčin a následku sú veľmi dôležitým podkladom pre prípravu formulára resp. formulárov pre zber údajov. Spracovanie formuláru pre zber údajov, ktoré môžu mať aj elektronickú podobu, je základným východiskom pre zmysluplné a systematické zhromažďovanie jednotlivých dát.

Vývojový diagram

Vývojový diagram slúži k názornému grafickému zobrazeniu postupnosti a vzájomnej náväznosti všetkých krokov určitého procesu. Jeho spracovanie je dôležitým východiskom zlepšovania procesov a teda aj kvality. Dá sa využiť k popisu akéhokoľvek procesu, pričom sa môže jednať o existujúci, alebo ešte len navrhovaný proces. Vývojový diagram je vhodným nástrojom pre analýzu procesu, jeho jednotlivých krokov a rozhodovacích uzlov, pre identifikáciu oblastí, kde môžu vznikať problémy, pre optimalizáciu rozmiestenia kontrolných miest a pre identifikáciu nadbytočných činností. Predstavuje názorné zobrazenie procesu, ktoré prispieva k jeho lepšiemu a a rýchlejšiemu pochopeniu. Pracovníkom zapojených do procesu presne vymedzí ich postavenie a ich vnútorných zákazníkov. Tieto nesporné výhody vývojového diagramu neznižuje ani skutočnosť, že v prípade zložitých procesov môže jeho aplikácia viesť niekedy až k prílišnému zjednodušeniu, čo súvisí napríklad s obtiažnym zachytením výnimiek alebo súbežných činností [2].

Pravidlá zostavenia vývojového diagramu

Pri tvorbe vývojového diagramu je potrebné dodržiavať tieto zásady:

• Zostavovať vývojový diagram v tíme.
• Vhodne zvoliť otázky. Základné otázky typu: „Čo sa stalo najskôr?“, „Čo má nasledovať?“
• Udržať popis procesu jednoduchý, stručný a prehľadný.
• Zaistiť istú jazykovú formu popisu činností (napr. všetky činnosti vyjadriť infinitívom) a udržať úroveň ich podrobností v rámci popisovaného procesu.
• Správne identifikovať rozhodovanie.
• Snažiť sa o umiestenie jedného vývojového diagramu na jednu stránku.
• Využívať jednotnú symboliku (najčastejšie používané symboly a ich význam sú uvedené v tabuľke 1).
• Používať jeden blok začiatku a jeden blok konca.
• Zobraziť orientáciu v rámci procesu.

Postup zostavenia vývojového diagramu

Pri zostavovaní vývojového diagramu treba postupovať takto:

• Identifikovať proces, jeho rozhranie s inými procesmi a činnosťami.
• Zostaviť tím (všetci, ktorí sa zúčastnia realizácie procesu).
• Schváliť symboly, ktoré budú vo vývojovom diagrame použité, vrátane ich významu.
• Zakresliť symbol pre začiatok procesu.
• Identifikovať prvú činnosť (otázka „Čo sa stalo najskôr?“) a zakresliť symbol a popis prvej činnosti.
• Identifikovať ďalšie činnosti a miesta, kde prebieha rozhodovanie, vrátane záznamu opatrenia pre všetky možnosti rozhodnutia (otázky: „Čo sa stane ďalej?“, „Čo sa stane keď...?“), zakresliť ich do diagramu a spojiť šípkami.
• Po poslednej činnosti zakresliť symbol pre koniec procesu.
• Jednoznačne identifikovať vývojový diagram (uviesť názov procesu, autorov vývojového diagramu, meno používateľa, číslo varianty vývojového diagramu, dátum poslednej revízie...).

Diagram príčin a následku (Ishikawov diagram)

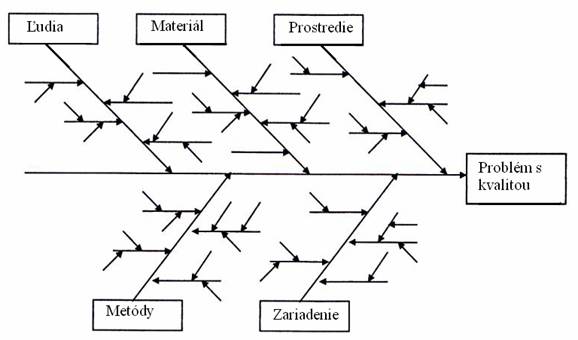
Diagram príčin a následku je dôležitým grafickým nástrojom pre analýzu všetkých príčin určitého následku (problému s kvalitou). Jeho použitie predstavuje systémový prístup k riešeniu problému, ktorý pomáha všetky myšlienky a námety. Diagram príčin a následku by sa mal stať prvým krokom riešenia všetkých problémov, ktoré môžu byť vyvolané viacerými príčinami. Spracovanie diagramu príčin a následku je jednoduché a ľahko pochopiteľné , čo umožňuje zapojenie širšieho okruhu pracovníkov do riešenia problému. Aplikácia diagramu príčin a následku často prináša námety, ktoré vedú k novým, nekonvenčným riešeniam. Na obrázku 2.1 je znázornená štruktúra diagramu príčin a následku

Obr 2.1 Štruktúra diagramu príčin a následku

Postup zostrojenia Ishikawovho diagramu

Postup zostrojenia Ishikawovho diagramu môžeme rozdeliť na 2 časti, a to prípravu brainstormingu a realizáciu brainstormingu. V rámci prípravy je potrebné previesť výber vhodnej miestnosti a doby konania, výber vhodného kolektívu (cca 5- 8 osôb), prichystať veľký hárok papiera alebo tabuľu pre zápis nápadov (príčin efektu), nakresliť základnú kostru diagramu. V rámci realizácie brainstormingu je potrebné zvolať kolektív, vyvesiť základnú kostru diagramu na všetkými viditeľné miesto, zvoliť moderátora, definovať problém alebo očakávaný prínos, tj. efekt (efekt je nutné definovať tak, aby nebol pojatý ani príliš úzko, ani príliš široko), ďalej definovať všeobecné hlavné skupiny príčin [najčastejšie: ľudia, materiál, prostriedky, metódy, stroje (zariadenia)]. Potom sa uskutoční samotný brainstorming a to nasledovne:

• moderátor postupne vyzýva každého člena tímu, aby sformuloval subpríčinu či elementárnu príčinu analyzovaného efektu;
• tento proces sa prevádza v niekoľkých kolách tak dlho, až členovia tímu vyčerpajú všetky svoje nápady;
• všetky nápady sa zaznamenávajú do Ishikawovho diagramu.

Vyhodnotenie Ishikawovho diagramu

Pri vyhodnotení môžeme postupovať v týchto krokoch:

• Stanovenie najpravdepodobnejších príčin analyzovaného efektu.
• Určenie najdôležitejších príčin.
• Analýza najdôležitejších príčin.

Túto úlohu je možné vyriešiť pomocou tzv. metódy bodového hodnotenia, kedy každý člen riešiteľského tímu dostane určitý počet bodov (napr. 6), v niekoľkých kolách (najčastejšie v troch) postupne prideľuje body podľa vlastnej úvahy najpravdepodobnejším príčinám tak, aby bol vyjadrený rozdiel v ich príspevku k analyzovanému následku (napr. v prvom kole sa prihadzujú 3 body, v druhom kole 2 a v treťom 1 bod). Takto kvantifikované príčiny sa ďalej spracujú napr. pomocou Paretovej analýzy, ktorej výsledkom je určenie najdôležitejších príčin. Ďalej je potrebné navrhnúť a skúšobne zaviesť opatrenia na odstránenie najdôležitejších príčin, previesť zber a záznam dát k zisteniu vplyvu prijateľných opatrení, dáta vyhodnotiť pomocou opakovanej Paretovej analýzy a výsledky porovnať s výsledkami analýzy pred prijatím nápravného opatrenia. V prípade, že došlo k zlepšeniu, je potom možné zaviesť prijaté opatrenia procesu štandardne [3].

Formulár pre zber údajov

Formuláre pre zber údajov (kontrolné záznamníky) sú určené k systematickému zhromažďovaniu údajov relevantných pre riadenie a zlepšovanie kvality. Zozbierané údaje sú základným východiskom pre hodnotenie existujúceho stavu procesov a pre určenie smerov ďalšieho zlepšovania. Formuláre pre zber údajov nemusia mať vždy papierovú podobu. V súčasnom rozvoji informačných systémov môžu byť spracované v elektronickej podobe a zdieľané pracovníkmi z rôznych pracovísk s presne vymedzenými prístupovými právami [2]. Pri plánovaní zberu dát je potrebné vychádzať z toho, aké informácie je potrebné získať, pričom vypovedacia schopnosť informácie nezávisí len na počte získaných údajov, ale najmä na vhodnej voľbe sledovaných parametrov. Vzhľadom k tomu, že informácie získané na základe zozbieraných údajov predstavujú dôležitý prostriedok poznania a východzí predpoklad kvalifikovaných rozhodnutí, je potrebné sa vyvarovať informáciám, ktoré sú:

• neúplné, tj. informácie získané na základe neúplných údajov;
• oneskorené, tj. informácie, ktoré vzhľadom k oneskorenému spracovaniu údajov nie sú k dispozícii načas;
• skreslené, t.j. informácie získané na základe nesprávne zistených, nesprávne identifikovaných alebo nesprávne spracovaných údajov.

Formuláre pre zber údajov majú byť dobre zrozumiteľné a dostatočne prehľadné a ich usporiadanie musí zabezpečiť dostatok miesta pre čitateľný záznam údajov. Formuláre musia taktiež umožňovať záznam údajov o všetkých dôležitých podmienkach, za ktorých boli zozbierané dáta získané. Znalosť všetkých týchto identifikačných údajov má veľký význam pre stratifikáciu dát, teda pre triedenie dát podľa určitých hľadísk. Možnosť stratifikácie dát je veľmi dôležitá pre ďalšie hodnotenie údajov. Vhodnými hľadiskami pre stratifikáciu údajov sú napríklad:

• druh zistenej nezhody;
• vymedzenie oblasti, kde bola nezhoda zistená;
• príčina vzniku nezhody (rovnaká nezhoda môže mať niekoľko príčin);
• druh použitého materiálu
• časový úsek výroby;
• výrobná linka;
• obsluha;
• technologické parametre výroby;
• parametre prostredia
• použité meracie prostriedky atd.

Pred spracovaním formulára pre zber údajov je potrebné stanoviť aké informácie majú zozbierané údaje poskytnúť (na aké otázky majú odpovedať). Na základe tohto ujasnenia sa stanový aké údaje je nevyhnutné k dosiahnutiu daného účelu zhromaždiť. Po identifikácii potrebných údajov a upresnení spôsobu, ako budú údaje získavané a analyzované, sa spracuje návrh formulára pre zber údajov. Mala by v ňom byť prehľadne a v logickom slede usporiadaná miesta pre záznam údajov a mal by obsahovať oblasť pre záznam základných identifikačných znakov a všetkých podmienkach, za ktorých boli údaje zhromaždené. Uvedený postup spracovania formulára pre zber údajov predchádza vzniku v praxi častých problémov, kedy sa až dodatočne zisťuje, že zhromaždené údaje sú neúplné a neumožňujú vyhodnotiť vplyvy niektorých faktorov [2].

Paretov diagram

Paretov diagram je dôležitým nástrojom manažérskeho rozhodovania, pretože umožňuje stanoviť priority pri riešení problémov s kvalitou tak , aby pri účelnom využití zdrojov bol dosiahnutý maximálny efekt. Je taktiež vhodný pri názornej prezentácii problému. Taliansky sociológ a ekonóm Vilfredo Pareto v 19. storočí zistil, že 80 % bohatstva vlastní 20 % obyvateľstva. Americký odborník na kvalitu J. M. Juran označil zovšeobecnenie tohto rozdelenia ako Paretov princíp a na jeho základe sformuloval záver, že 80 – 95 % problémov s kvalitou je spôsobených malým počtom príčin (5 – 20 %). Na príčiny tvoriace túto menšinu je v ďalšej analýze procesu treba prednostne zamerať pozornosť, analyzovať ich do hĺbky a odstrániť či minimalizovať ich pôsobenie [3]. Prostriedkom uplatnenia Paretovho princípu a základným nástrojom Paretovej analýzy je Paretov diagram. V oblasti riadenie kvality je Paretov diagram jedným z najefektívnejších bežne dostupných a ľahko aplikovateľných rozhodovacích nástrojov. Je to stĺpcový graf zobrazujúci Paretove rozdelenie. Stĺpce sú zoradené od najvyššieho k najnižšiemu. Paretova analýza je technika využívajúca Paretovho princípu v rámci procesu riešenia problému ku stanoveniu priorít. Realizuje sa na základe konštrukcie Paretovho diagramu a následného uplatnenia Paretovho princípu či ďalších kritérií pre výber životne dôležitej menšiny. Cieľom Paretov analýzy je teda oddeliť podstatné faktory ( napr. príčiny určitého problému s úrovňou kvality) od menej podstatných a ukázať, kam prednostne zamerať úsilie pri zlepšovaní procesov. Využitie Paretovej analýzy v oblasti manažérstva kvality je mnohostranné. Môže ísť o nasledujúce oblasti [3]:

• analýza počtu nezhodných výrobkov a ich druhov;
• analýza strát s nimi spojených;
• analýza časových a finančných strát spojených s vysporiadaním nezhodných výrobkov;
• analýza reklamácii z hľadiska finančných strát či dôvodov reklamácii;
• analýza príčin výroby nezhodných výrobkov;
• analýza príčin prestojov strojov;
• analýza porúch a havárii zariadení;
• analýza opotrebovania náradia;
• porovnanie stavu pred realizáciou a po realizácii opatrení na zlepšenie.

Paretovu analýzu možno úspešne využiť ako pri vyhľadávaní a pri definovaní najpodstatnejších problémov, ktoré sú napr. najpočetnejšie alebo najnákladnejšie, tak pri stanovení „životne dôležitej menšiny“ príčin, ktoré spôsobujú vopred definovaný, už odhalený problém.

Postup pri Paretovej analýze

Pri Paretovej analýze sa realizujú tieto kroky:

• voľba faktorov;
• voľba hľadiska analýzy;
• zber a záznam dát;
• zostrojenie Paretovho diagramu;
• voľba kritéria pre stanovenie životne dôležitej menšiny faktorov a stanovenie životne dôležitej menšiny faktorov;
• analýza faktorov stanovených ako životne dôležitá menšina.

Voľba faktorov je daná problémom, ktorý je treba vyriešiť. Môže ísť napr. o vysoký výskyt závad (faktory budú jednotlivé druhy závad), vysoký výskyt reklamácii (faktory budú rôzne produkty), časté poruchy strojov (faktory budú typy strojov) a pod. Každý problém možno hodnotiť z troch základných hľadísk:

• z hľadiska početnosti jednotlivých faktorov (napr. sa analyzuje počet reklamácii v členení podľa jednotlivých odberateľov;
• z hľadiska nákladového (reklamácie sú vyjadrené v stratách s nimi spojených);
• z hľadiska významnosti sledovaných faktorov (napr. z pohľadu bezpečnosti či funkčnosti výrobkov).

Voľba hľadiska a sledovaného ukazovateľa závisí na cieľoch a prioritách riešenia problémov. Analýza môže byť prevádzaná iba podľa jedného hľadiska, ale môže byť tiež prevádzaná tzv. viacnásobná Paretova analýza, kedy sa problém analyzuje z niekoľkých hľadísk, a faktory, na ktoré je potrebné sa pri riešení problémov prednostne zamerať, sú tie, ktoré vytvárajú únik všetkých získaných životne dôležitých menšín. Pri zostrojení Paretovho diagramu je treba previesť nasledujúce činnosti:

• zotriedenie faktorov zostupne podľa hodnôt zvoleného ukazovateľa;
• výpočet absolútnej kumulatívnej početnosti a kumulatívnej početnosti v %;
• zostrojenie Paretovho diagramu, t.j.
• vyznačenie jednotlivých faktorov na osi x,
• zostrojenie ľavej osi y a pravej osi y,
• zakreslenie stĺpcov pre jednotlivé faktory,
• zostrojenie Lorenzovej krivky (spojnice bodov, ktoré sú pravými hornými rohmi jednotlivých stĺpcov).

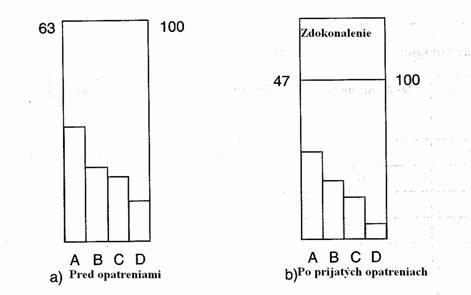
Základným kritériom pre stanovenie životne dôležitej menšiny faktorov je kritérium 80/20 (Paretov princíp). Kritérium uplatníme tak, že na pravej osi y odčítame 80% a premietneme ich cez Lorenzovu krivku na os x. Faktory, ktoré ležia vľavo od kolmice spustenej z Lorenzovej krivky na os x, tvoria hľadanú životne dôležitú menšinu faktorov. Tiež sám priebeh Lorenzovej krivky môže napovedať, kadiaľ vedie hranica medzi životne dôležitou menšinou faktorov a užitočnou väčšinou – hranice vedú bodom, ktorý predstavuje výrazný zlom v priebehu tejto krivky. Ak je Paretove rozdelenie plošného tvaru, nevedie uplatnenie kritéria 80/20 k vymedzeniu menšiny. V tomto prípade bude vhodnejšie napr. kritérium 70/30 alebo 50/50. Ďalšou možnosťou je použitie tzv. kritéria priemernej hodnoty zvoleného ukazovateľa. Hranicu „životne dôležitej menšiny“ stanovíme v tomto prípade tak, že postupne porovnávame hodnotu zvoleného ukazovateľa u jednotlivých faktorov s priemernou hodnotou tohto ukazovateľa. Faktor, kde je hodnota daného ukazovateľa menšia než priemerná hodnota, už nepatrí do „životne dôležitej menšiny“ a nie je zahrnutý do hlbšej analýzy rovnako ako všetky po ňom nasledujúce faktory. Posledným krokom Paretovej analýzy je vlastná analýza faktorov vymedzených ako životne dôležitá menšina s cieľom prijať nápravné opatrenia vedúce k obmedzeniu vplyvu týchto faktorov a k zlepšeniu procesu. Paretov diagram potom možno opakovane použiť k vyhodnoteniu účinnosti prijímaných opatrení. Ak zobrazíme pomocou Paretovho diagramu stav pred prijatím opatrení a stav po jeho implementácii, mal by byť z porovnania dvoch diagramov vnímateľný účinok opatrení, ako je naznačené na obrázku 2.2.

Obr 2.2 Aplikácia Paretovho diagramu k vyhodnoteniu účinnosti prijatého opatrenia

Veľmi efektívna je aplikácia Paretovho diagramu v kombinácii s analýzou pomocou diagramu príčin a následku. Majme napr. problém s vysokým výskytom závad u určitého produktu. Pre tento prípad je vhodná nasledujúca sekvencia nástrojov:

• Paretova analýza početnosti závad podľa jednotlivých druhov závad;
• analýza príčin „životne dôležitých príčin“ pre „životne dôležité chyby“ pomocou Paretovho diagramu [3].

Histogram

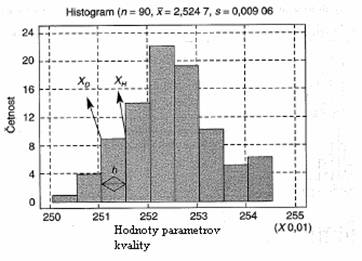
Histogram (obrázok 2.3) je stĺpcový diagram znázorňujúci rozdelenie početnosti hodnôt vo vhodne zvolených intervaloch (triedach) a je považovaný za základný grafický nástroj hodnotenia zhromaždených údajov. Je potrebné upozorniť, že zostrojenie histogramu má zmysel až od určitého počtu hodnotených údajov (minimálne cca 30 hodnôt). U menej rozsiahlych súborov možno ku grafickému znázorneniu rozdelenia sledovaného znaku využiť napríklad krabicový diagram, v ktorom sa zobrazujú úrovne kvantilov, minimálna a maximálna hodnota súboru a prípadné odľahlé hodnoty [2].

Obr 1.1 Ukážka histogramu

Podkladom pre konštrukciu histogramu je tabuľka intervalového rozdelenia početnosti hodnôt. K odhadu vhodného počtu intervalov možno v literatúre nájsť radu empirických vzťahov, podľa ktorých sa počet intervalov počíta ako funkcia počtu hodnôt v spracovávanom súbore. V prípade, že sa vytvorí príliš málo intervalov, tak získaný histogram neposkytne očakávanú informáciu o charaktere rozdelenia hodnôt, ak sa naopak vytvorí príliš veľa intervalov, bude histogram príliš členitý a jeho využiteľnosť pre ďalšiu analýzu bude opäť veľmi malá [2]. Pri stanovení vhodnej šírky intervalu (z hľadiska analýzy tvaru histogramu je žiaduce, aby bola konštantná) sa vychádza z variačného rozpätia nameraných hodnôt a zvoleného počtu intervalov. Na základe stanovenej šírky intervalu a vhodne stanovenej hranice prvého intervalu sa potom stanovuje hranica jednotlivých intervalov. Dolná hranica prvého intervalu by mala byť volená tak, aby v prvom intervale bola obsiahnutá minimálna hodnota a bolo zaistené jednoznačné priraďovanie hodnôt do všetkých intervalov. Pre splnenie druhej požiadavky je vhodné, aby hranice intervalov boli stanovené o radu presnejšie ako spracovávané hodnoty, teda aby nemohol nastať prípad, že niektorá z hodnôt sa rovná hranici intervalu. Vhodnou hranicou intervalu je napríklad aritmetický priemer dvoch po sebe idúcich na merateľných hodnôt [2].

Postup zostrojenia histogramu

Zostrojenie histogramu možno zhrnúť do nasledujúcich krokov:

• Výpočet rozpätia súboru R.
• Stanovenie počtu a šírky intervalov.
• Zostavenie tabuľky početnosti.
• Stanovenie hraníc intervalov.
• Stanovenie stredov intervalov (triednych znakov).
• Priradenie nameraných hodnôt do jednotlivých intervalov v tabuľke početností pomocou čiarkovej metódy.
• Zostrojenie vlastného diagramu.

Interpretácia histogramu

• Analýza tvaru histogramu umožňuje posúdiť
• typ rozdelenia (symetrické, asymetrické)
• pôsobenie identifikovateľných príčin variability (najčastejšie sa vyskytujúce tvary histogramov vrátane možných identifikovateľných príčin sú uvedené v tabuľke 2). Ak je analýzou preukázané, že sledovaný znak kvality či parameter procesu má normálne rozdelenie, potom by histogram mal mať zvonovitý tvar, ktorý signalizuje, že na proces pôsobia iba náhodné vplyvy, a že je tak v štatisticky stabilnom stave. Každá odchýlka od tohto tvaru potom signalizuje pravdepodobne pôsobenie identifikovateľných vplyvov.
• Z histogramu možno previesť odhad štatistických ukazovateľov polohy a menlivosti [3].

Bodový diagram

Bodový diagram je grafickou metódou pre štúdium vzťahov medzi dvomi premennými. Pomocou bodového diagramu možno posudzovať napríklad vzájomnú súvislosť medzi dvomi znakmi kvality výrobku, súvislosti medzi určitým znakom kvality výrobku a jednotlivými parametrami procesu, posudzovať ako ďaleko údaje meradla zodpovedajú referenčným hodnotám. a pod [2]. Rozmiestenie bodov v bodovom diagrame, ktoré zodpovedajú jednotlivým dvojiciam hodnôt príslušných premenných, charakterizuje smer, tvar a mieru tesnosti závislosti medzi sledovanými premennými. Vo väčšine prípadov sa v praxi stretávame s voľnými závislosťami, ktoré sú charakteristické určitým rozptylom bodov. Príčinou tohto rozptylu je najčastejšie pôsobenie ďalších vplyvov, ako je napríklad variabilita parametrov procesu, vonkajších podmienok, vlastností použitých materiálov a pod. Na rozptyle hodnôt sa taktiež podieľa nepresnosť stanovenia hodnôt zodpovedajúcich premenných, ktoré ovplyvňuje rada parametrov, napríklad nepresnosť metódy stanovenia, nepresnosť meracieho zariadenia, nepresnosť obsluhy a pod [2].

Postup zostrojenia bodového diagramu

Pri konštrukcii bodového diagramu sa postupuje nasledovne:

• Zvolíme nezávislú premennú X a závislú premennú Y (napr. menej nákladnú a menej presnú metódu a metódu presnejšiu a nákladnejšiu).
• Prevedieme meranie minimálne 30 dvojíc hodnôt závislej a nezávislej premennej (Xi, Yi) či ešte lepšie 50 – 100 dvojíc a zaznamenáme ich do tabuľky [dvojice nameraných hodnôt (Xi, Yi) predstavujú dvojrozmerný náhodný výber rozsahu n ≥ 30 ].
• Z nameraných hodnôt zostavíme bodový diagram tak, že dvojice hodnôt (Xi, Yi) znázorníme v pravouhlej súradnicovej sústave (X, Y). Každá dvojica (Xi, Yi) je zobrazená bodom o súradniciach [Xi, Yi].
• Prevedieme analýzu bodového diagramu.

Interpretácia bodového diagramu

Vlastná analýza bodového diagramu môže poskytnúť cenné prvotné informácie a študovanom znaku kvality, resp. o procese, ktorého je tento znak kvality výsledkom. Základné typy stochastických závislostí sú na obrázku 2.4. Bodové diagramy na obrázku a) a c) ukazujú prípad priamej lineárnej stochastickej závislosti. Na obrázku a) ide o silnú koreláciu, pretože body sú veľmi málo rozptýlené. Obrázky b) a d) ukazujú nepriamu lineárnu závislosť, ktorá je na obrázku b) silnejšia ako na obrázku d). Z tvaru zoskupenia bodov na obrázku f) môžeme usudzovať na nelineárnu stochastickú závislosť. Na obrázku e) sú body rozptýlené po celej ploche diagramu. Z toho možno usudzovať, že premenné X a Y nie sú korelované a neexistuje medzi nimi žiadna stochastická závislosť. Ak chceme prvotnú informáciu z bodového diagramu spresniť, prevedieme kvantifikáciu tesnosti stochastickej závislosti. Postup merania stochastickej závislosti sa nazýva korelačná analýza [3].

Regulačný diagram

Regulačný diagram graficky zobrazuje dynamiku procesu, t.j. zmenu ukazovateľa kvality na čase (premenlivosť parametra na čase). V diagrame je označený rozsah nevyhnutného rozptylu, ktorý leží v intervale hornej a dolnej regulačnej medze. Pre odhad regulačných medzí sa používa 3- násobok smerodajnej odchýlky. Regulačné diagramy sa používajú pri analýze a regulácií technologických procesov a na ich zlepšovanie. Regulačný diagram (Control diagram) predstavuje graf, zobrazujúci dynamické zmeny vybraných ukazovateľov kvality v čase, v závislosti od systematických vplyvov. Regulačný diagram je používaný na stanovenie procesu, ktorý bude produkovať výrobok alebo službu s pevnými merateľnými vlastnosťami. Je základným grafickým nástrojom, umožňujúcim odlíšiť variabilitu procesu, vyvolanú zvláštnymi príčinami od variability vyvolanej náhodnými príčinami. Využíva sa pre analýzu a tiež pre kontrolu a riadenie procesov [7]. Regulačný diagram sa využíva k analýze procesu a je tiež základným nástrojom štatistickej regulácie procesu (SPC - Statistical Process Control). Štatistická regulácia procesu predstavuje systém spätnej väzby, ktorého základným cieľom je dosiahnutie a udržanie stavu, v ktorom proces prebieha na stabilnej úrovni a trvale poskytuje výrobky, ktoré vyhovujú požadovaným kritériám kvality. Štatistická regulácia je založená na stratégii prevencie, teda na stratégii, ktorá predchádza vzniku nezhodných výrobkov, pretože svoju pozornosť sústreďuje tam, kde kvalita vzniká a možno ju ovplyvniť. Stratégia prevencie výrazne znižuje náklady na triediacu kontrolu, na materiál, čas a mzdy potrebné na výrobu nezhodných výrobkov a predstavuje zásadný posun oproti predtým presadzovanej stratégii detekcie, ktorá sa najmä sústredila na následnú kontrolu už vyrobených výrobkov [2].

Postup tvorby regulačného diagramu

• Urobiť vzorku náhodných dát z procesu, zmerať charakteristiky kvality a vypočítať

premenné alebo zmerať atribúty

• Ak na znázornenom diagrame dáta prekračujú medze, zamerať sa na ich príčiny.
• Potom eliminovať alebo odstrániť príčiny a zostrojiť regulačný diagram znovu

Nevyhnutnosťou pri zostrojovaní regulačných diagramov je, na rozdiel od konštrukcie histogramov, zachovanie poradia získavaných údajov v čase. Základom regulačného diagramu – RD je zobrazenie dát v dvojrozmernom súradnicovom systéme. Os x-ová je osou časovou, os y-ová je osou hodnôt/dát. Dáta sa navzájom spájajú do poly-gónu - priebehového diagramu (Runchart) - časového radu. Kľúčovým atribútom pri regulačných diagramoch je čas a racionálne zoskupenie údajov v ňom [8]. V diagrame je znázornená trojica kritérií: • stredná priamka/čiara - CL (Central Line), • horná regulačná medza/hranica - UCL (Upper Control Limit), • dolná regulačná medza/hranica - LCL (Lower Control Limit), • (ak LCL je záporné číslo, uvažuje sa s LCL=0), Aj keď majú regulačné diagramy rovnakú, jednotnú formu, líšia sa podľa typu regulovaných veličín, podľa spôsobu výpočtu regulačných medzí, ako aj podľa počtu a rozsahu spracovávaných výberov. Existujú dva základné typy regulačných diagramov, konštruované pre dáta získavané, meraním (premenných veličín) a porovnávaním (vlastností premenných). Pri štatistickej regulácii porovnávaním sa zisťuje zhoda/nezhoda s normou/etalónom. Hodnotí sa súhrn funkčných a technických požiadaviek. Pri tomto postupe sa sleduje celkový počet nezhodných produktov, podiel nezhodných produktov, alebo počet chýb na jeden výrobok pri opakovaných výberoch. Pre zabezpečenie primeranej vypovedacej schopnosti je potrebné, aby jednotlivé výbery mali rozsah 20 a viac hodnôt, a aby celková veľkosť porovnávaného súboru bola bola 200 a viac hodnôt [8].