Metódy analýzy v oblasti logistického riadenia nákupu
Obsah
Metódy analýzy v oblasti logistického riadenia nákupu
V tejto kapitole si poukážeme na rôzne metódy analýzy v oblasti logistického riadenia nákupu. Logistika je veľmi široká vedná disciplína, ktorá na stanovenie úzkych miest v toku materiálov využíva celú radu metód analýzy. Hlavné členenie týchto metód je nasledovné:
- Exaktné metódy.
- Heuristické metódy [4].
Jednotlivé metódy si rozoberieme podrobnejšie v nasledujúcich podkapitolách, pričom sa zameriame hlavne na metódy operačnej analýzy, a to teórie zásob.
Exaktné metódy
Používajú sa najmä pre optimalizačné úlohy rozhodovacích procesov, kde využívajú poznatky nadobudnuté z rôznych vedných disciplín, najmä z matematických disciplín. Patria sem:
- Štatistické metódy- zaoberajú sa získavaním (meraním), popisom a spracovávaním údajov s cieľom nájsť zákonitosti náhodných hromadných javov vyskytujúcich sa v procese zásobovania, mieru závislosti dvoch alebo viacerých náhodných hromadných javov a na základe výberového súboru hodnôt získať odhad rozloženia pravdepodobnosti.
- Metódy analýzy logistických procesov- sem patria napr.:
- Systémová analýza- jej hlavnou úlohou je objasnenie celkových logistických proces v spojení s nákupom [4].
- Analýza ABC- najčastejšie používaná analýza, ktorá slúži napr. na výber.
- Analýza XYZ- slúži na zistenie časového priebehu toku sortimentu cez logistický reťazec [7].
- Hodnotová analýza- princíp tejto analýzy spočíva v hodnotení hospodárnosti pri toku sortimentu cez logistický reťazec.
- Analýza nákladov- slúži na určenie nákladov v pohybových úsekoch logistiky [4].
- Metódy operačnej analýzy- pomocou matematických disciplín modelujú stavy rozhodovacích a technologických procesov. V logistike obstarávania zásob sa uplatňujú predovšetkým:
- teória zásob- táto metóda analýzy je podrobne opísaná v podkapitole 2.4,
- teória obnovy,
- teórie frontu,
- lineárne programovanie.
- Metódy teórie grafov- sú to metódy optimalizačné, ktoré pri riešení rôznych nákupných logistických problémov využívajú grafické spracovania. Sú oveľa prehľadnejšie a poskytujú viac informácií ako ostatné metódy.
- Prognostické metódy- tvorením prognóz sa získava prehľad o budúcom vývoji alebo o budúcich udalostiach. Táto metóda sa používa hlavne pri obstarávaní dlhodobých zásob [4].
- Simulačné metódy- používajú sa vtedy, keď nie sú presne definované aspekty vplývajúce na proces obstarávania, teda keď sa nedajú použiť analytické metódy [7].
Heuristické metódy
Používajú sa pri rozhodovacích procesoch s vysokou mierou neurčitosti a nevyužívajú poznatky z iných vedných disciplín. Pri rozhodovacích procesoch využívajú kvalifikovaných pracovníkov alebo výpočtovú techniku. Z tohto dôvodu sa tieto modely delia do dvoch skupín: - Expertné systémy- vytvárajú tzv. predstupeň umelej inteligencie. Využívajú možnosť rýchlosti výpočtovej techniky pri spracovávaní údajov, veľkosť pamäťovej kapacity a možnosť spracovania nákupných procesov do tzv. algoritmov. Používajú sa pri rozhodovacích procesoch diagnostického alebo plánovacieho typu. - Metódy tvorivého myslenia- hlavnou úlohou je výber, pretváranie a spojovanie prvkov predchádzajúcich skúseností s procesom nákupu surovín. Využívajú sa pritom schopnosti kvalifikovaných pracovníkov [4].
Dopravné úlohy v logistike
Podľa Dupaľa (2000, s. 92) dopravné úlohy sú: „typom deterministických alokačných metód. Na ich riešenie sú vytvorené špeciálne algoritmy, pomocou ktorých sa je možno jednoduchým spôsobom dopracovať k výsledku. Hľadaným riešením je napr. určenie optimálneho množstva prepravovaného materiálu medzi dodávateľmi a spotrebiteľmi s ohľadom na kapacity dodávateľov a uspokojovanie požiadaviek spotrebiteľov tak, aby náklady na prepravu a čas prepravy boli minimálne.“ Metódy využívané pri riešení dopravných úloh v logistike:
- Metóda severozápadného rohu.
- Indexová metóda.
- Modifikovaná metóda.
- Vogelova aproximačná metóda.
- Maďarská metóda [1].
Pri riešení dopravných úloh týmito metódami sa používa nasledujúca tabuľka:
| Dodávatelia | S1 | S2 | ... | Sn | Kapacity |
|---|---|---|---|---|---|
| D1 | a1 | ||||
| D2 | a2 | ||||
| ... | ... | ||||
| Dm | am | ||||
| Požiadavky | b1 | b2 | ... | bn | Celkový súčet |
, kde: m- počet dodávateľov D n- počet spotrebiteľov S ai- kapacita i-tého dodávateľa bj- požiadavka j-tého spotrebiteľa
kde: xij- prepravované množstvo od i-tého dodávateľa j-temu spotrebiteľovi
cij- náklady na prepravu
(ui+vj)-cij- rozdiel riadkových stĺpcov a stĺpcových riadkov od prepravných nákladov (používa sa v modifikovanej metóde)
Metóda severozápadného rohu
Je to východisková metóda dopravných úloh v logistike a hoci riešenie dosiahnuté touto metódou je prijateľné, ale zďaleka nie je optimálne a konečné. Princíp spočíva v tom, že v tabuľke dopravných vzťahov začíname vypĺňaním polí od ľavého horného rohu až po pravý dolný roh, pričom sa vyčerpajú všetky kapacity dodávateľov a naplnia sa požiadavky spotrebiteľov [1].
Indexová metóda
Indexová metóda pri stanovení optimálnych prepravovaných množstiev zohľadňuje vzniknuté obstarávacie sadzby. Princíp spočíva v zoradení polí vzostupne podľa veľkosti sadzieb. Ako prvé naplníme pole s najmenšími sadzbami maximálnym možným množstvom ohraničeným kapacitou dodávateľa, resp. požiadavkou spotrebiteľa. Pokračujeme napĺňaním až po pole s maximálnymi sadzbami. Ak sa v tabuľke prepravných vzťahov nachádza viac polí s rovnakou sadzbou, uprednostníme pole, ktoré možno obsadiť väčším množstvom [1].
Modifikovaná metóda
Modifikovaná metóda je metóda riešenia dopravných vzťahov, ktorá využíva na stanovenie optimálnych prepravovaných množstiev za predpokladu minimalizácie obstarávacích nákladov stĺpcové a riadkové čísla ui a vj. Nazýva sa aj ako metóda riadkových a stĺpcových čísiel [1].
Podľa Dupaľa (2000, s. 95) sa pri riešení tejto metódy používa nasledujúci postup:
- Vypočítať stĺpcové a riadkové čísla ui a vj.
- K tabuľke pridáme stĺpec pre riadkové čísla ui, i = 1, 2...m, a riadok pre stĺpcové čísla vj, j = 1, 2...n;
- v riadku alebo v stĺpci tabuľky, kde je najviac nenulových premenných, dosadíme za ui, resp. vj nulu;
- ostatné čísla ui a vj volíme tak, aby sa súčet riadkového a stĺpcového čísla rovnal sadzbe obsadeného políčka, ktoré leží v priesečníku riadka a stĺpca, v ktorom sa tieto čísla nachádzajú.
- Vypočítať rozdiely (ui + vj) – cij pre všetky neobsadené políčka.
- Hodnotu zapísať do ľavého dolného rohu a každého neobsadeného políčka.
- Zistiť, či sú niektoré rozdiely (ui + vj) – cij kladné.
- Políčko s najväčším kladným rozdielom obsadiť maximálne možným počtom.
- Začať voľným políčkom a nájsť uzavretý okruh,
- políčka označiť striedavo znamienkami „+“ a „-“,
- najmenšiu hodnotu v políčku so znamienkom „–“ odpočítať vo všetkých políčkach so znamienkom „-“ a pripočítať vo všetkých políčkach so znamienkom „+“,
- políčka mimo uzavretého okruhu nechať bez zmeny.
- Kroky 2 až 4 opakovať až po získanie optimálneho riešenia dopravnej úlohy, t.j. bez kladných hodnôt (ui + vj) – cij.
- Určiť hodnoty účelovej funkcie Z.“
Modelovanie zásob
Podľa Ivaničovej a Brezinu (1997, s. 181): „vysoký stav zásob tovaru vo sfére výroby, ako aj v obchodnej sfére zmrazuje pohyb finančných prostriedkov, vyžaduje tvorbu nových skladovacích priestorov, resp. dochádza k znehodnoteniu dlhodobo uskladneného tovaru. Nedostatočné zásoby tovaru môžu spôsobiť zastavenie výroby, pre obchodníkov je to strata dôvery zákazníka a následné zníženie zisku. Preto výrobné podniky, ako aj obchodné organizácie sa snažia riadiť stav svojich zásob tak, aby sa zabezpečil plynulý chod výroby, resp. uspokojenie dopytu, pričom náklady na skladovanie by boli minimálne.“
Modelovanie zásob sa skladá z troch častí:
- Mechanizmus skladovania a zásobovania- ktorého cieľom je zabezpečiť čo najdokonalejšiu obsluhu za predpokladu čo najnižších nákladov. Používajú sa tu pravidlá rozhodovania, pomocou ktorých možno riadiť prevádzku zásobovacieho systému. Do tohto mechanizmu zaraďujeme nákladovo orientované modely zásob.
- Mechanizmus vstupu do systému- rieši nielen otázku spojenú s dodávkami na sklad ale aj dodacie lehoty, ktoré predstavujú časové oneskorenie medzi objednávkou a dodávkou na sklad.
- Mechanizmus výstupu zo systému- spotreba skladovaných dodávok vo forme spotreby vo vnútri podniku alebo dodávok zo skladu mimo podniku [6].
Základné pojmy
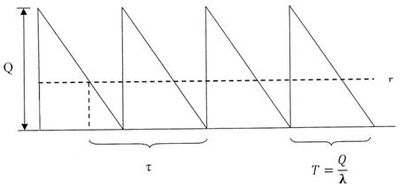
Optimálna veľkosť dodávky- symbol Q- je to množstvo tovaru potrebná na chod výroby, ktorá sa jednorázovo dodáva do skladu.
Dodávkový cyklus- symbol T- čas medzi príchodom tovaru na sklad a momentom spotrebovania všetkých zásob. Je závislí od veľkosti objednávky tovaru a intenzity čerpania zásob.
Hladina objednania- symbol r- je to hladina zásob tovaru určujúca tzv. moment objednania tr. Ak zásoby tovaru na sklade klesnú na túto hladinu (alebo pod túto hladinu), je potrebné objednať novú zásielku tovaru.
Dodacia lehota- symbol τ- časový úsek medzi momentom objednania tr a momentom príchodu objednaného tovaru na sklad. Intenzita čerpania- symbol λ- je to spotreba tovaru, závisí od nej optimálna veľkosť objednávky Q, hladina objednania r a moment objednania tr [3].
V procese modelovania zásob sa vyskytuje veľmi dôležitý pojem celkové náklady. Skladajú sa z:
- náklady skladovania- symbol cs- predstavujú všetky náklady súvisiace so skladovaním zásob a ich výška závisí od výšky skladovaného množstva,
- náklady objednávky tovaru- symbol ca- predstavujú všetky fixné náklady súvisiace s jednou objednávkou tovaru,
- náklady spojené s nedostatkom tovaru- symbol ct- nazývajú sa aj náklady deficitu,
- náklady spojené s nákupom tovaru- symbol cp- nazýva sa aj obstarávacia cena skladovaného tovaru, pretože k nákupnej cene treba prirátať na každú jednotku tovaru konštantné náklady obstarania, prípadne skladovania [3].
Klasifikácia modelov teórie zásob
Existuje niekoľko druhov členenia modelov zásob podľa viacerých hľadísk. Podľa Unčovského (1980, s. 208) sa delia nasledovne: „V prvom rade podľa typu zohľadnenia náhodných vplyvov v modeli (príp. podľa úplnosti informácií o jednotlivých veličinách) na:
- modely deterministické,
- modely stochastické.
Podľa spôsobu zohľadnenia vývoja spotreby v čase na:
- Modely statické, ktoré berú do úvahy len jediný dodávkový cyklus (čas medzi dodaním dodávky na sklad a jej spotrebu).
- Modely dynamické, ktoré berú do úvahy viac následných dodávkových cyklov. Tieto modely sa ďalej delia podľa stacionárnosti spotreby na:
- modely stacionárne, kde sa spotreba v jednotlivých cykloch nemení,
- modely nestacionárne, kde sa priemerná hodnota mení medzi jednotlivými cyklami.
Podľa spojitosti spotreby sa rozlišujú:
- modely so spojitou spotrebou,
- modely s nespojitou spotrebou.
Podľa spôsobu riešenia vyčerpania sa rozlišujú:
- modely s odkladom,
- modely so stratenými predajmi.
Podľa počtu skladových substrátov sa rozlišujú:
- modely jednoprvkové, pri ktorých sa berie do úvahy len skladovanie jediného substrátu,
- modely viacprvkové, pri ktorých sa skladajú viaceré substráty.
Podľa počtu skladov sa rozlišujú:
- systémy s jedným skladom,
- systémy s viacerými skladmi.“
Ivaničová a Brezina (1997, s. 185) vo svojej publikácií doplnili nasledujúce členenie modelov zásob: „Podľa dĺžky možnej skladovateľnosti tovarov rozoznávame:
- Modely s neohraničenou skladovateľnosťou.
- Modely s ohraničenou skladovateľnosťou.
Na základe ovládateľnosti modelovaných veličín rozlišujeme:
- Modely s ovládaným doplňovaním zásob:
- s voľnými objednávacími termínmi,
- s pevnými objednávacími termínmi.
- Modely s neovládaným doplňovaním zásob:
Dôležitým ukazovateľom pri tvorbe modelov zásob je počet dodávkových cyklov za skúmané obdobie. Podľa toho rozlišujeme:
- Zásoby s vysokou obrátkou (s častou spotrebou).
- Zásoby s nízkou obrátkou (so zriedkavou spotrebou).“
Deterministické modely zásobovania
Z historického hľadiska sú deterministické modely najstaršie typy modelov zásob. Vznikli v snahe zracionalizovať proces nákupu použitím rôznych matematických vzorcov a metód na určovanie optimálnej výšky dodávky na sklad. Vychádzajú z dvoch základných predpokladov:
- úplnej informovanosti – znalosť všetkých veličín modelu (viď 2.4.1),
- úplnej ovládateľnosti – možnosť určenia potrebnej výšky a časového rozdelenia veličín [6].
Model optimálnej veľkosti dodávky so spojitou spotrebou
Tento model patrí k základným typom deterministických modelov a vychádza z nasledujúcich predpokladov:
- Intenzita čerpania λ- resp. spotreba má počas celého roka, ktorý je základné plánovacie obdobie, rovnomerný charakter.
- Dodacia lehota τ- je počas celého roka konštantná.
- Optimálna veľkosť dodávky Q- nie je ohraničená a moment doručenia objednávky na sklad si môžeme zvoliť, pričom všetky dodávky zásob sa uskutočňujú naraz.
- Deficit zásob nie je možné dosiahnuť a vzhľadom nato, že model optimálnej veľkosti dodávky so spojitou spotrebou je model stacionárny, výška dodávky a čas jej dodania sú vždy tie isté [6].
Dodávkový cyklus T- je charakterizovaný ako rozdiel času medzi dvoma po sebe nasledujúcimi dodávkami a vypočítame ho nasledovne [6]:
Dodávkový cyklus je graficky znázornený na obr. 6.
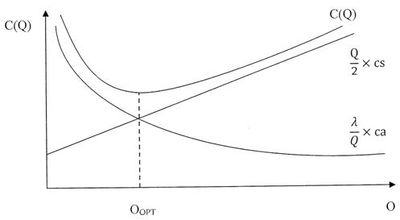
Výsledná nákladová funkcia C(Q)
Na určenie optimálnej veľkosti dodávky na sklad potrebujeme poznať nákladovú funkciu (obr. 7). Je to funkcia celkových nákladov za určité obdobie. Celkové náklady pri tom pozostávajú z:
- náklady objednávky tovaru ca,
- náklady skladovania cs.
Výsledná nákladová funkcia má tvar [6]:
Na obr. 7 je optimálna veľkosť dodávky QOPT znázornená ako jediné absolútne minimum výslednej nákladovej funkcie. Nazýva sa aj Wilsonov vzorec, a má tvar [6]:
Elementárny model s deficitom
Deterministické modely nepripúšťajú možnosť vzniku deficitu zásob, ale elementárny model s deficitom je chápaný ako náhrada za stochastické modely, tak túto možnosť má. Rozlišujú sa modely s deficitom:
- s odloženou spotrebou- vystupujú tu dva typy nákladov deficitu:
- náklady závislé od množstva a času,
- náklady závislé len od množstva;
- so stratenou spotrebou [6].
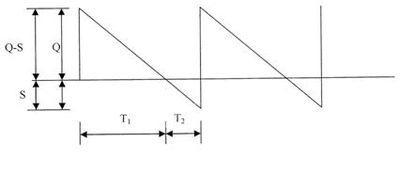
K elementárnym modelom zásob s deficitom patrí predovšetkým model s nákladmi deficitu závislými od množstva a času ct. Tento model má rovnaké predpoklady ako model optimálnej veľkosti dodávky so spojitou spotrebou, okrem predpokladu vzniku deficitu zásob a dopĺňajú ho nasledujúce predpoklady:
- Spotreba zásob je v období T1 krytá, v období T2 sa zásoby minú a tak nie je možné uspokojiť spotrebu v nasledujúcom období. Tento stav je znázornený na obr. 8.
- Vznik nákladov deficitu ct.
- V tomto modely vzniká tzv. výška neuspokojenej spotreby s. Chápe sa aj ako potrebné množstvo zásob v sklade na zabránenie vzniku deficitu. Je to tzv. poistná zásoba [6].
Výsledná nákladová funkcia C(Q,s)
Má podobný charakter ako nákladová funkcia modelu optimálnej veľkosti dodávky so spojitou spotrebou, rozdiel je len v tom, že v tomto modelu je funkcia dvoch premenných Q a s. Celkové náklady pozostávajú okrem nákladov objednávky tovaru ca a nákladov skladovania tovaru cs aj z nákladov deficitu ct.
Má tvar [6]:
Výška optimálnych dodávok na sklad QOPT Nájdením absolútneho minima výslednej nákladovej funkcie dvoch premenných Q a s môžeme vyjadriť vzťah [6]:
Podobný vzorec stanovenia optima sa používa aj pri stochastických modeloch, kde sa vzorec pre optimálnu dodávku násobí poistným koeficientom [6]:
Výška optimálnej poistnej zásoby [6]:
Stochastické modely zásobovania
V reálnych zásobovacích systémoch majú viaceré veličiny a vzťahy v skutočnosti stochastický charakter, čo znamená, že sa viac približujú realite ako deterministické modely, ktoré veľmi zjednodušujú skutočnosť. Stochastické modely sa zakladajú na aplikácií počtu pravdepodobnosti a najčastejšie sa používajú na optimalizáciu určitej účelovej funkcie, napr. na optimalizáciu zásobovacích činností [6].
V procese zásobovania sa vyskytujú tri stochastické prvky: - spotreba- stochastická vo výške a v čase, - dodacia lehota- vystupuje ako náhodná premenná, - veľkosť dodávky na sklad [6].
Stochastické modely sa väčšinou spájajú s možným rizikom vzniku vyčerpania zásob (deficit), preto sa musí vytvárať tzv. poistná zásoba. Plánovanie relatívne vysokých poistných zásob vedie k eliminácií možnosti vyčerpania zásob [6].
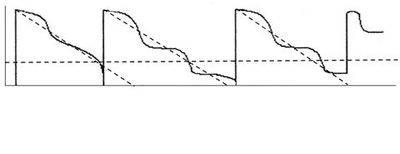
Členenie stochastických modelov: 1) Systémy so signalizáciou zmien- princíp evidencie a porovnávania každej zmeny stavu zásob v sklade s kritickými hladinami zásob. Patria sem:
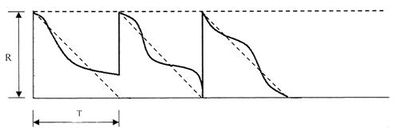
a) Stochastický model optimálnej veľkosti dodávok (model Q, r)- princíp tohto modelu spočíva v stanovení optimálnej veľkosti dodávky QOPT a hladiny objednania r a ako náhle stav zásob klesne na hladinu r, objedná sa optimálna dodávka QOPT. Dodávkový cyklus T sa v jednotlivých cykloch odlišuje [6].
Graficky sa znázorňuje:
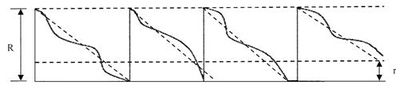
b) Stochastický model dvoch zásobníkov (model R, r)- má podobný princíp ako predchádzajúci model. Vyskytuje sa tu okrem dolnej hranice objednania r aj horná hranica objednania R, na ktorú sa zásoby v sklade doplnia v prípade dosiahnutia hranice r. To má za dôsledok rovnaký stav zásob v sklade na začiatku každého obdobia [6].
Graficky sa znázorňuje:
2. Systémy s periodickou kontrolou- princíp využívania periodických stratégií. Zásobovací systém predpokladá, že zaznamenávanie každej zmeny stavu zásob v sklade je náročný proces, tak ju porovnáva s hladinami objednania len v určitých, periodicky sa opakovaných okamihoch. Patria sem:
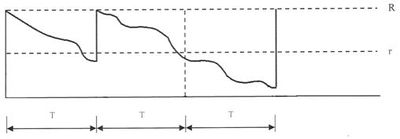
a) Cyklický model zásob (model R, T)- princíp stanovenia optimálnej dĺžky kontrolného cyklu. Vždy na konci tohto kontrolného cyklu sa dopĺňa stav zásob v sklade až po hornú hladinu objednania R, pričom sa neberie ohľad na momentálnu výšku zásob v sklade. Dodávkový cyklus T zostáva konštantný, mení sa len objednávané množstvo tovaru [6].
Graficky sa znázorňuje:
b) Periodický model dvoch zásobníkov (model R, r, T)- funguje na podobnom princípe ako predchádzajúci model. Rozdiel je len v tom, že na konci kontrolného cyklu sa porovná momentálny stav zásob v sklade s dolnou hladinou objednania r a pri jej prekročení sa objednáva množstvo tovaru až po hladinu R [6]. Graficky sa znázorňuje:
Stochastický model optimálnej veľkosti dodávok
Tento model je v podstate stochastický variant deterministických modelov využívaný v prípadoch s nekonštantným dodávkovým cyklom T. Stochastický model (Q, r) nahrádza poistnú zásobu s hladinou objednania r. Predpoklady jeho použitia sú nasledujúce:
- Deficit zásob je možné dosiahnuť a vzniká len jeden typ nákladov deficitu, a to náklady deficitu závislé len od množstva cd.
- Spotreba zásob je stochastická; známa hustota f (x; t) pravdepodobnosti že spotreba zásob je v čase t medzi x a x + dx; stredná hodnota stacionárnej spotreby zásob je rovné intenzite čerpania λ.
- Zásoby na ceste nie sú väčšie ako jedna dodávka zásob.
- Hodnota zásob a všetkých druhov nákladov s nimi spojenými nie sú závislé od veľkosti dodávky Q a od hladiny objednania r.
- Vo všetkých dodávkových cykloch je hladina objednania r kladná.
- Dodacia lehota nadobúda podobu:
- deterministickej veličiny,
- alebo stochastickej spojitej veličiny [6].
Výsledná nákladová funkcia C(Q, r) Na rozdiel od deterministických modeloch má tvar strednej hodnoty všetkých nákladov za určitý cyklus. Vyskytujú sa tu:
- náklady dodávky ca,
- náklady skladovania cs,
- a náklady deficitu ct.
Má tvar [6]:
, kde d ̅ je stredná hodnota deficitu a E(x) spotreba počas dodacej lehoty.
Výška optimálnej dodávky na sklad QOPT [6]:
Hladina objednania r [6]: