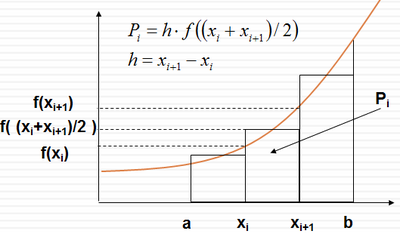Java - algoritmy numerického integrovania
Základy informatiky - jazyk Java
Úvod do programovania v jazyku Java
Java - objektovo orientovaný prístup
Vzorové príklady:
Java - implementácia numerických algoritmov
- >Java - algoritmy hľadania nulových miest
>Java - algoritmy numerického derivovania
>Java - algoritmy numerického integrovania
>Java - algoritmy aproximácie
>Java - algoritmy interpolácie
Java - triedy geometrických tvarov
Pokročilé témy:
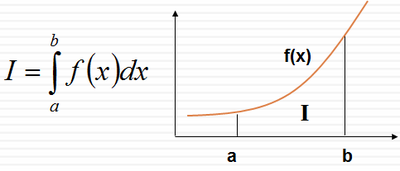
Ďalšími numerickými algoritmami sú algoritmy numerického integrovania. Pri výpočte integrálu pomocou numerických metód vychádzame z faktu, hodnota určitého integrálu je plocha pod krivkou (definuje je integrovaná funkcia), ohraničená hranicami integrovania.
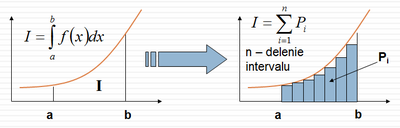
Túto často nepravidelnú plochu si rozdelíme na také časti, ktorých plochu vieme spočítať a potom všetky tieto časti sčítame.
Podľa spôsobu rozdelenia celej plochy na jednotlivé časti poznáme metódy výpočtu určitého integrálu:
- Obdĺžniková metóda
- Lichobežníková metóta
- Simpsonova metóda
Obsah
Obdĺžniková metóda
Pri tejto metóde si plochu rozdelíme na obdĺžniky, ako to ukazuje nasledujúci obrázok:
Integrál, ktorý počítame môžeme zapísať nasledovne:
[math]\begin{align}
& I=\int\limits_{a}^{b}{f\left( x \right)dx}=\sum\limits_{i=0}^{n-1}{{{P}_{i}}}=\sum\limits_{i=0}^{n-1}{h\cdot f\left( \frac{{{x}_{i}}+{{x}_{i+1}}}{2} \right)}=h\sum\limits_{i=0}^{n-1}{f\left( \frac{{{x}_{i}}+{{x}_{i+1}}}{2} \right)} \\
& kde\,h=\frac{b-a}{n} \\
\end{align}[/math]
Všimnite si, že výška jedného obdĺžnika sa vypočíta ako aritmetický priemer susedných funkčných hodnôt.
Implementácia v Jave
Triedu Solver doplníme o metódu integralObdlznik:
public double integralObdlznik(double a, double b, int n) {
double krok = (b - a) / n;
double I = 0, x;
for (x = a; x < b; x += krok) {
I += this.f.hodnota((2 * x + krok) / 2);
}
return I * krok;
}
Lichobežníková metóda
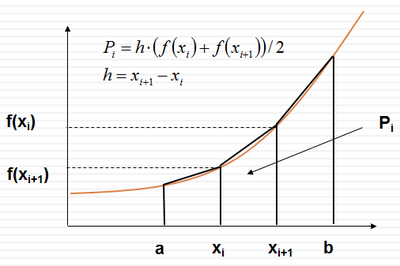
Táto metóda je veľmi podobná predchádzajúcej, ale plochu nerozdelíme na obdĺžniky, ako na lichobežníky:
Integrál, ktorý počítame môžeme zapísať nasledovne:
[math]\begin{align}
& I=\int\limits_{a}^{b}{f\left( x \right)dx}=\sum\limits_{i=0}^{n-1}{{{P}_{i}}}=\sum\limits_{i=0}^{n-1}{h\cdot \frac{f\left( {{x}_{i}} \right)+f\left( {{x}_{i+1}} \right)}{2}}=\frac{h}{2}\sum\limits_{i=0}^{n-1}{\left( f\left( {{x}_{i}} \right)+f\left( {{x}_{i+1}} \right) \right)}=h\left( \frac{1}{2}f\left( {{x}_{0}} \right)+\sum\limits_{i=1}^{n-2}{f\left( {{x}_{i}} \right)+\frac{1}{2}f\left( {{x}_{n-1}} \right)} \right) \\
& kde\,h=\frac{b-a}{n} \\
\end{align}[/math]
Implementácia v Jave
Triedu Solver doplníme o metódu integralLichobeznik:
public double integralLichobeznik(double a, double b, int n) {
double krok = (b - a) / n;
double I = 0, x;
for (x = a + krok; x < b - krok; x += krok) {
I += this.f.hodnota(x);
}
I += (this.f.hodnota(a) + this.f.hodnota(b)) / 2;
return I * krok;
}
Simpsonova metóda
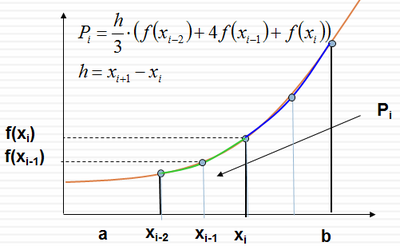
Táto metóda je presnejšia, ale výpočet trvá dlhší čas. Časti, na ktoré rozdelíme plochu budú zhora ohraničené parabolou. Obsah časti zhora ohraničenej parabolou je na nasledujúcom obrázku.
Integrál, ktorý počítame môžeme zapísať nasledovne:
[math]\begin{align}
& I=\int\limits_{a}^{b}{f\left( x \right)dx}=\sum\limits_{i=a}^{b}{{{P}_{i}}}=\sum\limits_{i=a}^{b}{\frac{h}{3}\cdot \left( f\left( {{x}_{i-2}} \right)+4f\left( {{x}_{i-1}} \right)+f\left( {{x}_{i}} \right) \right)}=\frac{h}{3}\sum\limits_{i=a}^{b}{f\left( {{x}_{i-2}} \right)+4f\left( {{x}_{i-1}} \right)+f\left( {{x}_{i}} \right)} \\
& kde\,h=\frac{b-a}{n} \\
\end{align}[/math]
Implementácia v Jave
Triedu Solver doplníme o metódu integralSimpson:
public double integralSimpson(double a, double b, int n) {
double krok = (b - a) / n;
double I = 0, x;
for (x = a + 2 * krok; x <= b; x += 2 * krok) {
I += (this.f.hodnota(x - 2 * krok) + 4 * this.f.hodnota(x - krok) + this.f.hodnota(x));
}
return I * krok / 3;
}
Implementácia algoritmov numerického integrovania v Java aplikácii
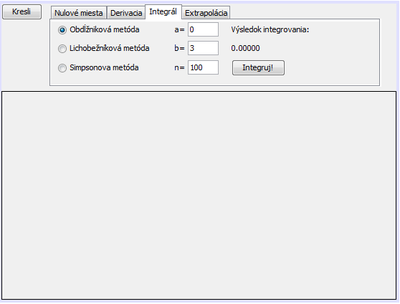
Vo vzorovej aplikácii pridáme na kartu 'Integrál' komponenty podľa nasledujúceho obrázku:
Opis komponentov:
buttonGroup
- do aplikácie pridáme nevizuálny komponent buttonGroup
- názov komponentu integralGroup
RadioButton
- Obdĺžniková metóda
- názov komponentu rbObdlznik,
- vlastnosť buttonGroup: integralGroup
- Lichobežníková metóta
- názov komponentu rbLichobeznik,
- vlastnosť buttonGroup: integralGroup
- Simpsonova metóda
- názov komponentu rbSimpson,
- vlastnosť buttonGroup: integralGroup
textField
- zadávanie začiatku intervalu integrovania : a
- názov komponentu: textIntegralA
- zadávanie konca intervalu integrovania : b
- názov komponentu: textIntegralB
- zadávanie hodnoty n - delenie intervalu
- názov komponentu: textIntegralN
label
- text, pre zobrazenie výsledku integrovania (na obrázku 0.00000)
- názov komponentu: labelntegralVysledok
- prednastavený text komponentu: 0.00000
button
- tlačidlo 'Integruj!' slúži na spustenie výpočtu integrálu
- názov komponentu: btnIntegruj
- udalosť tlačidla: actionPerformed
Obsluha tlačítka 'Integruj!':
private void btnIntegrujActionPerformed(java.awt.event.ActionEvent evt) {
double a, b, I = 0;
int n;
a = Double.valueOf(textIntegralA.getText());
b = Double.valueOf(textIntegralB.getText());
n = Integer.valueOf(textIntegralN.getText());
if (rbObdlznik.isSelected()) {
I = this.s.integralObdlznik(a, b, n);
}
if (rbLichobeznik.isSelected()) {
I = this.s.integralLichobeznik(a, b, n);
}
if (rbSimpson.isSelected()) {
I = this.s.integralSimpson(a, b, n);
}
labelntegralVysledok.setText(String.valueOf(I));
}
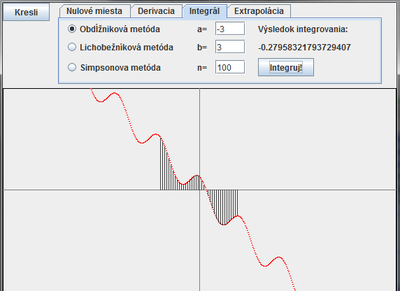
Vizualizácia vypočítané integrálu
Do aplikácie doplníme zobrazenie hraníc integrálu a plochu pod integrovanou krivkou vyšrafujeme. Šrafovanie bude pozdĺžne. Budeme teda na intervale <a,b> kresliť zvislé čiary. Doplníme predchádzajúcu metódu:
private void btnIntegrujActionPerformed(java.awt.event.ActionEvent evt) {
double a, b, I = 0;
int n;
a = Double.valueOf(textIntegralA.getText());
b = Double.valueOf(textIntegralB.getText());
n = Integer.valueOf(textIntegralN.getText());
if (rbObdlznik.isSelected()) {
I = this.s.integralObdlznik(a, b, n);
}
if (rbLichobeznik.isSelected()) {
I = this.s.integralLichobeznik(a, b, n);
}
if (rbSimpson.isSelected()) {
I = this.s.integralSimpson(a, b, n);
}
labelntegralVysledok.setText(String.valueOf(I));
//srafovanie
g.setColor(Color.DARK_GRAY);
double x,y,krok;
krok=t.getKrok()*3;
for(x=a;x<b;x+=krok){
y=f.hodnota(x);
g.drawLine(t.getX(x),t.getY(0) ,t.getX(x), t.getY(y));
}
}
Výsledok: