Java - algoritmy numerického derivovania
Základy informatiky - jazyk Java
Úvod do programovania v jazyku Java
Java - objektovo orientovaný prístup
Vzorové príklady:
Java - implementácia numerických algoritmov
- >Java - algoritmy hľadania nulových miest
>Java - algoritmy numerického derivovania
>Java - algoritmy numerického integrovania
>Java - algoritmy aproximácie
>Java - algoritmy interpolácie
Java - triedy geometrických tvarov
Pokročilé témy:
Medzi ďalšie numerické algoritmy patria algoritmy numerického derivovania. Nasledujúce algoritmy budeme dopĺňať do triedy Solver. V nasledujúcom texte budú ukázané 2 metódy numerického derivovania. Prvá metóda je priamo odvodená z definície derivácie a druhá metóda používa rozdielové diferencie.
Obsah
Algoritmy numerického derivovania
Základná numerická derivácia
Drivácia funkcie f(x) je definovaná ako:
[math]{f}'\left( x \right)=\underset{h\to 0}{\mathop{\lim }}\,\frac{f\left( x+h \right)-f\left( x \right)}{h}[/math]
Z tejto definíce budeme vychádzať aj pri implementácii algoritmu derivovania. Limitu v predchádzajúcom vzorci nahradíme tým, že do premennej h dosadíme hodnotu blížiacu sa k nule.
V triede Solver sme doplnili premennú h, ktorej význam je najlepšie vidieť z predchádzajúceho vzorca. V nasledujúcom zdrojovom kóde je uvedený aj konštruktor triedy Solver, v ktorom je doplnená inicializácie premennej h. Ešte poznamenajme, že počítame deriváciu funkcie f, ktorá je členským objektom v triede Solver.
public class Solver {
private FunkceM f;
public double h;
public Solver(FunkceM f) {
this.f = f;
this.h = 0.0000001;
}
//...
public double derivacia1(double x0) {
return (this.f.hodnota(x0 + this.h) - this.f.hodnota(x0)) / this.h;
}
//...
}
Derivácia pomocou rozdielových diferencií
Prvá derivácie funkcie f(x) sa dá definovať aj nasledovne:
[math]{f}'\left( {{x}_{0}} \right)=\frac{1}{h}\left( \frac{\Delta {{y}_{-1}}+\Delta {{y}_{1}}}{2}-\frac{1}{6}\frac{{{\Delta }^{3}}{{y}_{-1}}-{{\Delta }^{3}}{{y}_{1}}}{2} \right)[/math]
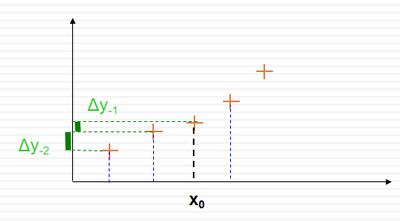
kde [math]\Delta{y}[/math] sú rozdielové diferencie. Tieto diferencie sa dajú znázorniť nasledovne:
Pre výpočet jednotlivých diferencií je potrebné poznať hodnotu h. Jej význam je rovnaký ako v predchádzajúcom príklade. Pre výpočet diferencií platia vzťahy:
[math]\begin{align}
& \Delta {{y}_{-2}}=f\left( {{x}_{0}}-h \right)-f\left( {{x}_{0}}-2h \right) \\
& \Delta {{y}_{-1}}=f\left( {{x}_{0}} \right)-f\left( {{x}_{0}}-h \right) \\
& \Delta {{y}_{1}}=f({{x}_{0}}+h)-f\left( {{x}_{0}} \right) \\
& \Delta {{y}_{2}}=f({{x}_{0}}+2h)-f\left( {{x}_{0}}+h \right) \\
\end{align}[/math]
[math]\begin{align}
& {{\Delta }^{2}}{{y}_{-1}}=\Delta {{y}_{-1}}-\Delta {{y}_{-2}} \\
& {{\Delta }^{2}}{{y}_{0}}=\Delta {{y}_{1}}-\Delta {{y}_{-1}} \\
& {{\Delta }^{2}}{{y}_{1}}=\Delta {{y}_{2}}-\Delta {{y}_{1}} \\
\end{align}[/math]
[math]\begin{align}
& {{\Delta }^{3}}{{y}_{-1}}={{\Delta }^{2}}{{y}_{0}}-{{\Delta }^{2}}{{y}_{-1}} \\
& {{\Delta }^{3}}{{y}_{1}}={{\Delta }^{2}}{{y}_{1}}-{{\Delta }^{2}}{{y}_{0}} \\
\end{align}[/math]
[math]{{\Delta }^{4}}{{y}_{0}}={{\Delta }^{3}}{{y}_{1}}-{{\Delta }^{3}}{{y}_{-1}}\,[/math]
Na nasledujúcom obrázku je znázornený geometrický význam rozdielových diferencií.
Triedu Solver doplníme nasledovne:
public double derivacia2(double x0) {
double delta[] = new double[5];
delta[0] = this.f.hodnota(x0 - 2 * this.h);
delta[1] = this.f.hodnota(x0 - this.h);
delta[2] = this.f.hodnota(x0);
delta[3] = this.f.hodnota(x0 + this.h);
delta[4] = this.f.hodnota(x0 + 2 * this.h);
// vypocet delta
for (int i = 0; i < 4; i++) {
delta[i] = delta[i + 1] - delta[i];
}
double derivace = (delta[1] + delta[2]) / 2;
// vypocet delta^2
for (int i = 0; i < 3; i++) {
delta[i] = delta[i + 1] - delta[i];
}
// vypocet delta^3
for (int i = 0; i < 2; i++) {
delta[i] = delta[i + 1] - delta[i];
}
derivace -= (delta[0] - delta[1]) / 12;
return derivace / this.h;
}
Poznámky k zdrojovému kódu:
- pre výpočet diferencií [math]\Delta{y}[/math] sme použili jednorozmerné pole derivace
- v jednotlivých cyklch for počítame [math]\Delta{y}[/math], [math]\Delta^2{y}[/math] a [math]\Delta^3{y}[/math]
- V poslednom kroku dosad9me diferencie do vzorca na výpočet derivácie.
Použitie metód derivácie v aplikácii
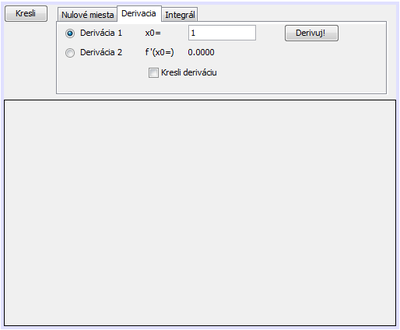
Vo vzorovej aplikácii pridáme na kartu 'Drivácia' komponenty podľa nasledujúceho obrázku:
Opis komponentov:
buttonGroup
- do aplikácie pridáme nevizuálny komponent buttonGroup
- názov komponentu derivaciaGroup
RadioButton
- Derivácia 1:
- názov komponentu rbDerivacia1,
- vlastnosť buttonGroup: derivaciaGroup
- Derivácia 2:
- názov komponentu rbDerivacia2
- vlastnosť buttonGroup: derivaciaGroup
textField
- Slúži na zadanie bodu x0, v ktorom budeme počítať deriváciu
- názov komponentu: textX0
label
- Zobrazenie výsledku derivácie (je pod komponentom textX0). Na predchádzajúcom obrázku má hodnotu 0.000 .
- názov komponentu: labelDerivacia
- Ostatné komponenty label slúžia iba na zobrazenie textu, ktorý sa počas behu programu nemení.
button
- tlačidlo 'Derivuj!' slúži na spustenie výpočtu derivácie
- názov komponentu: btnDerivuj
- udalosť tlačidla: actionPerformed
checkBox
- Zaškrtávacie tlačidlo využijeme pri možnsti vykresliť priebeh derivácie
- názov komponentu: cbKresliDerivaciu
Obsluha tlačítka 'Derivuj!':
private void btnDerivujActionPerformed(java.awt.event.ActionEvent evt) {
double x0 = Double.valueOf(textX0.getText());
if (rbDerivacia1.isSelected()) {
x0 = s.derivacia1(x0);
}
if (rbDerivacia1.isSelected()) {
x0 = s.derivacia2(x0);
}
labelDerivacia.setText(String.valueOf(x0));
}
Vykreslenie priebehu derivácie.
Zmena, resp. doplnenie kódu bude v metóde tlcKresliActionPerformed, ktorá sa stará o vykreslenie matematickej funkcie. V nasledujpcom zdrojovom kóde je uvedený výpis celej metódy tlcKresliActionPerformed.
private void tlcKresliActionPerformed(java.awt.event.ActionEvent evt) {
int sirka, vyska; //sirka a vyska panelu na kreslenie
sirka = panel.getWidth();
vyska = panel.getHeight();
t.setSize(sirka, vyska);
g = panel.getGraphics();
g.setColor(Color.GRAY);
g.drawLine(0, vyska / 2, sirka, vyska / 2);
g.drawLine(sirka / 2, 0, sirka / 2, vyska);
g.setColor(Color.RED);
double x1, y1, x2, y2 = 0;
int X1, Y1, X2, Y2;
x1 = -t.getStrana();
y1 = f.hodnota(x1);
for (x2 = -t.getStrana(); x2 < t.getStrana(); x2 += t.getKrok()) {
y2 = f.hodnota(x1);
X1 = t.getX(x1);
X2 = t.getX(x2);
Y1 = t.getY(y1);
Y2 = t.getY(y2);
g.drawLine(X1, Y2, X2, Y2);
x1 = x2;
y1 = y2;
}
// doplnenie vykreslovania priebehu prvej derivacie
if (cbKresliDerivaciu.isSelected()) {
g.setColor(Color.ORANGE);
x1 = -t.getStrana();
y1 = s.derivacia2(x1);
for (x2 = -t.getStrana() + t.getKrok(); x2 < t.getStrana(); x2 += t.getKrok()) {
if (rbDerivacia1.isSelected()) {
y2 = s.derivacia1(x2);
}
if (rbDerivacia2.isSelected()) {
y2 = s.derivacia2(x2);
}
g.drawLine(t.getX(x1), t.getY(y1), t.getX(x2), t.getY(y2));
x1 = x2;
y1 = y2;
}
}
}
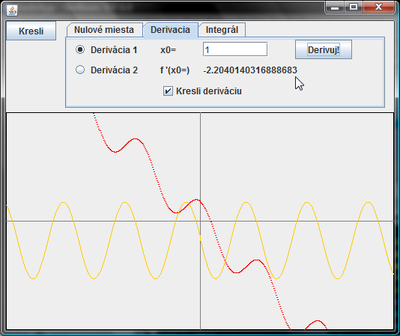
Na nasledujúcom obrázku je červenou farbou nakreslená funkcia [math]cos(2x)-x[/math] a oranžovou farbou je vykreslená prvá derivácia.