Java - algoritmy hľadania nulových miest

Z Kiwiki
Skočit na navigaci Skočit na vyhledávání

Základy informatiky - jazyk Java

Platforma Java - prehľad

Úvod do programovania v jazyku Java

Java - objektovo orientovaný prístup

Vzorové príklady:

Prvé programy v Jave

Vzorové triedy v Jave

Java applety

Java - desktopové aplikácie

Java - implementácia numerických algoritmov

>Java - algoritmy hľadania nulových miest
>Java - algoritmy numerického derivovania
>Java - algoritmy numerického integrovania
>Java - algoritmy aproximácie
>Java - algoritmy interpolácie

Java - triedy geometrických tvarov

Pokročilé témy:

Základy práce s NetBeans IDE a vývoj modulov

Algoritmy hľadania nulových miest (A root-finding algorithms), sú také algoritmy ktoré hľadajú takú hodnotu x, pre ktorú platí f(x)=0, pre danú funkcie f.

Hľadanie nulových miest rovnice [math]f(x) − g(x) = 0[/math] je totožné s riešením rovnice [math]f(x) = g(x)[/math], kde x je neznáma. Inak povedané, ľubovoľnú rovnicu môžeme vyjadriť v kanonickom tvare [math]f(x) = 0[/math], takže riešenie takejto rovnice je vlastne hľadaním nulového bodu funkcie. Prvý odhad riešenia rovnice je počiatočný návrh. Zvolená metóda (algoritmus) vypočítava postupnosť hodnôt, ktoré berú v ohľad predchádzajúcu vypočítanú hodnotu a riešenú funkciu f.

Newtonova metóda nulových miest

Pre danú funkciu [math]f(x)[/math] a je algoritmus definovaný pomocou vzorca

[math]x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}. \,\![/math]

kde

[math]{f'(x_n)}. \,\![/math] je prvá derivácia funkcie [math]{f(x_n)}. \,\![/math]

Hodnota [math]x_0[/math] je prvý odhad riešenia. Výpočet skončíme vtedy, keď sa hodnota [math]{f(x_n)}. \,\![/math] blíži k nule.

Podrobnejšie o Newtonovom algoritme hľadania nulových miest je v článku Algoritmy hľadania nulových miest#Newtonova metóda nulových miest

Metóda polenia intervalov

Podrobnejšie o algoritme polenia intervalu je v článku Algoritmy hľadania nulových miest#Metóda polenia intervalov

Riešenie v jave

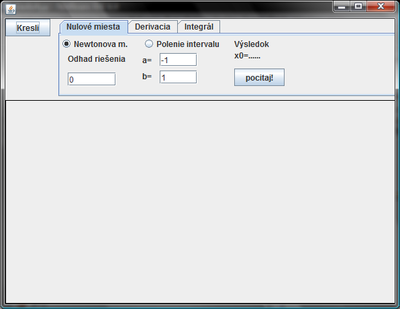
V tejto časti budeme pokračovať v aplikácii, ktorú sme si navehli v časti Java (Swing) - práca s vizuálnymi komponentami#Práca so záložkami. Prvú záložky pomenujeme 'Nulové miesta' a vložíme na ňu nasledujúce komponenty:

  • jButtonGroup - dovolí výber len jednej možnosti
    • názov komponentu: skupinaNuloveBody
  • jRadioButton - možnosť výberu Newtonovej metódy výpočtu nulového miesta.
    • názov komponentu: rbNewton
    • Text komponentu: 'Newtonova m.'
    • vlastnosť selected: true
    • vlastnosť buttonGroup: skupinaNuloveBody
  • jRadioButton - možnosť výberu metódy polenia intervalu pre výpočet nulového miesta.
    • názov komponentu: rbPolenie
    • Text komponentu: 'Newtonova m.'
    • vlastnosť buttonGroup: skupinaNuloveBody
  • jTextField - textové políčko pre vloženie odhadu riešenie pri Newtonovej metóde
    • Názov kompoentu: textOdhadX
    • Text komponentu: '0'
  • jTextField - textové políčko pre vloženie bodu A pri metóde polenia intervalu
    • Názov kompoentu: textPolenieA
    • Text komponentu: '-1'
  • jTextField - textové políčko pre vloženie bodu B pri metóde polenia intervalu
    • Názov kompoentu: textPolenieB
    • Text komponentu: '1'
  • jlabel - texttový objekt, do ktorého vpíšeme výsledok riešenia
    • Názov kompoentu: labelX0
    • Text komponentu: 'x0=...'
  • jButton - tlačidlo pre spustenie algoritmu výpočtu nulových bodov.
    • Názov kompoentu: tlcNula
    • Text komponentu: 'pocitaj!'
Návrh dizajnu aplikácie pre výpočet nulových miest.

Úprava triedy Function.java

Nevýhodou newtonovej metódy je fakt, že potrebuje mať k dispozícii prvú deriváciu funkcie pre ktorú hľadnáme nulový bod. Doplňme teda do triedy Function.java metódu derivacia: 

public class Function {

    private double a, b, c;

    // vsetky ostatne metody su uvedene v predchadzajucom texte

    public double hodnota(double x) {
        return a * Math.cos(b * x) - Math.pow(x, c);
    }

    public double derivacia(double x) {
        return -a * b * Math.sin(b * x) - c * Math.pow(x, c - 1);
    }
}

Úprava triedy Solver.java

Do triedy doplníme 2 nové metody, ktoré budú implementovať 2 numerické algoritmy hľadania nulových miest.


Newtonova metóda nulových miest

Túto metódu budeme implementovať pomocou rekurizie. Rekurzia je vysvetľovaná v článku Rekurzia.


Metóda polenia intervalov

V článku Algoritmy hľadania nulových miest#Metóda polenia intervalov je uvedený zdrojový kód v jazyku C. Tento zdrojový kód je na 95% podobý zdrojovému kódu v Jave. Preto použijeme tento zdrojový kód a upravíme ho do syntaxe jazyka Java.

V nasledujúcom výpise sú uvedené len nové metódy triedy Solver: 

package numeric;

public class Solver {

    private Function f;
    private double presnost;

    public double nulaNewton(double x0) {
        if (Math.abs(this.f.hodnota(x0)) < this.presnost) {
            return x0;
        } else {
            return nulaNewton(x0 - f.hodnota(x0) / f.derivacia(x0));
        }
    }

    public double nulaPolenie(double a, double b) {
        // predpoklad správneho riesenia:
        // jedna z hodnot f(a),f(b) musi byt mensia ako 0, druha vacsia ako 0
        double lo, hi, mid;
        if (this.f.hodnota(a) <= 0) {
            lo = a;
            hi = b;
        } else {
            lo = b;
            hi = a;
        }
        mid = lo + (hi - lo) / 2;
        while ((mid != lo) && (mid != hi)) {
            if (this.f.hodnota(mid) <= 0) {
                lo = mid;
            } else {
                hi = mid;
            }
            mid = lo + (hi - lo) / 2;
        }
        return mid;
    }
}

Použitie algoritmov v programe

Komponentu tlcNula pridáme udalosť actionPerformed, v ktorej bude výpočet nulového miesta pre funkciu definovanú v triede Function. 

    private void tlcNulaActionPerformed(java.awt.event.ActionEvent evt) {
        double h1=0,h2 = 0;
        if(rbNewton.isSelected()){
            h1=Double.valueOf(textOdhadX.getText());
            h1=s.nulaNewton(h1);
        }
        if(rbPolenie.isSelected()){
            h1=Double.valueOf(textPolenieA.getText());
            h2=Double.valueOf(textPolenieB.getText());
            h1=s.nulaPolenie(h1, h2);
        }
        labelX0.setText(String.valueOf(h1));
    }

Poznámky k zdrojovému kódu:

  • Newtonova metóda potrebuje odhad správneho riešenia:
    • túto hodnotu získame z komponentu textOdhadX a uložíme ju do premennej h1.
    • do premennej h1 uložíme výsledok, ktorý nám vráti metóda nulaNewton
  • Metóda polenia intervalu potrebuje 2 hodnoty: bod v ktorom má funkcia zápornú hodnotu a bod v ktorom má kladnú hodnotu
    • tieto hodnoty získame z komponentov textPolenieA a textPolenieB. Hodnoty uložíme do premenných h1 a h2.
    • do premennej h1 uložíme výsledok, ktorý nám vráti metóda nulaPolenie
  • výsledok vypíšeme do komponentu labelX0.

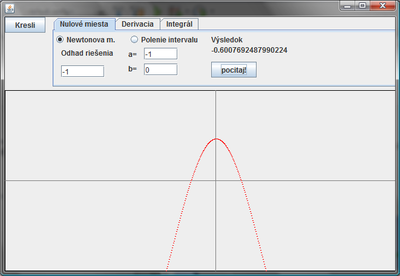
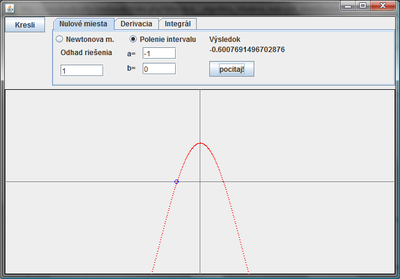
Na nasledujúcom obrázku je funkcia f(x)= 1*cos(2*x)-x^2, zobrazená na intervale <-5, 5>. Toto zodpovedá zápisu v konštrukture triede kiwikiApp (naša plikácia): 

    public kiwikiDemo_graf() {
        initComponents();
        f = new Function(1,2,2);
        t = new Transform(panel.getWidth(), panel.getHeight(), 5);
        s=new Solver(f,0.000001);
    }

Ukážka funkčnosti:

Aplikácia algoritmov hľadania nulových miest.


Vylepšenie funkcionality:

Do aplikácie doplníme vizuálne znázornenie riešenia. Nájdené riešenie znázorníme ako modrý krúžok.

Riešenie je jednoduché. Stačí doplniť vykreslenie kruhu na súradnice [x0,0], resp. v našom prípade [h1,0]. 

    private void tlcNulaActionPerformed(java.awt.event.ActionEvent evt) {
        double h1=0,h2 = 0;
        if(rbNewton.isSelected()){
            h1=Double.valueOf(textOdhadX.getText());
            h1=s.nulaNewton(h1);
        }
        if(rbPolenie.isSelected()){
            h1=Double.valueOf(textPolenieA.getText());
            h2=Double.valueOf(textPolenieB.getText());
            h1=s.nulaPolenie(h1, h2);
        }
        labelX0.setText(String.valueOf(h1));
        int r = 3;
        g.setColor(Color.blue);
        g.drawOval(t.getX(h1)-r, t.getY(0)-r, 2*r, 2*r);
    }
Aplikácia algoritmov hľadania nulových miest - znázornenie riešenia
Zdroj: „http://www.kiwiki.info/index.php?title=Java_-_algoritmy_hľadania_nulových_miest&oldid=9622“