Binárny strom

Z Kiwiki
Skočit na navigaci Skočit na vyhledávání
Imbox draft.png
 Toto je projekt, na ktorom sa ešte stále pracuje!!

Aj keď sú v tomto dokumente použiteľné informácie, ešte nie je dokončený. Svoje návrhy môžete vyjadriť v diskusii o tejto stránke.

Algoritmy a programovanie

Dátový typ

Štruktúry

Rekurzia

Algoritmy vyhľadávania

Algoritmy triedenia

Lineárny zoznam

Binárny strom

Numerické algoritmy

Grafové algoritmy

Strom je dynamická dátová štruktúra. Stromy sa používajú v prípade hierarchických vzťahov a rekurzívnych štruktúr objektov.

Practice.png
 Praktické príklady

Riešené príklady k tejto téme sú na stránke Binárny strom (riešené príklady)

Definícia

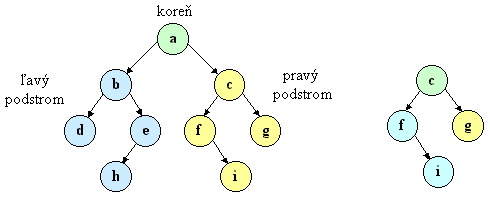
Binárny strom je v informatike stromová dátová štruktúra, ktorej každý vrchol má najviac dvoch potomkov. Zvyčajne sa označujú ako ľavý a pravý. Jedno z bežných použití binárneho stromu je binárny vyhľadávací strom; iné je binárna halda.

Strom má hierarchickú štruktúru: Rodič - potomok

Binárny strom je usporiadaný strom v ktorom má každý vrchol najviac dvoch synov.

Z programátorského hľadiska je výhodné údajovú štruktúru strom definovať pomocou rekurzie:

Strom typu T je buď [1]

  • prázdna množina alebo
  • vrchol typu T spolu s konečným počtom pripojených disjunktných stromov typu T, ktoré nazývame podstromy

Každý strom je tvorený ďalšími stromami, pre ktoré platí rovnaká definícia. Zviditeľníme ju na príklade binárneho stromu:

Príklad binárneho stromu

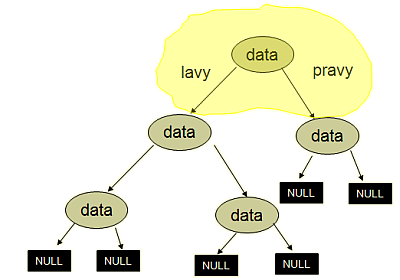
Na vedľajšom obrázku je vidieť, že aj podstrom sa skladá z koreňa a dvoch ďalších podstromov (niektorý z nich môže byť aj prázdny!). Každý list (t.j. vrchol bez synov) je tiež stromom, jeho ľavý aj pravý podstrom sú však prázdne.

Binárny vyhľadávací strom

Hodnoty v uzloch sú usporiadané tak, že pre každý uzol stromu u platí[2]:

  • hodnota uložená v u je väčšia alebo rovná ako hodnota uložená v ľavom podstrome u
  • hodnota uložená v u je menšia alebo rovná ako hodnota uložená v pravom podstrome u

Potom je možné v tomto strome jednoduchým spôsobom vyhľadať danú hodnotu h:

  1. nastav koreň ako aktuálny uzol (u)
  2. pokiaľ je v u uložená hodnota h, algoritmus končí (a vráti u)
  3. ak je u list, algoritmus končí (hodnota h nebola v strome nájdená)
  4. hodnota h sa porovná s hodnotou v u (nech je táto hodnota h')
    1. ak je [math]h \le h'[/math], do u sa uloží ľavý potomok u
    2. inak sa do u uloží pravý potomok u
  5. pokračuj bodom 2

Reprezentácia binárneho stromu

Štruktúra Tuzol binárneho stromu sa skladá z:

  • hodnoty (hodnôt) uzla
  • 2 ukazovateľov na ďalšie uzly (vetvy)
struct TUzol
{   int data;
    TUzol *lavy,*pravy;
};

V našom prípade je hodnota uzla premenná data, typu celé číslo. Premenná data môže byť ľubovoľného typu, napr. char, double, ale aj vlastne definovaných typov - štruktúra.

Usporiadanie prvkov TUzol v binárnom strome

Na sprístupnenie stromu potrebujeme ukazovateľ na koreň, v programe teda stačí deklarovať: 

TUzol *strom;

Ak niektorý vrchol nemá syna, hodnoty príslušných ukazovateľov sú NULL

Operácie s binárnym stromom

V nasledujúcich prípadoch budeme pracovať s binárnym vyhľadávacím stromom.

Vloženie hodnoty do stromu

Úloha: vložiť do stromu nový uzol. Nový uzol treba vložiť na správne miesto tak, aby bol strom usporiadaný.

Analýza:

  • Strom je prázdny. Novo vložený uzol bude koreňom stromu.
  • Strom nie je prázdny. V strome je už nejaký uzol. V tomto prípade treba zistiť, na ktorú stromu stromu sa má uzol vložiť.
    • Rozdhodnutie robíme podľa hodnoty dátovej časti nového uzla:
      • Ak je hodnota nového uzla menšia ako hodnota existujúceho uzla, tak ho dáme vľavo,
      • inak ho vložíme vpravo.
    • Ak je vpravo, alebo vľavo už nejaký uzol, postupujeme rekurzívne

Algoritmus vloženia:

Definujme procedúru Vloz, ktorá bude mať 2 parametre: Začiatočný uzol stromu, do ktorého budeme vkladať hodnotu. Keďže strom je rekurzívna štruktúra, algoritmus vloženia bude rekurzívny.

Procedúra Vloz( Uzol U, hodnota H)

  1. Ak aktuálny uzol U neobsahuje žiadnu hodnotu
    1. do dátovej časti uzla U nastav hodnotu H
    2. Nastav hodnoty smerníkov lavy a pravy uzla U na hodnotu NULL
    3. Koniec
  2. Ak je hodnota H < ako hodnota v uzle U
    1. Ak nemá uzol U ľavého potomka
      1. Vytvor nový uzol [math]U_n[/math] a nastav mu v dátovej časti prázdnu hodnotu
    2. Zavolaj procedúru Vloz s parametrami: Uzol U - ľavý (novo vytvorený) potomok uzla U ([math]U_n[/math]), hodnota - H
  3. Ak je hodnota H > ako hodnota v uzle U
    1. Ak nemá uzol U pravého potomka
      1. Vytvor nový uzol [math]U_n[/math] a nastav mu v dátovej časti prázdnu hodnotu
    2. Zavolaj procedúru Vloz s parametrami: Uzol U - pravý (novo vytvorený) potomok uzla U ([math]U_n[/math]), hodnota - H

Znázornenie algoritmu vloženia

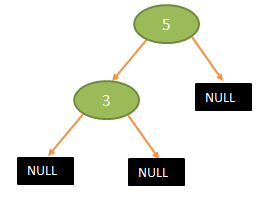
  • Počiatočný stav. Strom reprezentuje jeden vrchol, ktorý nemá hodnotu (v našom prípade ju znázorňuje hodnota 0)

  • Do stromu vkladáme hodnotu 5. V opísanom algoritme je táto situácia zachytená v kroku 1. Následne sa vykonajú kroky 1.1, 1.2 a 1.3

  • Do stromu vkladáme hodnotu 3. V algoritme platí krok 2. Krok 2.1 : uzol U nemá ľavého potomka tak takéhoto potomka vytvoríme (krok 2.1.1). Zavoláme procedúru Vloz s parametrami: uzol U - lavý potomok uzla U (teda novo vytvorený uzol). Po rekurzívnom zavolaní procedúry Vloz (krok 2.2) bude platiť podmienka v kroku 1.

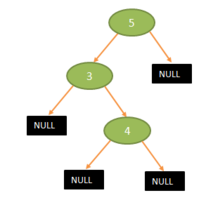
  • Do stromu vkladáme hodnotu 4. V algoritme platí krok 3. Krok 3.1 : uzol U nemá pravého potomka tak takéhoto potomka vytvoríme (krok 3.1.1). Zavoláme procedúru Vloz s parametrami: uzol U - pravý potomok uzla U (teda novo vytvorený uzol). Po rekurzívnom zavolaní procedúry Vloz (krok 3.2) bude platiť podmienka v kroku 2. Ďalší postup je rovnaký ako pri vkladaní hodnoty 3.

Prehľadávanie stromu

Za základnú operáciu sa však považuje prehľadávanie stromu (pohyb po strome). Vzhľadom na to, že strom je výhodne definovaný ako rekurzívna údajová štruktúra, aj na prehľadávanie sa využívajú rekurzívne metódy.

Keďže strom je rekurzívna štruktúra prehľadávanie stromu bude tiež rekurzívne. Podľa toho ako budeme postupovať pri prehľadávaní stromu, rozlišujeme metódy prehľadávania na:

  • preorder
  • inorder
  • postorder

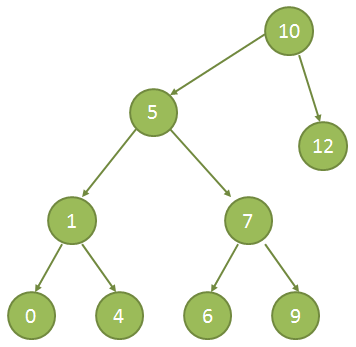
Majme nasledujúci binárny strom:

Usporiadaný binárny strom

Prehľadávanie preorder:

Postup prehľadávanie (výpisu hodnôt) binárneho stromu:

  • Vypíš hodnotu uzla
  • prehľadaj ľavý podstrom
  • prehľadaj pravý podstrom

Pri tomto postupe bude výpis binárneho stromu na predchádzajúcom obrázku nasledovný: 

10 5 1 0 4 7 6 9 12

Prehľadávanie inorder:

Postup prehľadávanie (výpisu hodnôt) binárneho stromu:

  • prehľadaj ľavý podstrom
  • Vypíš hodnotu uzla
  • prehľadaj pravý podstrom

Pomocou tohoto spôsobu prehľadávania stromu dostaneme pri výpise postupnosť usporiadaných hodnôt uzlov stromu od najmenšej po najväčšiu hodnotu. Pri tomto postupe bude výpis binárneho stromu na predchádzajúcom obrázku nasledovný: 

0 1 4 5 6 7 9 10 12

Prehľadávanie postorder:

Postup prehľadávanie (výpisu hodnôt) binárneho stromu:

  • prehľadaj ľavý podstrom
  • prehľadaj pravý podstrom
  • Vypíš hodnotu uzla

Pri tomto postupe bude výpis binárneho stromu na predchádzajúcom obrázku nasledovný: 

0 4 1 6 9 7 5 12 10

Zmazanie stromu

Princíp zmazania je podobný ako prechádzanie stromom:

  • Ak nemá uzol žiadneho potomka, zmažeme uzol
  • Ak má potomka
    • zmažeme ľavú časť stromu
    • Zmažeme pravú časť stromu

Implementácia v jazyku C

Vloženie hodnoty do stromu

void PridajUzol(TUzol *uzol, int udaj)
{
  if (!uzol-> data)  // ak v danom uzle nie su ziadne data- pridame novy udaj
  {   uzol->data = udaj;	// do uzla skopirujeme data
	uzol->lavy = uzol->pravy = NULL;  // nastavime pointre na lavy a pravy uzol
      return;
  }
  if(uzol->data >= udaj) // pridavame vlavo
  {  if (!uzol->lavy) // ak uzol vlavo neexisuje
     {  uzol->lavy = new TUzol; // tak ho vytvorime
	uzol->lavy->data=0;
     }
     PridajUzol(uzol->lavy, udaj); // opakujeme rekurzivne funkciu  s lavym uzlom
  }					
  else   // pridavame vpravo
  {  if (!uzol->pravy) 
     {   uzol-> pravy = new TUzol;
         uzol->pravy->data=0;
     }
     PridajUzol(uzol-> pravy, udaj);
  }
}

Výpis stromu inorder

void vypis(TUzol *s)
{    
   if(!s) 
      return;
   else    
   {  
      vypis(s->lavy);
      cout<<s->data<<endl;
      vypis(s->pravy);
   }
}

Vyhľadávanie v strome (inorder)

Funkcia hladaj bude v strome vyhľadávať uzol s hodnotou x. V prípade úspechu vráti smerník na tento prvok. V opačnom prípade vráti hodnotu NULL. 

TUzol* hladaj(TUzol *s, int x)
{    
   if(s==NULL) 
      return NULL;
   else    
   {  
      if(x < s->data)
         return hladaj(s->lavy,x); 
      if(s->data==x) 
         return s; 
      if(x > s->data)
        return hladaj(s->pravy,x);
   }
}

Zmazanie stromu

Princíp zmazania je podobný ako vypísania.

  • Ak nemá uzol žiadneho potomka, zmažeme aktuálny uzol
  • Ak má potomka
    • zmažeme ľavú časť stromu
    • zmažeme pravú časť stromu
void ZmazStrom(TUzol *uzol)
{
  if (!uzol) return;
  if (uzol->lavy)  // ak existuje lavy uzol
  {    ZmazStrom(uzol->lavy);
       delete uzol->lavy;
  }
  if (uzol->pravy) // ak existuje pravy uzol
  {    ZmazStrom(uzol->pravy);
       delete uzol->pravy;
  }
}

Zdroje

  1. ↑ http://cec.truni.sk/stoffov/dynamicke-udajove-struktury/Cast2/
  2. ↑ http://sk.wikipedia.org/wiki/Bin%C3%A1rny_vyh%C4%BEad%C3%A1vac%C3%AD_strom
Zdroj: „http://www.kiwiki.info/index.php?title=Binárny_strom&oldid=6656“