Obsah práce
1.	Teória hier
2.	Teória grafov
3.	Aplikácia stromov a princípov z teórie hier v niektorých ťahových hrách
4.	Implementácia algoritmov z teórie hier a teórie grafov do spoločenskej hry dáma

Úprava stránky Implementácia algoritmov z teórie hier a teórie grafov do spoločenskej hry dáma

Popis hry a jej reprezentácia v teórii hier

Dáma by sa v teórii hier dala charakterizovať ako nekooperatívna, symetrická, ťahová hra pre dvoch hráčov s nulovým súčtom a úplnými informáciami. Pravidlá tejto hry sú všeobecne známe, preto spomeniem len základné charakteristiky. Ide o hru dvoch hráčov na šachovnici 8x8, kde každý hráč má na začiatku osem figúrok na čiernych poliach v prvých dvoch radoch na protiľahlých stranách šachovnice. Pri rôznych verziách sa počty figúrok a veľkosť šachovnice líši (viď. ^[1]). Hráči sa snažia o odstránenie všetkých figúrok súpera ich preskakovaním. Vyhráva hráč, ktorý preskočí všetky figúrky súpera.

Najzrejmejšou formou interpretácie a analýzy tejto hry v teórii hier je teda rozšírená forma. V prípade, že by sme potrebovali analyzovať iba určité druhy problémových pozícií, dala by sa použiť aj normálna forma. No na reprezentáciu v rôznych fázach hry je táto forma nevhodná. Herný strom reprezentujúci hru dáma sa však s rastúcim počtom úrovní zväčšuje do takej miery, že je prakticky nemožné, aby človek analyzoval a hľadal správny ťah z takéhoto stromu. Takáto reprezentácia je ale vhodná pre počítačové spracovanie, kde je rozsiahlosť herného stromu vykompenzovaná rýchlosťou a presnosťou algoritmického riešenia počítačom. Ako zjavné riešenie sa teda ponúka minimaxová metóda. Cieľom riešenia je teda nájsť vhodný spôsob zapracovania tejto metódy do algoritmu vykonávaného počítačom.

Použitý jazyk a vývojové prostredie

Ako programovací jazyk som zvolil C++, s ktorým som už mal určité predošlé skúsenosti. Aj napriek občasnej ťažkopádnosti a komplikovanejším konštrukciám je tento jazyk veľmi často používaným hlavne pre svoju rýchlosť, množstvo dokumentácie a rozšírenosť.

Pri vývojovom prostredí padla voľba na C++ Builder vo verziách 2006 a 2010 od firmy Embarcadero Technologies, pretože s týmto editorom mám už dlhodobé skúsenosti a vyniká hlavne pomerne jednoduchou tvorbou užívateľského rozhrania vo Windows. Nevýhodou je nemožnosť kompilácie programu pre inú platformu, no táto požiadavka pre mňa nebola až tak podstatná.

Pre čítanie a zápis *.xml súborov som využil XML parser XML parser od autora Dr. F. V. Berghena, ktorý vyniká hlavne jednoduchosťou použitia a malou veľkosťou celej knižnice.

Základná štruktúra programovej implementácie

Obr. 15 – UML diagram tried

Pri vytváraní programu som sa sústredil predovšetkým na jednoduchosť a názornosť riešení jednotlivých problémov spojených s algoritmizáciou rôznych teoretických princípov a pravidiel. Taktiež som celý problém realizácie programu rozložil na viacero, funkčne čo najviac nezávislých celkov, ktoré sú jednoducho upraviteľné, prípadne plne nahraditeľné inými. Otázkou celkovej rýchlosti programu som sa veľmi nezaoberal, pretože som sa snažil hlavne o jasnú a zrozumiteľnú implementáciu. Taktiež by pri použití techník, zvyšujúcich rýchlosť algoritmov, nebolo možné natoľko oddeliť od seba jednotlivé časti programu a skomplikoval by sa aj popis činnosti jednotlivých funkčných blokov.

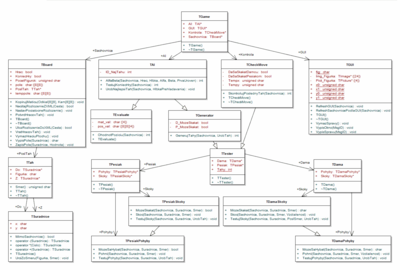
V mojej implementácii som celú hru rozložil na štyri základné časti reprezentované príslušnými objektovými triedami - šachovnica, kontrola ťahu, umelá inteligencia a užívateľské rozhranie.

Samotná šachovnica a základné operácie s ňou spojené sú tvorené triedou TBoard. Objekt vytvorený z tejto triedy je využívaný v celom programe a dal by sa prirovnať k reálnej šachovnici s figúrkami.

Ďalšou neoddeliteľnou súčasťou programu je kontrola správnosti hráčových ťahov reprezentovaná triedou TCheckMove. Objekt tejto triedy zamedzuje ľudskému hráčovi urobiť nelegálny ťah.

Jadrom „umelej inteligencie“ počítača, ktorá vyberá a vykonáva najvhodnejší ťah je trieda TAI. Bez príslušného objektu triedy TAI by celý program bol len elektronickou verziou dámy pre dvoch hráčov.

Pre samotné zobrazenie a ovládanie figúrok na šachovnici je v programe potrebný aj kód užívateľského rozhrania, ktorého najzákladnejšiu časť reprezentuje trieda TGUI. Táto trieda je len jedna z viacerých spojených s grafickým užívateľským rozhraním, no je najviac prepojená s ostatnými časťami programu.

Reprezentácia šachovnice

Obr. 16 – Súradnice prvkov matice reprezentujúcej šachovnicu

Obr. 17 – Hodnoty prvkov matice šachovnice na začiatku hry

Voľba vhodnej dátovej formy, ktorá bude v programe reprezentovať šachovnicu je veľmi dôležitá, pretože ovplyvňuje prakticky všetky algoritmy použité v ostatných častiach programu. Táto dátová štruktúra sa taktiež významnou mierou podieľa na celkovej rýchlosti aplikácie.

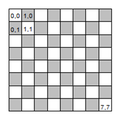
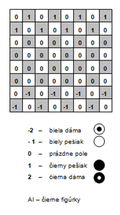
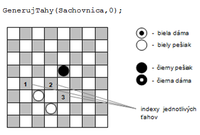
V mojom riešení som sa zameral hlavne na jednoduchý a pre mňa intuitívny spôsob reprezentácie šachovnice, preto som zvolil klasickú maticu 8x8, kde každý prvok matice odpovedá jednému políčku na šachovnici, pričom ľavé horné pole má súradnice 0,0. Každý prvok matice obsahuje celé číslo v rozsahu <-2,2>, ktoré reprezentuje figúrku v príslušnom poli šachovnice. Hodnota nula značí, že políčko šachovnice je prázdne.

Určitou nevýhodou tohoto riešenia je nutnosť samostatného testovania okrajov šachovnice, ktorá by sa eliminovala napr. použitím matice 10x10, kde prvky v okolí vnútornej matice 8x8 by mali určitú hodnotu symbolizujúcu okraj šachovnice a odpadla by nutnosť testovania súradníc. Takéto riešenie som však zavrhol kvôli prehľadnosti a názornosti s využitím matice 8x8.

V samotnom programe je matica šachovnice (char pole[8][8]) premennou, ktorá je súčasťou triedy TBoard. Okrem tejto matice obsahuje trieda TBoard aj ďalšie dôležité premenné a metódy využívané pri operáciách so šachovnicou. Objekt tejto triedy je potom predávaný ako parameter jednotlivým funkčným celkom programu.

Kontrola ťahov

Aby hráč nemohol vykonať ťah, ktorý by bol v rozpore s pravidlami hry, bolo nutné implementovať aj určitú formu kontroly správnosti hráčovho ťahu a vrátiť späť prípadný ilegálny ťah.

Obr. 18 – Hodnoty v premennej PoslTah pri vykonaní ťahu hráča

Samotnú kontrolu správnosti hráčovho posledného ťahu vykonáva metóda int SkontrolujPoslednyTah(TBoard Sachovnica) triedy TCheckMove. Objekt tejto triedy využíva premennú char temppole[8][8] a dátovú štruktúru TTah PoslTah z parametra Sachovnica, ktorý je objektom triedy TBoard.

Premenná temppole[8][8] triedy TBoard má úplne rovnaké vlastnosti ako pole[8][8] a využíva sa na dočasné uloženie rozloženia na šachovnici po hráčom vykonanom ťahu, aby bolo možné prípadne nesprávny ťah vrátiť o krok späť.

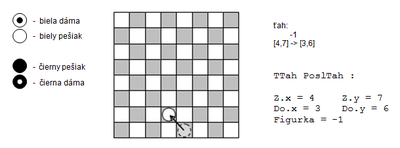
Dátový typ TTah, ktorý využíva premenná PoslTah je tvorený triedou, ktorá obsahuje dve premenné Z a Do typu TSuradnice a premennú reprezentujúcu figúrku, s ktorou hráč naposledy ťahal – char Figurka. Premenná Z obsahuje súradnice prvku matice šachovnice odkiaľ hráč ťahal. Premenná Do obsahuje zase súradnice, na ktoré sa hráč presunul.

Keďže algoritmický princíp kontroly možností pohybu a skákania figúrok je použiteľný aj v generátore ťahov, dedí trieda TCheckMove spolu s generátorom tieto testovacie metódy pohybu figúrok zo samostatnej triedy TTester.

Postup kontroly hráčovho ťahu je nasledovný:

Hráč v užívateľskom prostredí - GUI vykoná ťah, ktorý spôsobí zmenu rozloženia (pozície) na šachovnici.
Hráčov ťah sa uloží do premmenej PoslTah typu TTah. Zmena v GUI sa uloží do matice ukladajúcej dočasnú aktuálnu pozíciu – temppole[8][8].
Metóda SkontrolujPoslednyTah(TBoard Sachovnica) overí správnosť hráčovho ťahu.
Ak je hráčov ťah správny, tak táto funkcia vráti hodnotu 0 a pozícia uložená v temppole[8][8] sa prekopíruje do matice pole[8][8], ktorá reprezentuje aktuálne rozloženie na šachovnici.

V prípade, že je hráčov ťah nesprávny vráti kontrolná funkcia číslo, ktoré symbolizuje porušenie konkrétneho pravidla. Podľa tohoto čísla sa potom vypíše príslušné hlásenie o hráčovej chybe v ťahu. Rozloženie v GUI sa vráti do pôvodného stavu podľa matice pole[8][8].

Umelá inteligencia

Algoritmus výberu najvhodnejšieho ťahu je realizovaný na princípe metódy minimax s alfa-beta orezávaním. Pri použití tejto metódy je zrejmé, že okrem samotného vhodne upraveného minimax algoritmu sú potrebné ešte ďalšie dve súčasti. Prvou súčasťou je generátore ťahov, ktorý z každej danej pozície vie určiť a vykonať všetky možné ťahy. Ďalším nevyhnutným komponentom je funkcia na ohodnotenie pozície v listových vrcholoch herného stromu.

Pri tvorbe umelej inteligencie som teda využil tri komponenty:

generátor ťahov
ohodnocovacia funkcia
rozhodovacia funkcia (na princípe minimax metódy)

Prvé dve súčasti sú závislé od pravidiel konkrétnej hry, preto som ich do programu zapracoval ako samostatné a oddeliteľné celky.

Generátor ťahov

Obr. 19 – Volanie funkcie generátora ťahov s parametrom UrobTah = 0

Obr. 20 – Volanie funkcie generátora ťahov s parametrom UrobTah = 3

V minimax algoritme má generátor ťahov za úlohu vytvárať vrcholy herného stromu od koreňového (symbolizuje počiatočnú pozíciu) až po listové. Úlohou generátora je nájsť všetky možné legálne ťahy z aktuálne danej pozície a následne vykonať ťah, ktorý mu zadá algoritmus minimax.

Samotná realizácia generátora ťahov je veľmi špecifická vzhľadom na hru, ktorej ťahy sa generujú. Na ilustračnom príklade hry piškvorky v kapitole 3.1 je vidieť, že generátor ťahov má vlastne za úlohu iba nájsť voľné políčka, ktoré je možné obsadiť a samotný ťah je vykonaný iba obsadením prázdneho políčka symbolom krúžku alebo krížika. Generátor pre hru piškvorky je teda veľmi jednoduchý a ľahko programovo realizovateľný. Pri hre dáma je však situácia podstatne zložitejšia. Pravidlá pohybu jednotlivých figúrok sa programovo interpretujú oveľa komplikovanejšie, čo je spôsobené hlavne možnosťou viacnásobného skákania súperových figúrok a voľnejším pohybom dám, ktorý ešte viac komplikuje viacnásobné skákanie. To si vyžiadalo vytvorenie zložitejších funkcií, ktoré rekurzívne testujú rôzne možnosti viacnásobných skokov.

Generátor ťahov je teda jednou z najkomplikovanejších súčastí môjho programu a po hlbšej analýze som sa rozhodol nevyužiť samostatný generátor ťahov, ale generovať priamo pozície, ktoré by vznikli po vykonaní daného ťahu. Tým odpadá nutnosť tvorby samostatnej dátovej štruktúry pre uchovávanie vygenerovaných ťahov a funkcie, ktorá by dané ťahy realizovala nad danou pozíciou. Generátor ťahov v mojom programe tiež plní úlohu počítadla možných legálnych ťahov z aktuálnej pozície, ktoré je potrebné v algoritme minimax.

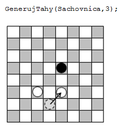
Obr. 21 – Grafické znázornenie triedy TTester

V programe je generátor ťahov realizovaný metódou int GenerujTahy(TBoard Sachovnica, int UrobTah) triedy TGenerator. Celá táto trieda je oddeliteľná a pri zmene alebo úprave triedy TBoard môže byť nahradená generátorom pre úplne odlišný typ hry. Musí sa však zachovať funkčnosť metódy GenerujTahy v závislosti od parametra UrobTah. Ak parameter UrobTah = 0, funkcia vráti počet možných legálnych ťahov z pozície danej v parametri Sachovnica. Pri UrobTah > 0 sa pozícia Sachovnica zmení vykonaním ťahu s indexom UrobTah. Pre bieleho hráča je princíp znázornený na obrázkoch Obr. 19 a Obr. 20.

Ako už bolo spomenuté v kapitole 4.5 o kontrole hráčových ťahov , tak trieda TGenerator dedí metódy testovania pohybu figúrok z triedy TTester. Zároveň však oproti triede TCheckMove (kontrola hráčových ťahov), využíva aj metódy, ktoré vykonajú daný ťah na zadanej pozícii.

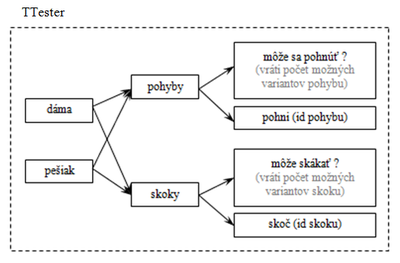
Trieda TTester pozostáva z komponentov uvedených na obrázku Obr. 21.

Ohodnocovanie pozícií

Ohodnotenie pozície z hľadiska konkrétneho hráča je v metóde minimax dôležité pri výbere vhodného ťahu v smere od ohodnotených listových vrcholov herného stromu až k počiatočnej pozícii v koreňovom vrchole. Funkcia ohodnocovania pozícií je pre výber vhodného ťahu v metóde minimax veľmi dôležitá a platí pravidlo, že čím presnejšie je daná pozícia ohodnotená, tým lepšia je potom umelá inteligencia celého programu. Rovnako ako v prípade generátora ťahov je aj funkcia ohodnocujúca jednotlivé pozície veľmi závislá od typu danej hry, preto som ju do programu implementoval ako samostatný celok nahraditeľný inou ohodnocovacou metódou. V mojom riešení som počítačového hráča (program) vybral za maximalizujúceho a ľudský hráč je minimalizujúci. To znamená, že všetky atribúty danej pozície výhodné pre počítačového hráča sú ohodnotené kladne a atribúty vhodné pre ľudského hráča záporne.

Keďže sám dámu nehrávam na vyššej úrovni, bolo by pre mňa pomerne obtiažne určovať presne hodnotu pozície z komplexnejšieho hľadiska. Preto som zvolil možnosť ohodnocovať len základné atribúty na danej pozícii a celý problém ohodnocovania pozícií som rozložil na dve časti:

materiálne ohodnotenie
pozičné ohodnotenie

O samotné ohodnotenie danej pozície sa stará metóda int OhodnotPoziciu(TBoard Sachovnica) triedy TEvaluate. Po zavolaní vráti funkcia celé číslo, ktoré symbolizuje hodnotu pozície v parametri Sachovnica. Táto trieda je taktiež nezávislá od ostatných častí programu a je nahraditeľná inou, ktorá bude pozície predávané parametrom Sachovnica, ohodnocovať iným spôsobom.

Jednotlivé materiálne a pozičné hodnoty sú definované v externom *.xml súbore. Editáciou tohoto súboru je umožnené vo veľkej miere nastaviť charakter hry výsledného programu a pri vhodných parametroch aj podstatne vylepšiť samotnú „umelú inteligenciu“.

Materiálne ohodnotenie

Táto forma ohodnotenia v podstate reprezentuje výhodnosť danej pozície z hľadiska počtu figúrok. Hra dáma je v tomto smere pomerne jednoducho charakterizovateľná, pretože vo väčšine prípadov platí, že čím väčší počet figúrok má hráč, tým je pre neho daná pozícia výhodnejšia. Je teda zrejmé, že figúrky ľudského – minimalizujúceho hráča (biela farba), budú všetky ohodnotené určitou zápornou hodnotou a všetky figúrky počítačového protivníka (čierna farba), ktorý maximalizuje, naopak budú ohodnotené kladne. Ak stanovíme, že každá figúrka bude mať absolútnu materiálnu hodnotu 1. Potom v určitom konkrétnom príklade, kde na šachovnici bude 5 bielych figúrok a 3 čierne figúrky, bude celková hodnota danej pozície -2, čo znamená, že pozícia bude výhodná pre minimalizujúceho hráča.

V hre dáma sa však vyskytujú dva rôzne typy figúrok – pešiaci a dámy. To vytvára problém určenia vzájomného optimálneho pomeru hodnôt medzi týmito dvoma typmi hracích figúrok. Z poznania pravidiel hry je však na prvý pohľad zrejmé, že hodnota figúrky dámy by mala byť vyššia ako hodnota pešiaka. V mojej implementácii som sa rozhodol, že dáma bude mať viac ako trojnásobnú hodnotu pešiaka. Tým by sa malo zabezpečiť dostatočné preferovanie pozícií v hernom strome, ktoré vedú k vytvoreniu dámy.

Zápis materiálnych hodnôt v *.xml súbore je nasledovný:

<?xml version="1.0" encoding="utf-8"?>
<hodnoty>
   <materialne>   <!—-materiálne ohodnotenie-->
      <!—-ohodnotenie figúrok ľudského hráča (minimalizuje)-->
      <hrac p_val="-3" d_val="-10"/>
      <!—-ohodnotenie figúrok umelej inteligencie (maximalizuje)-->
      <ai p_val="3 " d_val="10"/>
      </materialne>
   <pozicne>
      <!—-pozičné ohodnotenie-->		
   </pozicne>
</hodnoty>

Materiálne ohodnotenie je tvorené elementom materialne. Atribút p_val elementu hrac určuje hodnotu pešiaka ľudského hráča a atribút d_val hodnotu dámy. Materiálne ohodnotenie počítačového hráča v elemente ai je ekvivalentné.

Pri určovaní konkrétnej materiálnej hodnoty jednotlivých figúrok je však dôležité aj pozičné ohodnotenie a to opäť hlavne nájdenie správneho pomeru medzi ohodnotením výhodnej pozície a materiálnym ohodnotením figúrky.

Pozičné ohodnotenie

Tento spôsob ohodnocovania je založený na znalosti určitých strategicky výhodných a nevýhodných pozícií. V zjednodušenej forme ide o obsadenie políčok šachovnice, ktoré majú výhodnú polohu a výhybanie sa poliam s nevhodnou polohou. V dáme sú za výhodné políčka považované zadné rady šachovnice oboch hráčov, ktoré, ak sú obsadené, tak protihráčovi znemožňujú vytvorenie figúrky dámy. Taktiež je výhodné obsadiť krajné polia na pravej a ľavej strane, ktoré zase znemožňujú protihráčovi preskočiť figúrky na týchto políčkach. Ďalšími možnými strategicky výhodnými polohami som sa nezaoberal, no je možné ich doplniť do *.xml súboru s jednotlivými ohodnoteniami.

Štruktúra zápisu pozičného ohodnotenia v *.xml súbore je nasledovná:

<?xml version="1.0" encoding="utf-8"?>
<hodnoty>
   <materialne>
      <!—-materiálne ohodnotenie--> 
   </materialne>
   <pozicne>	<!—-pozičné ohodnotenie-->
      <pos_val x="0" y="7" fig_val="-1" hodnota="-1"/>						 

      <!—-tu sa nachádzajú ďalšie elementy pos_val-->
			
   </pozicne>
</hodnoty>

Celé pozičné ohodnotenie je tvorené elementom pozicne, ktorý obsahuje elementy pos_val reprezentujúce jednotlivé strategicky výhodné (nevýhodné) polia šachovnice. Elementov pos_val môže byť ľubovoľný počet a každý z nich obsahuje atribúty x a y, ktoré určujú súradnice výhodného (nevýhodného) poľa na šachovnici, atribút fig_val určujúci pre akú figúrku je dané pole výhodné (nevýhodné) a posledným atribútom je hodnota, ktorý udáva číselné ohodnotenie, v prípade, že daná figúrka obsadí konkrétne pole.

V uvedenom elemente pos_val je zadané, že ak je pole so súradnicami [0,7] obsadené figúrkou reprezentovanou číslom -1 (biely pešiak), tak sa celková hodnota pozície zníži o -1, čo je pre bieleho hráča výhodné, pretože minimalizuje. Ak by atribút hodnota bol rovný 1, potom by pre bieleho hráča bola daná pozícia nevýhodná.

Rozhodovacia funkcia

Ako už bolo spomenuté, pri tvorbe a prehľadávaní herného stromu v mojej implementácii je využitý algoritmus minimax. Tento však sám o sebe nehovorí nič o optimálnom ťahu, ktorý by sa mal vykonať. Výstupom tohto algoritmu je iba číselná hodnota najlepšej pozície pre daného hráča, ktorú je možné dosiahnuť z aktuálnej (koreňovej) pozície, a to za predpokladu, že obaja hráči vykonajú vždy najoptimálnejší ťah. Ak by algoritmus minimax mohol vytvoriť a preskúmať celý herný strom až do všetkých možných koncov hry (listové vrcholy) a jeho výstupom by bola nula, potom by to znamenalo, že pri neomylnosti oboch hráčov nie je možné hru ukončiť inak ako remízou.

Z hľadiska voľby vhodného ťahu z danej pozície je však výstup samotného minimax algoritmu pomerne nepoužiteľný. Preto bolo aj v mojej implementácii potrebné vhodne tento algoritmus upraviť tak, aby bolo možné rozhnodnúť, ktorý ťah je najlepšie vykonať z danej pozície.

V mojom riešení sa o výber vhodného ťahu starajú metódy int AlfaBeta(...) a UrobNajlepsiTah(TBoard Sachovnica,unsigned int HlbkaPrehladavania) triedy TAI. V ďalšom popise sa budem najskôr venovať samotnej programovej implementácii metódy minimax. Spôsob výberu optimálneho ťahu za pomoci tejto metódy bude opísaný až v kapitole 4.9.3.

Implementácia algoritmu minimax

Už z popisu princípu algoritmu minimax je zrejmé, že hlavná činnosť, ktorú algoritmus vykonáva pozostáva z dvoch fáz. Prvou fázou je generovanie jednotlivých vrcholov herného stromu, ktoré reprezentujú pozície konkrétnej hry. To sa deje pomocou generátora ťahov až pokiaľ sa nenarazí na listový vrchol. Listové vrcholy sú tvorené zväčša vrcholmi, ktoré sa nachádzajú v zadanej hĺbke herného stromu, no môžu ich tvoriť aj koncové pozície hry. Všetky listové vrcholy sú potom ohodnotené ohodnocovacou funkciou. Potom sa v algoritme už ďalšie ťahy negenerujú ale nastúpi druhá fáza minimaxového algoritmu, ktorá prebieha smerom “hore“ z listových vrcholov a z ohodnotených vrcholov vyberá najmenšiu alebo najväčšiu hodnotu, ktorou ohodnotí vrchol o stupeň vyššie. Takto pokračuje až ku koreňovému vrcholu a v momente, kedy sa vyberie hodnota pre koreňový vrchol sa algoritmus zastaví.

Základnú činnosť minimax algoritmu pre vykonanie všetkých možných ťahov z danej pozície, následné ohodnotenie zmenených pozícií a vybratie najväčšej hodnoty z nich je možné popísať pseudokódom podobným jazyku C.

jednourovnovyminimax(Pozicia) 
{                
   NajlepsiaHodnota=-∞;
   //zisti sa pocet moznych tahov z danej pozicie
   pocet=ZistiPocetMoznychTahov(Pozicia);     
   //postupne sa vykonavaju mozne tahy
   for(IndexTahu=1, IndexTahu<pocet, IndexTahu++) 
   {
      UrobTah(Pozicia, IndexTahu);   
      //kazdy tah sa ohodnoti
      Hodnota=OhodnotPoziciu(Pozicia); 
      //pozicia sa po vykonani a ohodnoteni tahu vrati do //pociatocneho stavu
      VratTah(Pozicia, IndexTahu);
      //tu sa vybera najvyssia hodnota z hodnot vsetkych tahov v //danej urovni
      if(Hodnota>NajlepsiaHodnota)
         NajlepsiaHodnota=Hodnota;
   } 	
   //funkcia vrati najvyssiu hodnotu
   return NajlepsiaHodnota;
}

Z daného kódu je zrejmé, že v tomto tvare algoritmus skúma ťahy len do hĺbky 1. To znamená, že vráti najväčšiu hodnotu ťahu, ktorý môže byť urobený z danej koreňovej pozície, ale do ohodnotenia ťahov sa nepremieta ďalší možný vývoj hry. Tiež je vidieť, že funkcia je upravená iba pre maximalizujúceho hráča, pretože sa hľadá, čo najvyššia hodnota pozície.

Aby bolo možné preskúmať ťahy až do určitej hĺbky, prípadne do miesta, kde hra končí, je treba túto minimaxovú funkciu upraviť do rekurzívnej podoby. Tú znázorňuje nasledujúcí pseudokód.

negamax(Pozicia, HlbkaPrehladavania) 
{                
   NajlepsiaHodnota=-∞;
   //ak sa dospeje do vopred danej hlbky alebo je aktualna pozicia //koncova, tak sa pozicia ohodnoti
   if(HlbkaPrehladavania<=0 || KoncovaPozicia(Pozicia)==TRUE)
      return OhodnotPoziciu(Pozicia); //staticka hodnota pozicie
   pocet=ZistiPocetMoznychTahov(Pozicia);  
   for(IndexTahu=1, IndexTahu<pocet, IndexTahu++) 
   {
      UrobTah(Pozicia, IndexTahu);   
      //tu funkcia zavola samu seba a znova generuje nove 
      //pozicie pre aktualnu poziciu
      Hodnota=-negamax(Pozicia, HlbkaPrehladavania-1);
      VratTah(Pozicia, IndexTahu);
      if(Hodnota>NajlepsiaHodnota)
         NajlepsiaHodnota=Hodnota;
   } 	
   return NajlepsiaHodnota;
}

Za pozornosť tu stojí znamienko mínus pri rekurzívnom volaní funkcie. To znamená, že vrátená hodnota pozície sa po každom rekurzívnom volaní prevráti na opačnú hodnotu. To je dôležité z toho dôvodu, že na ťahu je striedavo maximalizujúci a minimalizujúci hráč. Takýmto spôsobom potom netreba hľadať raz maximálnu a raz minimálnu hodnotu, ale stále len maximálnu. Túto metódu ilustruje nasledujúci príklad:

A = {-1,4,-8,2} , max(A) = 4 , min(A) = -8 ==> min(A) == -max(-A)

Ďalej je dôležité, aby funkcia OhodnotPoziciu(Pozicia) vracala tzv. statickú hodnotu pozície. Je to taká hodnota, ktorá je kladná, ak je aktuálny hráč vo výhode a záporná ak je v nevýhode. A to bez ohľadu na to, ktorý z hráčov maximalizuje alebo minimalizuje. Celá táto úprava minimaxového algoritmu je známa pod názvom negamax.

Alfa-beta orezávanie

Z praktického hľadiska je problém výberu optimálneho ťahu v programe vyriešený už funkciou negamax. No v dáme je často možné vykonať veľké množstvo rôznych ťahov, ktoré podstatne rozširujú herný strom, ktorý musí minimax algoritmus prejsť, čo sa negatívne prejaví na čase spracovania stromu. Výraznú úsporu počtu vetiev, ktoré treba preskúmať však predstavuje použitie metódy alfa-beta orezávania. Táto metóda má aj tú výhodu, že dáva rovnaké výsledky ako samotný algoritmus minimax. Jej implementácia do existujúcej minimaxovej funkcie je navyše pomerne jednoduchá ako ukazuje pseudokód na ďalšej strane:

alfabeta(Pozicia, HlbkaPrehladavania, alfa, beta) 
{                
   NajlepsiaHodnota=-∞;
   if(HlbkaPrehladavania<=0 || KoncovaPozicia(Pozicia)==TRUE)
      return OhodnotPoziciu(Pozicia);
   pocet=ZistiPocetMoznychTahov(Pozicia);  
   for(IndexTahu=1, IndexTahu<pocet, IndexTahu++) 
   {
      UrobTah(Pozicia, IndexTahu);   
      //hodnoty alfa a beta sa musia “prevratit” pre druheho hraca
      Hodnota=-minimax(Pozicia, HlbkaPrehladavania-1, -beta, -alfa);
      VratTah(Pozicia, IndexTahu);
      if(Hodnota>NajlepsiaHodnota)
         NajlepsiaHodnota=Hodnota;
      //ak sa najde nevyhodna hodnota pre maximalizujuceho hraca, tak 
      //sa z danej nevyhodnej vetvy hned ”vyskoci” a usetri sa cas
      if(NajlepsiaHodnota>=beta)  
         break; //vyskocenie z for cyklu
      if(NajlepsiaHodnota>alfa)
         alfa=NajlepsiaHodnota; 
   } 
   return NajlepsiaHodnota; 
}

Prvotné zavolanie funkcie musí mať potom nasledujúci tvar:

alfabeta(Pozicia, HlbkaPrehladavania, -∞, ∞);

Funkcia algoritmu minimax s alfa-beta orezávaním je v programe implementovaná metódou int AlfaBeta(TBoard Sachovnica,bool Hrac,unsigned int Hlbka,int Alfa,int Beta,bool PrvaUroven) triedy TAI. Táto metóda vracia hodnotu optimálneho ťahu. Parameter Sachovnica udáva aktuálnu pozíciu. Hrac je parameter striedavo nadobúdajúci hodnotu TRUE alebo FALSE (pravda/nepravda) v jednotlivých rekurzívnych volaniach a symbolizuje hráča, ktorý je v hernom strome aktuálne na ťahu. Táto informácia je dôležitá pri zisťovaní statickej hodnoty pozície. Ďalším parametrom je hĺbka prehľadávania - Hlbka, ktorá určuje počet úrovní výsledného herného stromu. Nasledujú parametre Alfa a Beta, ktoré určujú hranice prehľadávaných hodnôt v strome. Posledný parameter PrvaUroven je pomocnou premennou pre samotný výber optimálneho ťahu, ktorý je popísaný v nasledujúcej kapitole.

Výber najlepšieho ťahu

Na to, aby bolo možné zistiť, aký ťah je najvhodnejšie urobiť z aktuálnej danej pozície, ktorá je analyzovaná minimax metódou, som sa rozhodol upraviť samotnú minimax funkciu tak, aby si vedela zapamäť index najlepšieho ťahu z počiatočnej pozície, teda z koreňového vrcholu herného stromu. Na zistenie, či sa jedná o ťahy z počiatočnej pozície je využitý parameter bool PrvaUroven, ktorý musí mať pri prvotnom zavolaní funkcie hodnotu TRUE. Hodnota tohto parametra pri ďalších rekurzívnych volaniach funkcie AlfaBeta(...) je FALSE. Takto funkcia vie, že má určovať index najlepšieho ťahu, iba v prvej úrovni herného stromu. Výsledný pseudokód alfa-beta funkcie je nasledovný:

alfabeta(Sachovnica, Hrac, Hlbka, Alfa, Beta, PrvaUroven) 
{                
   NajlepsiaHodnota=-∞;

   if(Hlbka<=0 || KoncovaPozicia(Sachovnica)==TRUE)
      if(Hrac) 
         //ludsky hrac minimalizuje, preto sa jeho ohodnotenie
         //musi prevratit, aby hodnota pozicie bola staticka
         return -OhodnotPoziciu(Pom_Sach); 
      else
         return OhodnotPoziciu(Pom_Sach);
   pocet=ZistiPocetMoznychTahov(Sachovnica);  
   for(IndexTahu=1, IndexTahu<pocet, IndexTahu++) 
   {
      UrobTah(Sachovnica, IndexTahu);   
      Hodnota=-minimax(Pozicia,otoc(Hrac),Hlbka-1,-Beta,-Alfa,FALSE);
      VratTah(Sachovnica, IndexTahu);
	    	
      if(Hodnota>NajlepsiaHodnota)
      {
         NajlepsiaHodnota=Hodnota;
         //ak sa vykonavaju jednotlive tahy z pociatocnej pozicie, 
         //tak sa ulozi index najlepsieho tahu
         if(PrvaUroven==TRUE)
            IndexNajTahu=i;	
      }
      if(NajlepsiaHodnota>=Beta)  
         break;  
      if(NajlepsiaHodnota>Alfa)
         Alfa=NajlepsiaHodnota; 
   } 
   return NajlepsiaHodnota; 
}

Ako už bolo spomenuté, parameter Hrac nadobúda hodnoty TRUE alebo FALSE, kde TRUE znamená, že je v hernom strome na ťahu ľudský hráč a FALSE symbolizuje ťahanie počítačového protivníka. Prvotné zavolanie tejto funkcie preto pre výpočet ťahu umelej inteligencie musí mať tvar:

alfabeta(Sachovnica, FALSE, Hlbka, -∞, ∞, TRUE)

Ľudský hráč (biely) minimalizuje a tým pádom je vo výhode, ak majú pozície záporné ohodnotenie. Pre statickú hodnotu však treba túto hodnotu obrátiť, aby výhodná pozícia bola mala hodnotu kladnú.

Z takejto funkcie už vieme index ťahu, ktorý je z danej pozície najlepšie vykonať. Keďže mnou implementovaný generátor ťahov vie aj priamo vykonávať ťahy podľa zadaného indexu, je už realizácia samotného optimálneho ťahu jednoduchá. Celé vykonanie najlepšieho ťahu má na starosti metóda UrobNajlepsiTah(TBoard Sachovnica,unsigned int HlbkaPrehladavania) triedy TAI. Táto metóda zavolá alfa-beta funkciu so správnymi parametrami a potom pomocou generátora ťahov vykoná ťah s indexom IndexNajTahu.

Úroveň umelej inteligencie je pomerne dobrá aj vzhľadom na amatérsky spôsob ohodnocovania jednotlivých pozícií. Na úspešnosť ťahov samotného algoritmu má samozrejme vplyv aj nastavená hĺbka prehľadávania v algoritme minimax. Už pri hĺbke 5 je hra pre bežného hráča pomerne obtiažna. Pričom je možné nastaviť maximálne hĺbku prehľadávania 10. Väčšia úroveň prehľadávania sa negatívne podpíše na celkovej rýchlosti programu.

Grafické užívateľské rozhranie

Obr. 22 – Okno aplikácie

Prepojenie s jadrom programu

O zobrazenie a ovládanie priebehu hry užívateľom programu sa stará viacero rôznych funkcií, ktoré však už nie sú natoľko podstatné pre samotné jadro programu. Tieto funkcie sú taktiež veľmi výrazne späté s použitým vývojovým prostredím. Pretože som však chcel výraznejšie oddeliť jadro programu a samotné grafické rozhranie, rozhodol som sa pre vytvorenie štruktúry, ktorá by slúžila ako prepojenie medzi týmito dvoma funkčnými celkami.

Týmto spojovacím článkom je trieda TGUI, ktorá obsahuje dve hlavné metódy realizujúce spojenie s jadrom programu. Metóda RefreshGUI(TBoard Sachovnica) obnoví rozloženie figúrok na šachovnici v grafickom rozhraní podľa matice šachovnice v triede TBoard. Ďalšia metóda RefreshSachovnicePodlaGUI(TBoard Sachovnica) naopak zapíše do matice šachovnice hodnoty z grafického rozhrania. Zvyšné metódy triedy TGUI sa starajú o výpis potrebných správ a okien s hláseniami.

Popis rozhrania aplikácie

Celé užívateľské prostredie programu je vytvorené priamo v prostredí editoru C++ Builder a je tvorené jedným oknom, ktoré obsahuje všetky nutné ovládacie prvky. Keďže mojim cieľom bola hlavne praktická implementácia teoretických postupov, je program tvorený iba najzákladnejšími funkčnými celkami nutnými k realizácii.

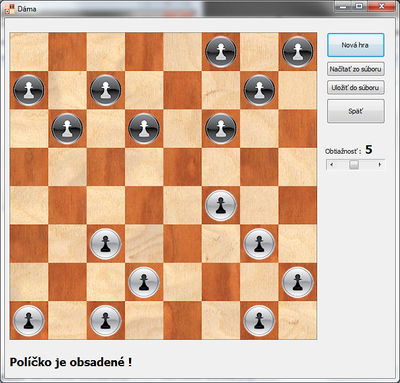
Najdôležitejšou súčasťou grafického užívateľského prostredia je samotná šachovnica s figúrkami. Obrázky šachovnice a jednotlivých figúrok sú načítavané z *.bmp súborov. Napravo od šachovnice sú tlačidlá na spustenie novej hry, načítanie a uloženie pozície a na vrátenie ťahu o jeden krok späť. Pod šachovnicou sa nachádza priestor pre zobrazenie správ o nelegálnom ťahu užívateľa.

Ovládanie

Presun jednotlivých figúrok na šachovnici je realizovaný myšou. Po umiestnení kurzora nad obrázok figúrky a následným stlačením ľavého tlačidla myši užívateľ „uchopí“ požadovanú figúrku. Pohybom myši pri stlačenom ľavom tlačidle sa potom dá figúrka „ťahaním“ premiesťnovať na šachovnici. Program sám zabezpečuje, že figúrkou nie je možné ťahať na biele polia šachovnice. Pri ilegálnom ťahu sa figúrka vráti na pôvodnú polohu a v spodnej časti okna sa vypíše hlásenie o chybe v hráčovom ťahu. Po správnom ťahu užívateľa je ihneď vykonaný ťah počítača a opäť je na ťahu užívateľ. Pri možnosti viacnásobného skákania sa otvorí dialógové okno s otázkou, či chce užívateľ ďalej skákať.

V pravej časti okna programu je možné tlačidlom spustiť novú hru, prípadne uložiť alebo načítať zo súboru rozloženie figúrok na šachovnici. Pritom sa zobrazí dialógové okno na výber *.xml súboru s uloženou alebo práve ukladanou pozíciou. Ďalej program umožňuje vrátiť ťah o jeden krok späť. Keďže v aplikácii nie je zabudovaná funkcia prehrávania jednotlivých ťahov, je možné posunúť sa z každej pozície naspäť iba o jeden ťah.

Posledným ovládacím prvkom je posuvník na nastavenie obtiažnosti. Hodnota nastavenej obtiažnosti priamo zodpovedá hĺbke prehľadávania ťahov v metóde minimax. To znamená, že čím väčšia je nastavená hĺbka prehľadávania, tým je lepšia úroveň umelej inteligencie.

Po ukončení hry sa otvorí dialógové okno so správou o výhre, prehre alebo remíze a začne sa nová hra.

Záver

Cieľom práce bolo objasniť základy teórie hier a teórie grafov a tieto poznatky potom aplikovať do programu v praktickej časti. V teoretickej časti sú popísané spôsoby reprezentácie rozhodovacích problémov a samostatná časť je venovaná ich riešeniu a to hlavne hľadanie optimálnej stratégie v hrách reprezentovaných hernými stromami.

Praktická časť je venovaná tvorbe aplikácie, ktorá by využívala umelú inteligenciu v doskovej hre dáma. Celá umelá inteligencia je založená na algoritme minimax, rozšírenom o metódu alfa-beta orezávania.

Pomerne netradične je v mojej implementácii poňatý generátor ťahov, ktorý priamo generuje jednotlivé pozície. Tento postup sa ukázal ako vhodný a napomohol k zjednodušeniu a sprehľadneniu výsledného programu.

Výsledná programová implementácia je pomerne úspešná a pre neprofesionálneho hráča je hra dostatočne obtiažna.

Program je možné ďalej v budúcnosti doplniť o pokročilejšie metódy zrýchľujúce minimax algoritmus a spresniť ohodnocovanie pozícií. Taktiež sa ponúka možnosť výsledný kód prepísať do multiplatformovej podoby, prípadne vytvoriť online verziu programu s využitím rôznych webových technológií.

Spustiteľná verzia programu

Spustiteľná verzia programu hry dáma je dostupná TU.

Zoznam použitej literatúry

Game theory. Wikipedia. [Online] 2009. [Dátum: 2. 1 2009.] http://en.wikipedia.org/wiki/Game_theory.
Nash equilibrium. Wikipedia. [Online] 2008. [Dátum: 2. 1 2009.] http://en.wikipedia.org/wiki/Nash_equilibrium.
Kadlic, Michal. Iterovaná väzňova dilema. [Online] 2008. [Dátum: 2. 1 2009.] http://www2.fiit.stuba.sk/~kapustik/ZS/Clanky0405/kadlic/ipd.html.
RAND. Wikipedia. [Online] 2008. [Dátum: 2. 1 2009.] http://en.wikipedia.org/wiki/RAND.
Nečas, Jiří. Grafy a jejich použití. Praha : SNTL, 1978.
Plesník, Ján. Grafové algoritmy. Bratislava : VEDA, 1983.
Graph coloring. Wikipedia. [Online] 2008. [Dátum: 2. 1 2009.] http://en.wikipedia.org/wiki/Graph_coloring.
Flow network. Wikipedia. [Online] 2009. [Dátum: 2. 1 2009.] http://en.wikipedia.org/wiki/Network_flow.
Wróblewski, Piotr. Algoritmy, datové struktury a programovací techniky. Brno : Computer Press, 2004.
Game tree. Wikipedia. [Online] 2008. [Dátum: 25. 11 2008.] http://en.wikipedia.org/wiki/Game_tree.
Dáma (hra). Wikipedia. [Online] 2010. [Dátum: 7. 4 2010.] http://sk.wikipedia.org/wiki/D%C3%A1ma_(hra).
Berghen, Frank Vanden. C++ XML Parser. Kranf Site. [Online] [Dátum: 5. 2 2010.] http://www.applied-mathematics.net/tools/xmlParser.html.
Teória hier. Wikipedia. [Online] 2008. [Dátum: 2. 1 2009.] http://sk.wikipedia.org/wiki/Te%C3%B3ria_hier.
Zachar, Peter. Teória hier : história matematiky. [Online] 2008. [Dátum: 2. 1 2009.] http://fedu.ku.sk/~tkacik/predmety/download/hm/prace/zachar.pdf.
Extensive-form game. Wikipedia. [Online] 2008. [Dátum: 2. 1 2009.] http://en.wikipedia.org/wiki/Extensive_form_game.
Normal-form game. Wikipedia. [Online] 2008. [Dátum: 2. 1 2009.] http://en.wikipedia.org/wiki/Normal_form_game.
Graph theory. Wikipedia. [Online] 2008. [Dátum: 2. 1 2009.] http://en.wikipedia.org/wiki/Graph_theory.
Glossary of graph theory. Wikipedia. [Online] 2008. [Dátum: 2. 1 2009.] http://en.wikipedia.org/wiki/Glossary_of_graph_theory.
Graph (mathematics). Wikipedia. [Online] 2008. [Dátum: 2. 1 2009.] http://en.wikipedia.org/wiki/Graph_(mathematics).
Podgraf. Wikipedia. [Online] 2008. [Dátum: 2. 1 2009.] http://sk.wikipedia.org/wiki/Podgraf.
Kružnica (graf). Wikipedia. [Online] 2008. [Dátum: 2. 1 2009.] http://sk.wikipedia.org/wiki/Kru%C5%BEnica_(graf).
Decision tree. Wikipedia. [Online] 2008. [Dátum: 11. 25 2008.] http://en.wikipedia.org/wiki/Decision_tree.
Seven Bridges of Königsberg. Wikipedia. [Online] 2008. [Dátum: 2. 1 2009.] http://en.wikipedia.org/wiki/Seven_Bridges_of_K%C3%B6nigsberg.
Game complexity. Wikipedia. [Online] 2008. [Dátum: 25. 11 2008.] http://en.wikipedia.org/wiki/Game-tree_complexity.
Dobeš, Dušan. Minimax a Alphabeta: cesta do srdce šachových programů. Computerworld. [Online] 1999. [Dátum: 2. 1 2009.]http://archiv.computerworld.cz/cwarchiv.nsf/clanky/1DDC3C7432078B37C12569B00054536A?OpenDocument.
Minimax. Wikipedia. [Online] 2008. [Dátum: 25. 11 2008.] http://en.wikipedia.org/wiki/Minimax.
Alpha-beta pruning. Wikipedia. [Online] 2008. [Dátum: 25. 11 2008.] http://en.wikipedia.org/wiki/Alpha-beta_pruning.
Bodén, Mikael. Alpha-beta pruning example. emunix.emich.edu. [Online] 2006. [Dátum: 25. 11 2008.] http://www.emunix.emich.edu/~evett/AI/AlphaBeta_movie/sld018.htm.
Draughts. Wikipedia. [Online] 2009. [Dátum: 2. 1 2009.] http://en.wikipedia.org/wiki/Draughts.
Nešetřil, Jaroslav. Teorie grafů. Praha : SNTL, 1979. s. 316. 04-017-79.
Kadlec, Václav. Učíme se programovat v jazyce C. Brno : CP Books, 2005.
Kadlec, Václav. Učíme se programovat v Borland C++ Builder a jazyce C++. Brno : Computer Press, 2004.

Odkazy

↑ Dáma (hra). Wikipedia. [Online] 2010. [Dátum: 7. 4 2010.] http://sk.wikipedia.org/wiki/D%C3%A1ma_(hra).

[dama_hra-1] Dáma (hra). Wikipedia. [Online] 2010. [Dátum: 7. 4 2010.] http://sk.wikipedia.org/wiki/D%C3%A1ma_(hra).

[1]

Implementácia algoritmov z teórie hier a teórie grafov do spoločenskej hry dáma

Obsah

Úprava stránky Implementácia algoritmov z teórie hier a teórie grafov do spoločenskej hry dáma

Popis hry a jej reprezentácia v teórii hier

Použitý jazyk a vývojové prostredie

Základná štruktúra programovej implementácie

Reprezentácia šachovnice

Kontrola ťahov

Umelá inteligencia

Generátor ťahov

Ohodnocovanie pozícií

Materiálne ohodnotenie

Pozičné ohodnotenie

Rozhodovacia funkcia

Implementácia algoritmu minimax

Alfa-beta orezávanie

Výber najlepšieho ťahu

Grafické užívateľské rozhranie

Prepojenie s jadrom programu

Popis rozhrania aplikácie

Ovládanie

Záver

Spustiteľná verzia programu

Zoznam použitej literatúry

Odkazy

Navigačné menu

Osobné nástroje

Menné priestory

Varianty

Zobrazenia

Viac

Hľadať

Navigácia

Rýchle linky

Nástroje