Riešenie obvodov metódou slučkových prúdov
Maticové metódy rozširujúceho balíka Pythonu pylab[1] je možné použiť pre analýzu jednoduchej elektrickej siete metódou slučkových prúdov.
Analýza obvodu
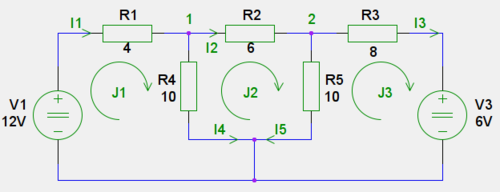
Analyzovaný obvod pozostáva z rezistorov a napäťových zdrojov. V obvode sú vyznačené slučkové prúdy J1, J2 a J3.
Pre slučku J1 môžeme na základe druhého Kirchhofovho zákona písať
- [math] R1 J1 + R4 (J1-J2)=V1 \, [/math]
pre slučku J2
- [math] R2 J2 + R5 (J2-J3) + R4(J2-J1) = 0 \, [/math]
a pre slučku J3
- [math] -R5 J2 + (R3+R5)J3 = -V3 \, [/math]
Prepisom do maticového tvaru dostaneme výsledný tvar sústavy rovníc. Jej riešením získame hodnoty slučkových prúdov J1,J2 a J3.
- [math] \left[ \begin{array}{ccc} {R1+R4} & -R4 & 0 \\ -R4 & {R2+R4+R5} & -R5 \\ 0 & -R5 & {R3+R5} \end{array} \right] \left[ \begin{array}{c} J1 \\ J2 \\ J3 \end{array} \right] = \left[ \begin{array}{c} V1 \\ 0 \\ -V3 \end{array} \right] [/math]
Výpočet obvodu
V interaktívnom móde Pythonu (konzola, iPython[2]) importujeme balík pylab pre vedecké výpočty a inicializujeme vstupné premenné hodnotami komponentov obvodu
>>> from pylab import *
>>> R1=4.0; R2=6.0; R3=8.0; R4=10.0; R5=10.0
>>> V1=12; V3=6
Vytvoríme maticu rezistancií obvodu a vektor zdrojov
>>> R=mat([[R1+R4, -R4, 0],[-R1, R2+R4+R5, -R5],[0, -R5, R3+R5]])
>>> V=mat([V1, 0, -V3])
Pre riešenie sústavy rovníc potrebujeme transponovať riadkový vektor napätí na stľpcový vektor.
>>> V=transpose(V)
Riešenie sústavy rovníc získame príkazom
>>> J=solve(R,V)
Hodnoty prúdov vetvami obvodu získame triviálnym výpočtom
>>> I1=J[1]
>>> I2=J[2]
>>> I3=J[3]
>>> I4=J[1]-J[2]
>>> I5=J[2]-J[3]