Generátor s komparátorom

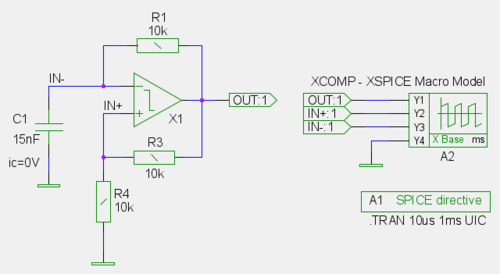
Generátor pravouhlého priebehu pozostáva z invertujúceho Schmittovho klopného obvodu tvoreného komponentami XCOMP, R₃, R₄ a dolnofrekvenčného filtra R₁, C₁.

Zapojenie obvodu

Kondenzátor sa nabíja cez odpor R₁ kladným napätím z výstupu komparátora. Keď potenciál v uzle IN- dosiahne kladnú komparačnú hodnotu Schmittovho klopného obvodu, tento sa skokom preklopí do opačnej zápornej polarity a v tomto stave zostane po dobu, kým napätie na uzle IN- nedosiahne zápornú komparačnú hodnotu. Obvod preklopí späť do kladnej polarity a celý cyklus sa opakuje.

Pre komparačné hodnoty Schmittovho klopného obvodu platí

[math] \begin{align} U_{ON} &= - \alpha \, U_{OUT} \\ U_{OFF} &= \alpha \, U_{OUT} \end{align} [/math]

Pre koeficient [math]\alpha[/math] platí

[math] \alpha = \frac {R_1} {R_1 + R_2} [/math]

Pre napätie U_C na kondenzátore platí diferenciálna rovnica

[math] \frac {d U_C} {dt} = \pm \frac {U_{OUT} - U_C} {R_1 C_1} [/math]

Pri riešení diferenciálnej rovnice predpokladajme počiatočnú podmienku, že kondenzátor sa začína nabíjať z dolnej komparačnej úrovne U_ON a celkové napätie na kondenzátore potom bude U_OUT+U_ON. Riešenie diferenciálnej má potom tvar

[math] \begin{align} U_{C}(t) &= \left( U_{OUT} + \alpha U_{OUT} \right) \left( 1 - e^{- \frac {t} {R_1 C_1} } \right ) - \alpha U_{OUT} \\ &= U_{OUT} \big[ 1 - \left( 1 + \alpha \right) e^{- \frac {t} {R_1 C_1} } \big] \end{align} [/math]

Dobu nabíjania kondenzátora z dolnej komparačnej úrovne do hornej získame riešením rovnice nabíjania kondenzátora pre neznámu hodnotu t₁ nasledujúcimi úpravami

[math] \begin{align} U_{OFF} &= U_{OUT} \big[ 1 - \left( 1 + \alpha \right) e^{- \frac {t_1} {R_1 C_1} } \big] \\ \alpha U_{OUT} &= U_{OUT} \big[ 1 - \left( 1 + \alpha \right) e^{- \frac {t_1} {R_1 C_1} } \big] \\ (1 -\alpha ) &= ( 1 + \alpha ) e^{- \frac {t} {R_1 C_1} } \\ t_1 &= R_1 C_1 ln \left( \frac { 1 + \alpha } {1 -\alpha } \right) \\ t_1 &= R_1 C_1 ln \left( 1 + \frac { 2 R_4 } { R_3 } \right) \end{align} [/math]

Perióda kmitov generátora je potom rovná

[math] T = 2 t_1 = 2 R_1 C_1 ln \left( 1 + \frac { 2 R_4 } { R_3 } \right) [/math]

Ak zvolíme hodnoty R₃=R₄, pre periódu kmitov platí

[math] T = 2 ln(3) \, R_1 C_1 = 2.2 R_1 C_1 [/math]

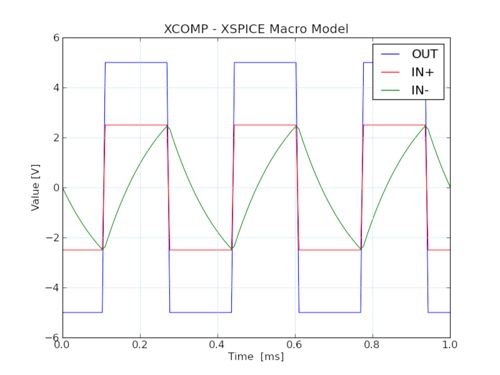
Simulované priebehy v uzloch IN+, IN- a na výstupe OUT generátora sú zobrazené na nasledujúcom obrázku.

Výsledok simulácie