Vzorkovací teorém

Vzorkovacia teoréma a spektrum vzorkovaného signálu

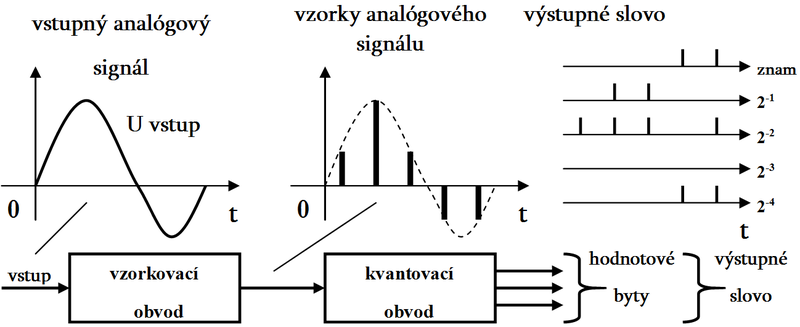
Obr. 1. Postup digitalizácie analógového signálu

Pred samotným odvodením vzorkovacej teorémy si najskôr ukážeme vhodnú metódu, ktorá predstavuje vzorkovanie časovo spojitého signálu v rovnomerných intervaloch. Na obr. 1 je postup digitalizácie analógového signálu. Užitočná je metóda použitia periodickej postupnosti Dirackových impulzov δ_T(t), ktorou vynásobíme časovo spojitý signál x(t). Tento spôsob známy ako ideálne vzorkovanie je znázornený na obr. 2. Periodická postupnosť δ_T(t) je označovaná ako vzorkovacia funkcia, perióda T ako vzorkovacia perióda a základná kruhová frekvencia ω₀=2π/T ako vzorkovacia kruhová frekvencia. Vzorkovacia teoréma určuje podmienku pre veľkosť periódy T medzi vzorkami rovnomerne časovo spojitého signálu.

Vzorkovacia teoréma

Každý časový priebeh x(t), ktorého modulované spektrum je frekvenčne zhora obmedzené kruhovou frekvenciou ωm=2πfm (nad touto frekvenciou je modulové spektrum spojitého signálu nulové)

[math]X(\omega) = \begin{cases} definovane\quad pre\big|\omega\big|\lt \omega_m\\ 0\qquad\qquad\qquad pre\big|\omega\big|\gt \omega_m \end{cases}[/math],

(1)

je jednoznačne určený svojimi hodnotami odoberanými v rovnomerných časových intervaloch

[math]T\le\frac{1}{2f_m}[/math],

(2)

kde T je perióda vzorkovania.

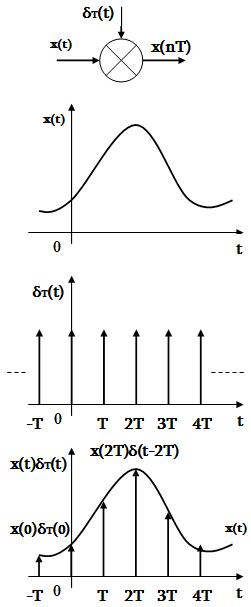
Obr. 2. Ideálne vzorkovanie

Táto vzorkovacia teoréma sa tiež niekedy označuje ako Nyquistova, Shannonova, alebo Koteľnikova teoréma.

Analógový signál x(t) sa vzorkuje každých T sekúnd T=1/2f_m alebo v intervaloch kratších ako T=1/2f_m sekúnd (T<1/2f_m). Z toho vyplýva, že tieto vzorky obsahujú informáciu o signáli x(t) pre každú z hodnôt t. Modulové spektrum vzorkovaného signálu musí potom obsahovať minimálne dvakrát vyššiu frekvenciu, než je medzná frekvencia f_m modulového spektra X(ω) spojitého signálu x(t).

Iným spôsobom povedané, analógový signál sa musí vzorkovať minimálne dvakrát v každej perióde jeho najvyššej frekvenčnej zložky alebo vzorkovacia frekvencia musí byť dvakrát vyššia ako je frekvencia analógového signálu.

Vzorkovaciu teorému dokážeme pomocou frekvenčnej konvolučnej teorémy. Uvažujeme analógový signál x(t), ktorého funkcia spektrálnej hustoty X(ω) je reálna a nemá žiadne rfekvenčné zložky nad ω_m (obr. 3 a). To znamená, že funkcia X(ω) je nulová pre |ω|>ω_m. Vynásobime signál x(t) periodickou postupnosťou jednotlivých impulzov δ_T(t). Výsledný signál bude postupnosť impulzov umiestnených v rovnomerných časových intervaloch T s veľkosťou x[nT] rovnajúcou sa hodnote x(t) v čase t=nT. Súčin x(t)δT(t) predstavuje vzorkovaný signál x_v(t), ktorý je vzorkovaný v rovnomerných intervaloch T (obr. 3 b):

[math]x_v=x(t)\delta_T(t)[/math].

(3)

Funkciou spektrálnej hustoty signálu x(t) je X(ω) a Fourierov obraz δ_T(t) je ω_vδω_v(ω), kde ω_v=2π/T. Na základe frekvenčnej konvolučnej teorémy platí:

[math]x(t)\longleftrightarrow\overline{X}(\omega)[/math], [math]\delta_T(t)=\sum_{n=-\infty}^\infty\delta(t-nT)\longleftrightarrow\omega_v\delta_\omega v(\omega)=\omega_v\sum_{n=-\infty}^\infty\delta(\omega-n\omega_v)[/math], [math]x_v(t)=x(t)\delta_T(t)\longleftrightarrow\overline{X_v}(\omega)=\frac{1}{2\pi}\Big[\overline{X}(\omega)\ast\omega_v\delta_\omega v(\omega)\Big][/math].

(4)

Po úprave (4):

[math]x_v(t)\longleftrightarrow\overline{X_v}(\omega)=\frac{1}{T}\Bigr[\overline{X}(\omega)\ast\delta_\omega v(\omega)\Bigr][/math],

(5)

kde

[math]\overline{X_v}(\omega)=\Im\big\{x_v(t)\big\}[/math].

(5-2)

Vzťah (5) je znázornený na obr. 3 c. Vidíme, že X_v(ω) sa opakuje s periódou ω_v, ktorá musí spĺňať podmienku:

[math]x_v\ge2\omega_m\rArr\frac{2\pi}{T}\ge4\pi f_m[/math],

(6)

z čoho vyplýva:

[math]T\le\frac{1}{2f_m}[/math].

(6-2)

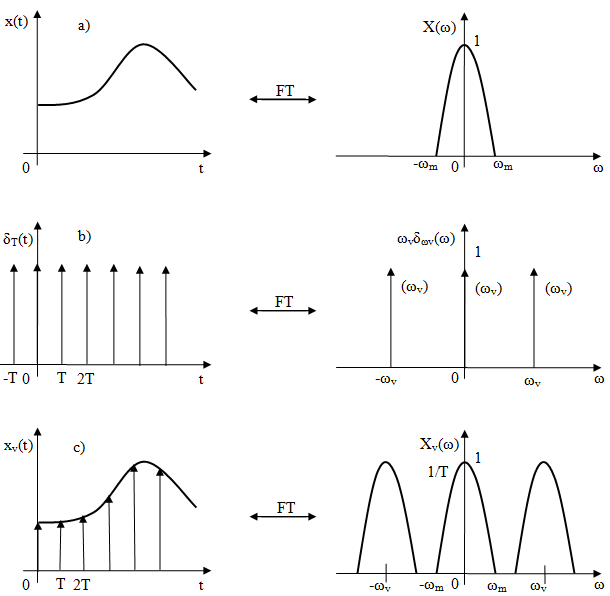
Obr. 3. Periodické (rovnomerné) vzorkovanie analógového signálu

Spektrum X_v(ω) vzorkovaného signálu x_v(t) odvodíme zo vzťahu (5):

[math]\overline{X_v}(\omega)=\frac{1}{T}\Big[\overline{X}(\omega)*\delta_\omega v(\omega)\Big]=\frac{1}{T}\Bigg[\overline{X}(\omega)*[\sum_{n=-\infty}^\infty\delta(\omega-n\omega_v)\Bigg]=\frac{1}{T}\sum_{n=-\infty}^\infty\Big[\overline{X}(\omega-n\omega_v)\Big][/math]

(7)

Zo vzťahu (7) a z obr. 3.c vidno, že ak vzorkujeme signál x(t) v rovnomerných časových intervaloch T≤1/2f_m sekúnd, potom funkcia spektrálnej hustoty vzorkovaného signálu x_v(t) (t.j. „ideálnych vzoriek“) obsahuje všetky informácie o X_v(ω), a tým aj o pôvodnom signáli x(t). Ideálne vzorky sú plne určené periódou vzorkovania a obyčajnými vzorkami . Preto aj množina obyčajných vzoriek obsahuje informáciu o celom časovom priebehu frekvenčne obmedzeného signálu x(t).

Frekvencia

[math]f_v=\frac{1}{T}=2f_m[/math]

(7-2)

sa nazýva Nyquistova frekvencia (rýchlosť) alebo kritická frekvencia vzorkovania pre frekvenčne obmedzený signál.

Periodické alebo rovnomerné vzorkovanie je opísané vzťahom

[math]x\big[n\big]=x\big[nT\big]\quad pre\quad n\isin(-\infin;\infin)[/math]

(7-3)

Proces periodického vzorkovania je znázornený na obr. 4.

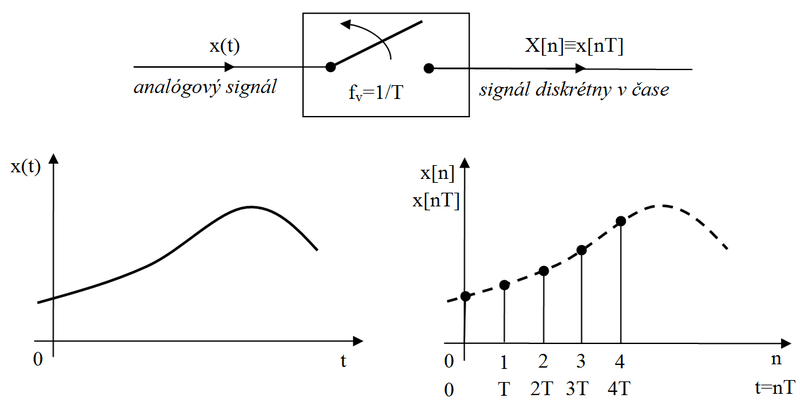
Obr. 4. Proces periodického vzorkovania

Periodické vzorkovanie určuje vzájomný vzťah medzi časovými premennými t a n signálu spojitého a diskrétneho v čase. Tieto premenné sú vzájomne lineárne viazané cez periódu vzorkovania alebo rýchlosť vzorkovania f_v=1/T vzťahom:

[math]t=nT=\frac{n}{f_v}[/math]

(7-4)

Zdroj literatúry

[1]. ONDRÁČEK, Oldřich. Diskrétne signály a sústavy. 1. vyd. 2002. ISBN 80-227-1649-9.

[2]. ONDRÁČEK, Oldřich. Signály a sústavy. 1. vyd. 1999. ISBN 80-227-1254-X.

Ďalšia literatúra:

[1]. Základy číslicového merania: http://webmail.stuba.sk/~peter.kukuca/pedagogika/ADC2003.doc

[2]. Signály: http://sdelovacka.kbx.cz/data/statnice/BEST/20.pdf

[3]. Číslicové meranie: http://www.kukuca.sk/Meranie/Meranie-P-02.pdf

[4]. FEI STU-KMER :http://www.kmer.elf.stuba.sk/index.php?searchword=vzorkova&option=com_search&Itemid=