D/A Prevodník R^n

D/A Prevodník R^n

Prevodníky s odporovou sieťou R_N, patrí medzi paralelné D/A prevodníky, ktoré využívajú metódu váhovania.

Paralelné D/A prevodníky sa vyznačujú tým, že koeficienty a₁ – a_n číslicového vstupného slova sú k dispozícii súčasne. Hodnotám 0 a 1 týchto koeficientov zodpovedajú polohy prepínačov D/A prevodníka. Rýchlosť prevodu paralelných D/A prevodníkov môže byť veľmi vysoká. Určuje ju doba zopnutia a rozopnutia analógových spínačov, trvanie prechodných javov v odporovej sieti prevodníka a rýchlosť sumačného zosilňovača. Doba ustálenia bežných D/A prevodníkov sa udáva v jednotkách až desiatkach mikrosekúnd, rýchle D/A prevodníky dosahujú hodnoty rádovo jednotiek až desiatok nanosekúnd.

Obr. 1 D/A prevodník so sčítavaním prúdov

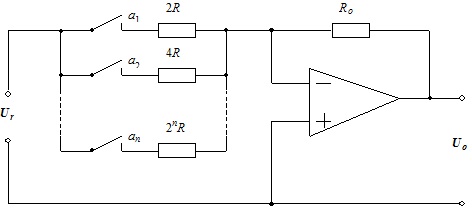
Principiálne najjednoduchší paralelný D/A prevodník používa metódu sčítavania (váhovaných) prúdov podľa obr. 1. Pre výstupné napätie prevodníka platí

[math]U_o =U_r.R_0 \sum_{i=1}^N \frac{a_i}{2^i.R}[/math]

Ak R₀ = R , potom sa tento vzťah zmení na tvar

[math]U_o =-R_f(i_7b_7+...+i_0b_0)= -\frac{R_F}{R}.U_{REF} (b_7 + \frac{b_6}{2}+\frac{b_5}{4}+\frac{b_4}{8}+\frac{b_3}{16}+\frac{b_2}{32}+\frac{b_1}{64}+\frac{b_0}{128})[/math]

to znamená, že plný rozsah D/A prevodníka (FSR) je v takomto prípade rovný hodnote referenčného napätia U_r.

Hlavným nedostatkom D/A prevodníkov so sčítavaním prúdov je veľký rozsah hodnôt odporov, čo spôsobuje problémy pri ich realizácii, ale najmä horšiu teplotnú a časovú stabilitu, a teda menšiu presnosť týchto prevodníkov.

Obr. 2 zapojenie váhového 8-bitového D/A prevodníka

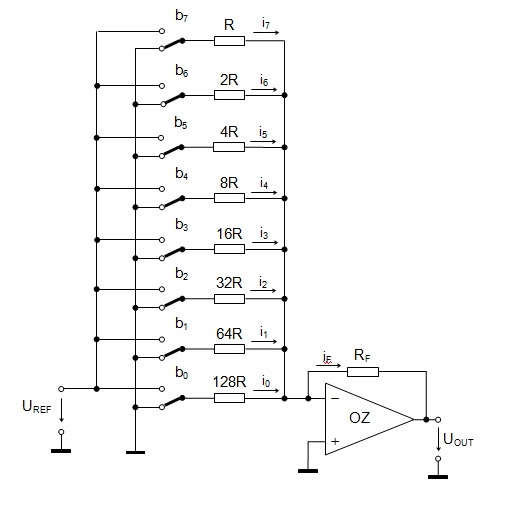
Na obrázku 2 je znázornené zapojenie 8-bitového D/A prevodníka. Z vlastnosti ideálneho operačného zosilňovača vyplýva

[math]i=i_7b_7 + i_6b_6 + i_5b_5 + i_4b_4 + i_3b_3 + i_2b_2 + i_1b_1 + i_0b_0 = -\frac{U_0}{R_f}[/math] ,

kde b_n=1 pre zapnutý vypínač a b_n=0 , pre vypnutý vypínač.

[math]i_7 = \frac{U_{REF}}{2^0.R}, i_6 = \frac{U_{REF}}{2^1.R},... i_n = \frac{U_{REF}}{2^{7-n}}[/math]

A z toho:

[math]U_0 = -R_f(i_7b_7+...+i_0b_0)=-\frac{R_F}{R} U_{REF}(b_7+\frac{b_6}{2}+\frac{b_5}{4}+\frac{b_4}{8}+\frac{b_3}{16}+\frac{b_2}{32}+\frac{b_1}{64}+\frac{b_0}{128})[/math]

[math]U_0=-\frac{R_F}{R} U_{REF}\sum_{n=0}^7 \frac{b_n}{2^{7-n}}[/math]

Koeficienty 2ⁿ určujú váhu jednotlivých rezistorov. Rezistor s najmenšou váhou je 2⁷R (preteká ním najmenší prúd) a s najväčšou je 2⁰R . LSB je bit s najmenšou váhou a MSB je bit s najväčšou váhou. Presnosť prevodníka ovplyvňuje stabilita referenčného napätia U_{REF} a teplotná stabilita odporovej siete. V prvom rade sa musia dodržať presné hodnoty odporov, čo sa ťažšie realizuje.

Z toho dôvodu sa častejšie využívajú prevodníky realizované pomocou rezistorovej siete R-2R.