Chyby prevodníkov
Chyby ČAP
Chyby reálneho ČAP možno rozdeliť na
1. chybu nuly,
2. chybu zosilnenia,
3. chybu linearity: - integrálnu nelinearitu, - diferenciálnu nelinearitu.
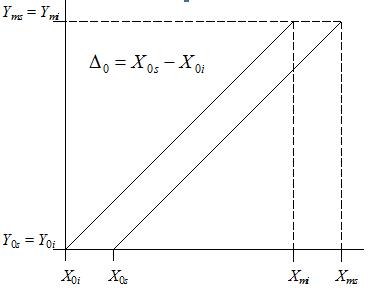
Chyba nuly ČAP Δ0 je definovaná ako posunutie prevodovej charakteristiky voči ideálnej nahor alebo nadol. Zistí sa ako rozdiel medzi skutočnou a ideálnou hodnotou výstupného napätia ČAP pri nulovej vstupnej hodnote.
Δ0 = Y0s – Y0i
Pretože ideálna hodnota výstupu je vo väčšine prípadov nulová, chyba nuly ČAP je väčšinou rovná priamo hodnote výstupu pri nulovom vstupe.
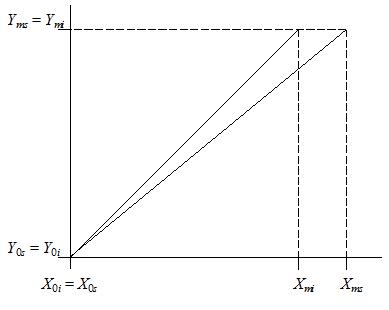
Chyba zosilnenia δz je definovaná ako rozdiel medzi smernicou skutočnej a ideálnej prevodovej charakteristiky ČAP. Platí teda:
[math]\delta_z =\frac{Y_ms - Y_0s}{X_ms - X_0s} - \frac{Y_mi - Y_0i}{X_mi - X_0i}[/math]
Pretože vstup ČAP je číslicový a vždy „správny“, nemá zmysel rozlišovať skutočné a ideálne hodnoty vstupu ČAP. Predchádzajúci vzorec si čitateľ ľahko upraví na tvar:
[math]\delta_z =\frac{Y_ms - Y_mi - δ 0}{X_m - X_0}[/math]
Nelinearita, čiže chyba linearity sa vyjadruje dvoma spôsobmi, ktoré tú istú krivosť prevodovej charakteristiky vyjadrujú dvoma rôznymi spôsobmi. Hodnoty týchto dvoch nelinearít sa nedajú navzájom prepočítať.
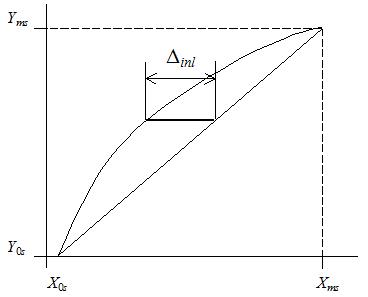
Integrálna nelinearita Δinl je maximálny rozdiel medzi skutočnou prevodovou charakteristikou a jej priamkovou náhradou. Priamková náhrada je najčastejšie tvorená úsečkou spájajúcou koncové body skutočnej prevodovej charakteristiky.
Diferenciálna nelinearita Δdnl je maximálny rozdiel medzi skutočným a ideálnym krokom kvantovania. Je to vlastne najväčšia odchýlka (v absolútnej hodnote) „šírky schodíka“ prevodovej charakteristiky od jej ideálnej hodnoty q.
Na zistenie zložiek chyby ČAP stačí odmerať prevodovú charakteristiku testovaného ČAP. Postup výpočtu si čitateľ podľa predchádzajúcich vzorcov a definícií urobí sám.
Chyby AČP
Ako bolo uvedené už skôr, aj ideálny („bezchybný“) AČ prevodník vnáša do AČ prevodu chybu, a to chybu kvantovania. K tejto chybe danej samotným faktom prevodu spojitej veličiny na diskrétnu pribúdajú v reálnych prevodníkoch nedokonalosti ich konkrétnej realizácie. Z hľadiska ich prejavu a možnosti ich odstránenia alebo korekcie delíme chyby AČP na:
1. chybu nuly,
2. chybu zosilnenia,
3. chybu linearity: - integrálnu nelinearitu, - diferenciálnu nelinearitu.
Hoci delenie chýb AČ prevodníkov je rovnaké jako u ČA prevodníkov a dokonca aj definičné vzťahy sú podobné, prípadne až zhodné, zistenie týchto chýb je pri AČ prevodníkoch trochu iné a podstatne pracnejšie.
Pretože výstupné hodnoty AČP sú jednoznačné diskrétne hodnoty (čísla) a vstupná spojitá veličina môže nadobúdať ľubovoľné hodnoty, chyby AČP sa vzťahujú na vstupnú spojitú veličinu, resp. určujú sa pomocou odchýlok vstupných hodnôt od indikovaných výstupných hodnôt AČP.
Chyba nuly Δ0 sa prejavuje posunutím prevodovej charakteristiky AČP, chyba zosilnenia δz znamená odchýlku sklonu prevodovej charakteristiky od ideálu. Pri zjednodušení prevodovej charakteristiky AČP na spojitú krivku sú tieto chyby znázornené na obr. 1 a obr. 2, pričom platia v nich uvedené vzťahy. Index i znamená ideálnu (teoretickú) charakteristiku, index s skutočnú charakteristiku AČP.
Chyba linearity vyjadruje krivosť skutočnej prevodovej charakteristiky jedným z dvoch spôsobov – ako integrálnu nelinearitu alebo ako diferenciálnu nelinearitu.
Integrálna nelinearita Δinl je maximálny rozdiel medzi skutočnou prevodovou charakteristikou a jej priamkovou náhradou. Priamková náhrada je najčastejšie tvorená úsečkou spájajúcou koncové body skutočnej prevodovej charakteristiky. Integrálna nelinearita je ilustrovaná na obr. 3.
Diferenciálna nelinearita Δdnl je maximálny rozdiel medzi skutočným a ideálnym krokom kvantovania. Je to vlastne najväčšia odchýlka (v absolútnej hodnote) „šírky schodíka“ prevodovej charakteristiky AČP od jej ideálnej hodnoty q.
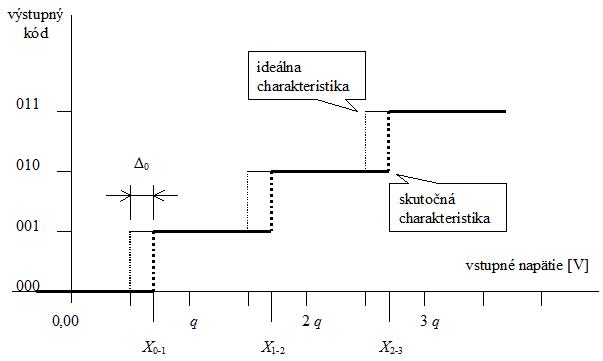
A teraz, ako je to naozaj: Pretože prevodová charakteristika AČP je nespojitá tak, že jej jednotlivým výstupným hodnotám (kódom) zodpovedajú intervaly vstupných hodnôt, pri zisťovaní chýb AČP (resp. pri meraní prevodovej charakteristiky AČP) je potrebné zistiť (odmerať) vstupné hodnoty, pri ktorých dochádza ku zmene výstupného kódu. To je jednak piplačka (časovo náročná úloha), na druhej strane to znamená potrebu upresniť zjednodušené obrázky 1 a 2.