Rekurzia

Rekurzia (po latinsky: recurrere = bežať naspäť) je matematike a informatike využitie časti vlastnej vnútornej štruktúry. V definícii funkcie sa nachádza volanie samotnej funkcie. Inak povedané, funkcia volá samú seba.

Rekuzia - definície, princípy

Rekurzia v grafike

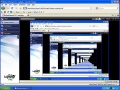
Najjednoduchsim prikladom rekuzie, ktorý sa dá zobraziť je dať 2 zrkadlá oproti sebe (Obr. 1). Ďalším príkladom môže byť spustenie programu vzdialená pracovná plocha, kde adresa vzdialeného počítača bude ten počítač, na ktorom bola aplikácia spustená (Obr. 2). Rekurzia sa občas objaví i na obaloch potravín (Obr. 3).

• 

  Obr. 1 Rekurzívny obraz v zrkadlách

• 

  Obr. 2 Rekurzívny obraz ´vzdialenej´ pracovnej plochy

• 

  Obr. 3 Rekurzívny obal kakaa

Rekurzia v názvoch vecí

Pracujeme z názvami a skratkami, ktoré sú už také zaužívané, že ani nerozmýšľame čo znamenajú. Čo znamenajú skratky GNU, wine (program v linuxe, nie víno), PNG, LAME (mp3 enkodér), PHP, YAML, VISA ....

• PNG - Oficiálne "Portable Network Graphics", Neoficiálne "PNG is Not Gif"
• LAME - LAME Ain't an MP3 Encoder
• Wine -Wine Is Not an Emulator
• PHP - PHP: Hypertext Preprocessor
• YAML - YAML Ain't Markup Language
• VISA - Visa International Service Association
• GNU - GNU's Not Unix

Slovná definícia pojmu Rekurzia

pozri Rekurzia

Zoznam viacerých skratiek je v anglickej verzii wikipédie .

Rekurzia v matematike

Prirodzené čísla

Prirodzené čísla definujme nasledovne:

• 0 patrí do množiny [math]\mathbb{N}[/math]
• ak patrí n do množiny [math]\mathbb{N}[/math], potom n + 1 patrí tiež do množiny [math]\mathbb{N}[/math]

Množina prirodzených čísel je taká najmenšia množina reálnych čísel, ktorá spĺňa 2 predchádajúce kritériá.

Prvočísla

Prvočísla definujme ako:

• Číslo 2 je najmenšie prvačíslo.
• Prvočíslo je každé celé kladné číslo, ktoré nie je deliteľné žiadnym iným menším prvočíslom ako je toto číslo samotné.

Katalánske čísla

• [math]C_0=1[/math]
• [math]C_{n+1}=\frac{(4n+2)C_n}{n+2}[/math]

Ackermanova funkcia

Ackermanova funkcia je príklad neprimitívnej rekurzívne definovanej funkcie, ktorá veľmi rýchlo rastie. Pre kladné m, n môžeme Ackermanovu funkciu vyjadriť nasledokvne: [math] A(m,n) = \begin{cases} n+1, & ak\ m=0 \\ A(m-1,1), & ak\ m\gt 0,\ n=0 \\ A(m-1,A(m,n-1)), & ak\ m\gt 0,\ n\gt 0 \end{cases} [/math] Už pre malé hodnoty m a n dosahuje veľkých hodnôt. Napríklad A(4,2) je celé číslo, ktoré má 19 729 cifier.

Rekurzia v informatike

Princíp fungovania rekurzívnych funkcií:

• Zložitý problém môžeme riešiť rekurzívnym spôsobom tak, že:
  • Daný problém rozložíme na elementárne podproblémy, ktoré dokážeme jednoducho vyriešiiť.
  • Tieto podproblémy musia byť rovnakého typu.
  • Riešenie spočíva v opakovanom (rep. rekurzívnom) vykonávaní funkcie riešiacej daný problém.
  • Dôležitou bodom je určiť podmienku, kedy sa ukončí riešenie úlohy.

Príklad: Vypíšte za sebou čísla od n do 0. Nech n=5

Zložitý´ problém

vypísať dané čísla: (Dajme tomu, že nepoznám cykly)

Rozloženie problému na elementárne podproblémy

vypíšem len jedno číslo (to viem)

Podmienka ukončenia výpisu

Prestanem keď vypíšem posledné číslo - 0

Doterajšie riešenie

Funkcia, ktorý vypíše len jedno číslo (n)

void vypis(int n) { cout<<n; }

Doplnenie rekurzie

Vo funkcii vypis pridam volanie funkcie vypis, ktorá má parameter n o 1 menší

void vypis(int n) { cout<<n; vypis(--n); }

Analýza riešenia

Vyrobili sme deadlock, čiže uviaznutie programu. Funckia vypis sa nikdy neukonci, bude sa volať do nekonečna (resp. dotiaľ, dokiaľ bude mať program dostatok pamäti. Potom spadne).

Doplnenie ukončujúcej podmienky

Vypisovanie ukončím pri výpise 1.

void vypis(int n) {
 cout<<n; 
 if(n>0) 
   vypis(--n); 
}

Typy rekurzie

Pravá rekurzia

nastane, ak sa za rekurzívnym volaním nachádzajú ešte nejaké príkazy alebo ak rekurzívne voláme na viacerých miestach programu. Takýto prechod na nerekurzívny algoritmus je zložitejší a často až nereálny.

Chvostová rekurzia

inak nazývaná nepravá alebo jednoduchá. Nastane vtedy, keď rekurzívna procedúra volá samu seba ako svoj posledný príkaz. Takáto rekurzia sa veľmi ľahko dá prepísať na cyklus.

Ukážky rekurzívne definovaných funkcií

Faktoriál

Definícia:

• 0!=1
• n!=n*(n-1)!

Pri tvorbe funkcie pre výpočet faktoriálu budeme postupovať presne podľa rekurzívnej definície:

long faktorial(int n) {
 if(n==0) return 1; // 0!=1
 return n*faktorial(n-1); // n!=n*(n-1)!
}

Fibonacciho postupnosť

Definícia:

• Fib(0)=0
• Fib(1)=1
• Fib(i)=Fib(i-1)+Fib(i-2), pre i>1

Rovnako aj tu budeme postupovať presne podľa rekurzívnej definície:

long fibonacci(int n) {
 if(n<2) return n; // fib(0)=0, fib(1)=1
 return fibonacci(n-1)+fibonacci(n-2); // fib(n)=fib(n-1)+fib(n-2)
}

Najväčší spoločný deliteľ

Najväčší spoločný deliteľ , dvoch celých čísel m,n rieši Euklidov algoritmus. Jeho najjednoduchšia forma sa dá popísať nasledovne:

1. vstupné hodnoty: m, n
2. Ak je m=n, tak koniec (krok 6)
3. ak je m>n, tak m=m-n
4. ak je n>m, tak n=n-m
5. skok na krok 2
6. NSD(m,n)=m (keďze m a n sú rovanké je jedno, ktorú premennú budeme považovať za výsledok)

NSD vieme definovať aj rekurzívne:

• [math]NSD(m,0)=\ m[/math]
• [math]NSD(m,n)=NSD(n,m\ \mbox{mod }n)[/math]

V jazyku C to môžeme zapísať nasledovne:

long nsd(int m, int n) {
 if(n==0) return m; 
 return nsd(n,m%n);
}

Hanoiské veže

Hlavolam / Hanojské veže

Hanojské veže je matematický hlavolam. Skladá sa z troch kolíkov (veží). Na začiatku je na jednom z nich položených niekoľko kotúčov rôznych polomerov, zoradených od najväčšieho (naspodku) po najmenší (hore). Úlohou riešiteľa je premiestniť všetky kotúče na druhú vežu (tretiu pritom využije ako pomocnú pre dočasné odkladanie) podľa nasledujúcich pravidiel:

• V jednom ťahu sa dá premiestniť len jeden kotúč
• Jeden ťah pozostáva zo vzatia vrchného kotúča z niektorej veže a jeho položenie na vrchol inej veže.
• Je zakázané položiť väčší kotúč na menší.

Jednoduché riešenie

Striedavo sa presúva najmenší kotúč a iný kotúč ako najmenšie. Ak sa presúva najmenší kotúč, potom sa vždy presunie o jednu vežu ďalej v stále rovnakom smere, a to doprava pri celkovom párnom počte kotúčov a doľava pri nepárnom (predpokladáme, že veže stoja v rade vedľa seba, počiatočné je najviac vľavo a cieľové najviac vpravo). Ak je už najmenší kotúč na poslednej veži v tomto smere, presunie sa na vežu na opačnom konci. Ak má byť presunutý iný kotúč ako najmenší, je to možné vykonať vždy len jediným spôsobom. Týmto spôsobom možno hlavolam vyriešiť na najmenší možný počet ťahov.

Rekurzívne riešenie

Riešenie pomocou rekurzie vychádza z úvahy, že riešenie musí obsahovať najmenej jeden ťah, v ktorom je presunutý najväčší kotúč. Ten však možno presunúť len vtedy, keď sú všetky ostatné kotúče nasadené na tretej veži. Označme počet kotúčov n. Najprv teda presunieme n-1 kotúčov (všetky okrem najväčšieho) na odkladaciu vežu, potom presunieme najväčší kotúč z počiatočnej veže na cieľovú a nakoniec presunieme n-1 kotúčov z odkladacej veže na cieľovú. Presun n-1 kotúčov však môžeme vykonať pomocou rekurzívneho volania tohto algoritmu pre n-1 kotúčov, pretože najväčší kotúč nám pritom nebráni (na neho môžeme položiť akýkoľvek iný, takže môžeme postupovať, ako by nebol). Presný postup je teda nasledovný:

1. Ak je n > 1, potom rekurzívnym volaním tejto procedúry presunieme n-1 kotúčov (t.j. všetky okrem najväčšieho) z počiatočnej veže na odkladaciu.
2. Presunieme najväčší kotúč z počiatočnej veže na cieľovú.
3. Ak je n > 1, potom rekurzívním volaním tejto procedúry presunieme n-1 kotúčov z odkladacej veže na cieľovú.

Implementácia rekurzívneho algoritmu v jazyku C:

void Hanoj(int n,char zaciatocna, char cielova, char pomocna)
{
    if (n>1)
      Hanoj(n-1, zaciatocna, pomocna, cielova);
    printf("%c => %c \n", zaciatocna,cielova);
    if (n>1)
     Hanoj(n-1, pomocna, cielova, zaciatocna);
}

Po zavolaní funkcie

Hanoj(4,'A','B','C');

dostaneme výpis:

A => C 
A => B 
C => B 
A => C 
B => A 
B => C 
A => C 
A => B 
C => B 
C => A 
B => A 
C => B  
A => C 
A => B 
C => B