Termodynamický dej

Termodynamický dej (taktiežtepelný dej) je dej, pri ktorom sa mení stav telesa (mení sa niektorá zo stavových veličín).

Kruhový dej

Pokiaľ termodynamická sústava prejde radou zmien a nakoniec sa vráti do pôvodného stavu, potom hovoríme, že sústava vykonala kruhový dej (cyklus).

= dej, pri ktorom je konečný stav sústavy totožný s počiatočným stavom. Obsah plochy vnútri krivky ( v diagramu pV) znázorňuje celkovú prácu W´ vykonanú behom jedného cyklu. W´ = Q = Q1 – Q2 Celková zmena vnútornej energie po ukončení jedného cyklu je nulová ( ΔU = 0)

Vratné a nevratné deje

Termodynamické deje môžeme rozdeliť na

• Vratné (reverzibilní) deje - Vratné deje sú také, u ktorých možno pôvodného stavu dosiahnuť obrátením poradí jednotlivých úkonov.
• Nevratné (ireverzibilné) deje - Nevratné deje sú také deje, ktoré prebiehajú bez vonkajšieho pôsobenia len v jednom smere, teda pôvodného stavu nemožno dosiahnuť presne rovnakým postupom v obrátenom poradí. K dosiahnutiu pôvodného stavu je nutné vynaložiť určitú energiu, ktorá nepatrí danej sústave. V prírode sú všetky reálne deje nevratné.

Kruhové deje bývajú označované ako vratné alebo nevratné cykly. Najznámejším príkladom vratného kruhového deja je Carnotov cyklus.

Deje pri konštantnej termodynamickej veličine

Mnohé technicky využiteľné deje prebiehajú tak, že niektorá z termodynamických veličín zostává behom deja konštantná. Také deje bývajú označované špeciálnymi názvami.

Konštantná veličina	Názov deja
Teplota	Izotermický dej
Tlak	Izobarický dej
Objem	Izochorický dej
Teplo	Adiabatický dej
Entropia	Izoentropický dej
Entalpia	Izoentalpický dej

Všeobecná rovnice zmeny stavu plynu

Z podobnosti vzťahov pre izotermický, adiabatický a polytropický dej možno zapísať všeobecnou rovnicou pre zmenu stavu plynu v tvare

[math]pV^k = \mbox{konst} \,[/math],

kde [math]p[/math] je tlak plynu, [math]V[/math] je jeho objem a [math]k[/math] je konštanta.

Pre [math]k=1[/math] sa jedná o vzťah pre izotermický dej, pre [math]k[/math] rovné Poissonovej konštante [math]\kappa[/math] ide o adiabatický dej. Ak zvolíme [math]k=n\in(1,\kappa)[/math], jedná sa o polytropický dej. Pre [math]k=0[/math] sa jedná o rovnicu izobarického deja a pre [math]k\to\pm\infty[/math] ide o izochorický dej.

Deje v plynoch v rôznych diagramoch

Tieto deje v plynoch sa dajú zapísať do týchto troch rôznych diagramov:

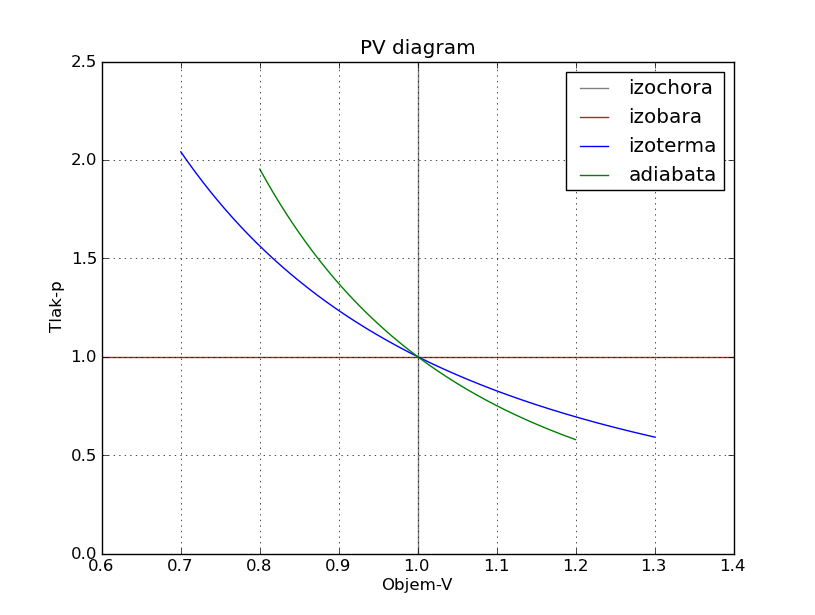
PV diagram:

from pylab import  *

ylim((0.5,2.3))
axvline(x=1, color="gray")
axhline(y=1, color="brown")
 x1=linspace(0.7,1.3,10000)
 x2=linspace(0.8,1.2,10000)
y1=x1**(-2)
y2=x2**(-3)
plot(x1,y1,x2,y2)
title("PV diagram")
legend(("izochora", "izobara", "izoterma", "adiabata"))
xlabel ("Objem - V")
ylabel ("Tlak - p")
grid(1)
show()

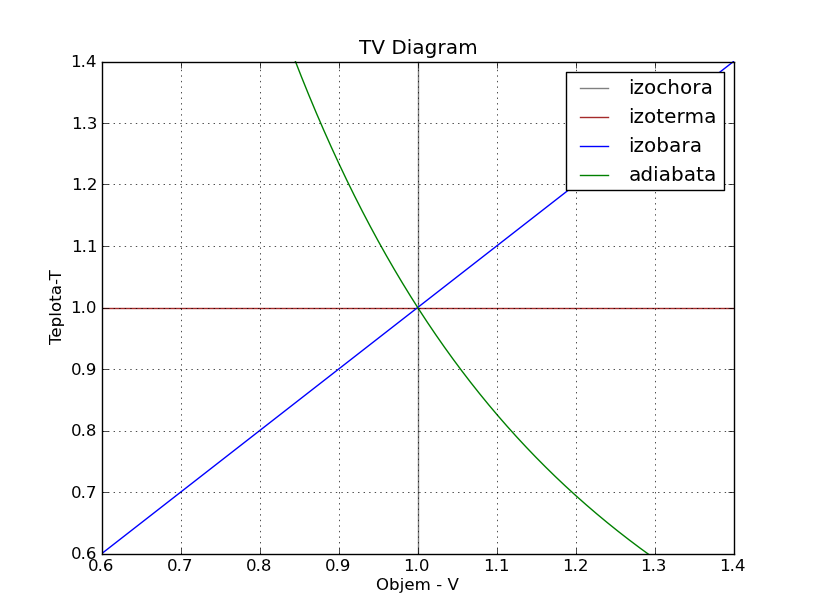
TV diagram:

 from pylab import  *

 ylim((0.6,1.4))
 xlim((0.6,1.4))
 axvline(x=1, color="gray")
 axhline(y=1, color="brown")
 x1=linspace(0.2,1.4,10000)
 x2=linspace(0.8,1.6,10000)
 y1=x1
 y2=x2**(-2)
 plot(x1,y1,x2,y2)
 title("TV Diagram")
 legend(("izochora","izoterma","izobara","adiabata"))
xlabel("Objem - V")
 ylabel("Teplota - T")
 grid(1)
 show()

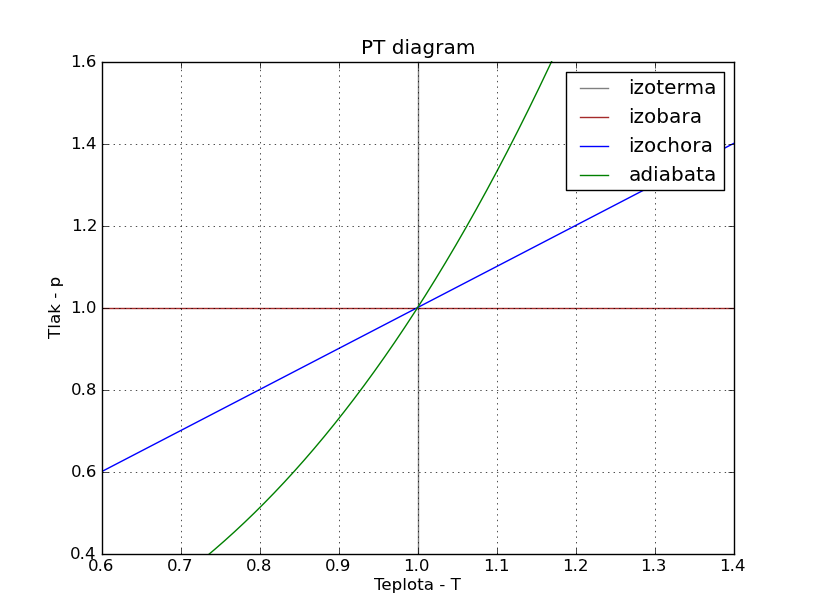
PT diagram:

 from pylab import  *

 xlim((0.6,1.4))
 ylim((0.4,1.6))
 axvline(x=1, color="gray")
 axhline(y=1, color="brown")
 x1=linspace(0.2,1.4,10000)
 x2=linspace(0.6,1.6,10000)
 y1=x1
 y2=x2**3
 plot(x1,y1,x2,y2)
 title("PT diagram")
legend(("izoterma","izobara", "izochora", "adiabata"))
 xlabel("Teplota - T")
 ylabel("Tlak - p")
grid(1)
 show()