Výpočet elektrického poľa metódou konečných diferencií
Tento program som napísal ako projekt ku predmetu Pokročilé programovanie na FMFI UK. Úloha ktorú som si stanovil, bola použitie metódy konečných diferencii na vypočítanie priebehu elektrického poľa.
Metóda konečných diferencii je jednoduchá numerická metóda, ktorá spočíva v diskretizovaní zadanej úlohy a jej riešení v jednotlivých strategicky zvolených bodoch. V našom prípade diskretizujeme riešenie dvojrozmernej Poissonovej rovnice na výpočet elektrického poľa.
Tá má tvar: [math]\frac{\partial^{2} U}{\partial x^2} + \frac{\partial^{2} U}{\partial y^{2}} = - \frac{Q}{\kappa} [/math]
Zvolíme si vhodné rozloženie bodov na diskretizáciu. Vhodným rozložením na riešenie „hranatej“ úlohy, je pravouhlá mriežka.
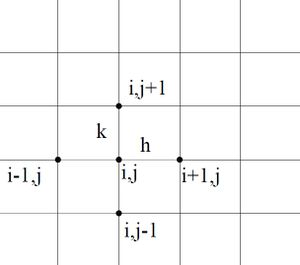
Aproximácia problému touto metódou spočíva v nahradení derivácii v jednotlivých bodoch siete diferenciáciou. Potom je hľadaná veličina v bode vypočítaná z hodnôt veličiny v okolitých bodoch. Hodnota potenciálu v bode i, j sa vyjadrí podľa hodnôt v bodoch x+h a x-h (analogicky tiež y+k, y-k) , ktoré sa rozvinú do Taylorovho radu. Úpravami týchto rozvojov dostaneme vyjadrenie druhej derivácie potenciálu v bode i,j v závislosti od hodnôt potenciálu vedľajších bodov v x-ovom alebo y-ovom smere a od hodnoty v bode i,j.
Dostaneme: [math]U''_{i,j}=\frac{U_{i+1,j}-2U_{i,j}+U_{i-1,j}}{h^{2}}[/math] a [math]U''_{i,j}=\frac{U_{i,j+1}-2U_{i,j}+U_{i,j-1}}{k^{2}}[/math]
Tieto rovnice sú aproximáciou druhých parciálnych derivácii potenciálov podľa x a y. Boli však vyjadrené zanedbaním členov Taylorovho rozvoja s mocninou 3 a viac. Chyba aproximácie bude teda rádu h2 resp. k2.
Dostali sme teda: [math]\frac{\partial^{2}U}{\partial x^2} = \frac{U_{i+1,j}-2U_{i,j}+U_{i-1,j}}{h^{2}}[/math] a [math]\frac{\partial^{2}U}{\partial y^2} = \frac{U_{i,j+1}-2U_{i,j}+U_{i,j-1}}{k^{2}}[/math]
Po doplnení do základnej rovnice: [math]\frac{1}{h^{2}}({U_{i+1,j}-2U_{i,j}+U_{i-1,j}}) + \frac{1}{k^{2}}({U_{i,j+1}-2U_{i,j}+U_{i,j-1}}) + Q = 0[/math]
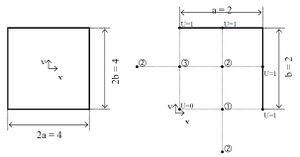
Samotná úloha pozostáva zo zistenia priebehu potenciálu vnútri prierezu štvorcového koaxiálneho vodiča. Vnútorný vodič môže mať potenciál rovný 0. Potenciál na vonkajšom plášti môžeme pre jednoduchosť nahradiť 100% čiže 1.
V závislosti od požadovanej presnosti výpočtu rozdelíme vnútro jedného kvadrantu vodiča (úloha je symetrická) na indexované body. Indexy priradíme iba bodom ktoré majú neznámy potenciál.