Chaotické riešenie diferenciálnych rovníc - Lorenzov atraktor
Skočit na navigaci
Skočit na vyhledávání
Lorenzova sústava[1] diferenciálnych rovníc má tvar
[math] \frac{d x}{d t} = s(y-x) [/math]
[math] \frac{d y}{d t} = rx -y - xz [/math]
[math] \frac{d z}{d t} = xy - bz [/math]
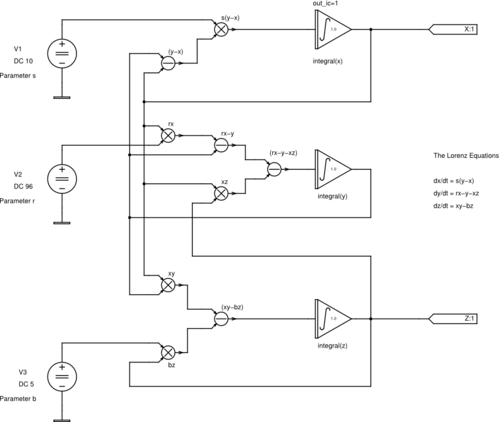
Sústava rovníc vykazuje pri vhodnom výbere vstupných parametrov r,s,b chaotické nedeterministické riešenie. Simulačný model vytvoríme priamym prepisom sústavy rovníc do grafickej podoby pomocou komponentov Xspice. Pre nastavenie hodnôt parametrov r,s,b boli použité zdroje napätia.
|
| Simulačný model[2][3] |
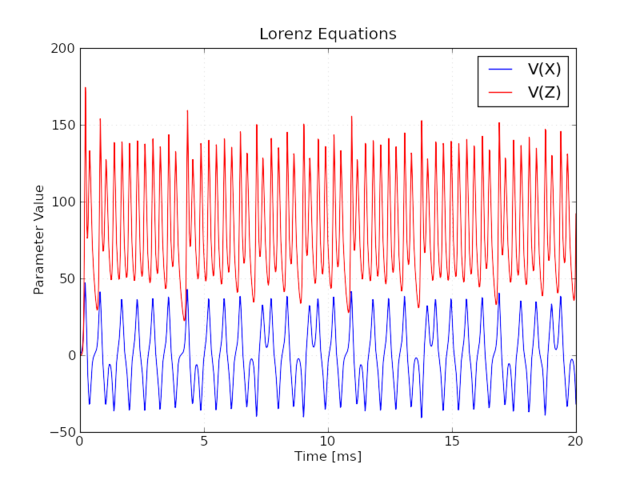
Výsledky simulácie Lorenzovej sústavy diferenciálnych rovníc sú uvedené pre hodnoty parametrov s=10, b=5, r=96.
Časový priebeh premenných x,z
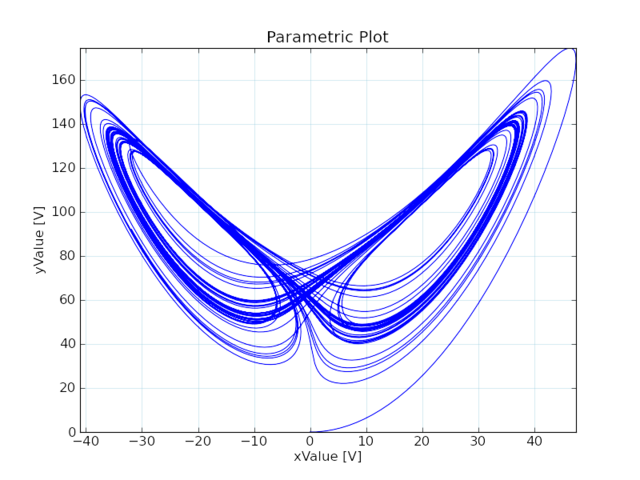
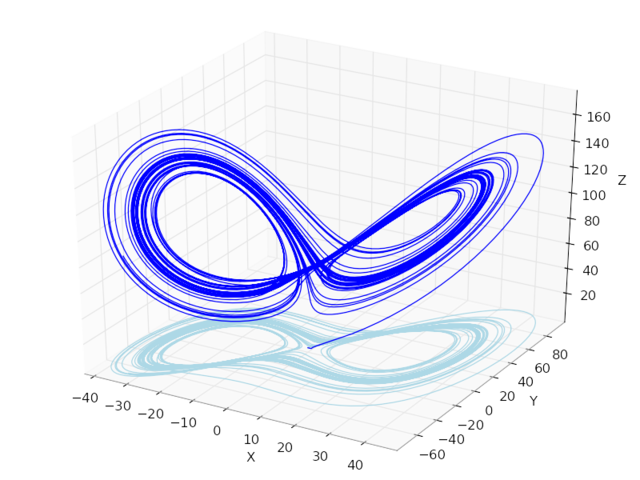
Parametrické 2D zobrazenie premenných x,z a 3D parametrické zobrazenie premenných x,y,z