A/D Prevodník s dvojnásobnou integráciou
1 Základná myšlienka
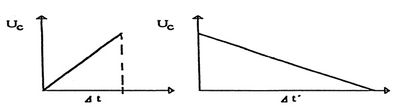
Základnú myšlienku, na ktorej je založená činnosť tohto typu prevodníka, si objasníme na obr. 1. Na ňom sú znázornené dva zdroje elektrického napätia. Napätie U jedného z nich poznáme. Je rovné napr. 10 V. Napätie druhého Umer nepoznáme a máme ho určiť meraním. Pri meraní budeme používať sústavu RC vytvorenú spojením rezistora s odporom R a kondenzátora s kapacitou C. Ak sa obidvoma vývodmi takej sústavy budeme dotýkať v priebehu určitej definovanej a relatívne krátkej doby Δt oboch pólov batérie s neznámym napätím, kondenzátor sa cez odpor R nabije na určité napätie, pričom počas nabíjania bude napätie na kondenzátore v čase lineárne narastať. Jeho priebeh vystihuje graf na obr. 2.
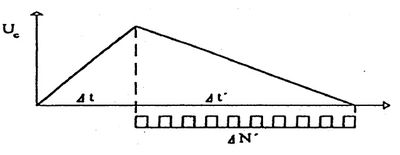
Po uplynutí definovanej doby Δt sústavu RC od zdroja napätia odpojíme. V meraní pokračujeme tak, že sústavu „RC” s nabitým kondenzátorom pripojíme teraz v znázornenej (opačnej) polarite k druhej batérii so známym napätím U. Kondenzátor sa teraz začne vybíjať a pri dlhodobejšom zapojení by sa začal eventuálne nabíjať aj na opačnú polaritu. Nás však zaujíma vybíjanie len do okamihu, kým sa kondenzátor celkom nevybije. Označme dobu úplného vybitia kondenzátora symbolom Δt'. Ak ju dokážeme zmerať, môžeme na jej základe určiť aj neznáme napätie aj Umer. Proces opísaného nabíjania a následného vybíjania kondenzátora spojeného s rezistorom možno vyniesť aj na graf. Graf vystihuje do istej miery aj spôsob merania vybíjacej doby Δt'. Tá sa určuje totiž na základe počítania impulzov, ktoré vyprodukuje za uvedenú dobu generátora impulzov. Tento počet je na grafe (obr. 3) označený ako ΔN'. Počítanie impulzov sa zastaví pritom v okamihu, keď napätie na kondenzátore dosiahne presne nulovú hodnotu.
3 Prečo sa uvažovaný prevodník nazýva prevodníkom s dvojitou integráciou?
V podstate preto, že RC obvod sa všeobecne využíva aj vo funkcii integrátora a to najmä v analógových počítačoch, ktoré boli kedysi v móde, no neskôr ustúpili rýchlym číslicovým počítačom. Faktom je, že napätie na kondenzátore, ktoré je priamo úmerné náboju na jeho doskách, je určené časovým integrálom pripojeného napätia na RC člen. Je teda
[math]UC = k∫Udt[/math]
kde k je konštanta. V našej situácii je však v oboch prípadoch pripojené napätie konštantné, takže integrálu sa dá ľahko „zbaviť”. Z posledného vzťahu získame závislosť U(t) pri nabíjaní v tvare
[math]Uc = k U Δt[/math]
Integrácia sa teda vybaví veľmi ľahko. Podobne je to jednoduché aj pri vybíjaní. Rozdiel je len v tom, že tam je zmenená polarita a tiež v tom, že sa vychádza zo začiatočného nabitého stavu kondenzátora.