Problém batoha: Rozdiel medzi revíziami
| Riadok 68: | Riadok 68: | ||
Program v jazyku C++: | Program v jazyku C++: | ||
| − | const n=3; | + | const n=3; |
| − | void greedy(double M,double W[n],double C[n],double X[n]) | + | void greedy(double M,double W[n],double C[n],double X[n]) |
| − | { double Z=M; | + | { double Z=M; |
| − | + | int i; | |
| − | + | for (i=0; i<n; i++) { | |
| − | + | if(W[i]>Z)a | |
| − | + | break; | |
| − | + | X[i]=1; | |
| − | + | Z=Z-W[i]; | |
| − | + | } | |
| − | if ((i<n)) | + | if ((i<n)) |
| − | X[i]=Z/W[i]; | + | X[i]=Z/W[i]; |
| − | } | + | } |
| − | int main() | + | int main() |
| − | { | + | { |
| − | + | double W[n]={10,12,16}, C[n]={60,70,80}, X[n]={0,0,0}; | |
| − | + | greedy(20,W,C,X); | |
| − | + | double p=0; | |
| − | + | for (int i=0 ;i<n; p+=X[i]*C[i],i++) | |
| − | + | cout<<i<<"\t"<<W[i]<<"\t"<<C[i]<<"\t"<<X[i]<<endl; | |
| − | + | cout<<"celkom:"<<p<<endl; | |
| − | + | system("pause"); } | |
Verzia zo dňa a času 17:31, 8. apríl 2010
Formulácia problému: Zlodej, ktorý vylomil zámok na trezore, zistil, že je naplnený n vecami rôznych veľkostí a rôznej ceny. Na lup má ale len batoh kapacity k, problém batohu je práve nájsť takú kombináciu vecí z trezoru, aby sa mu zmestila do batoha a bola čo možno najcennejšia.
Riešenie problému: Kľúčové pozorovanie, ktoré vedie k peknému riešeniu: Ak máme maximálne dosiahnuteľné ceny lupu pre všetky celočíselné kapacity batohu pomocou prvých k predmetov, ľahko spočítame maximálne ceny pre prvých k+1 predmetov. A to tak, že skúsime pridať k + 1 - vý predmet do batohu s k predmetmi a kapacitou nižšou o hmotnosť tohto predmetu. Predmet nepridáme, pokiaľ cena takého lupu nie je vyššia od ceny lupu z prvých k predmetov v batohu s rovnakou kapacitou. Prvý predmet je možné vložiť do batohu s kapacitou rovnou aspoň hmotnosti predmetu a cena lupu je maximálna možná. Pre ďalšie predmety to plynie z indukcie.
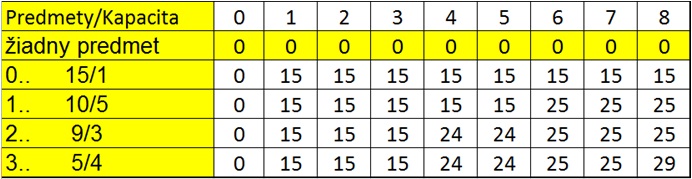
Vytvoríme tabuľku, kde stĺpce budú popisovať cieľovú nosnosť (kapacitu) batohu, posledný stĺpec bude maximálna nosnosť. Riadky budú označovať jednotlivé veci, ktoré môžeme do batohu vložiť. Budeme potrebovať n + 1 riadkov, kde n je počet predmetov. Riadok navyše máme pre žiadny vložený predmet. Ďalej budeme potrebovať k + 1 stĺpcov, jeden stĺpec navyše je pre kapacitu batoha o veľkosti 0.
Prvý stĺpec naplníme samými nulami, pretože to zodpovedá batohu s nulovou kapacitou. Prvý riadok je taktiež naplnený nulami, zodpovedá to totiž batohu so žiadnym vloženým predmetom. Tabuľku vypĺňame zľava doprava a zhora nadol. Do jednotlivých buniek vpisujeme hodnotu tak, že sa pozrieme na aktuálnu nosnosť batohu, potom na hmotnosť predmetu a jeho cenu a tiež sa musíme pozrieť na aktuálnu hodnotu vecí v batohu.
- V uvedenom príklade začíname s batohom so žiadnym vloženým predmetom. Tým pádom hodnota batohu je nulová.
Pokračujeme ďalej druhým riadkom postupne v smere rastúcej kapacity.
Celý riadok môžeme zaplniť touto hodnotou (riadiac sa podľa vzorca, ktorý je uvedený). - Prvý predmet má hmotnosť 1, teda sa vojde do batohu danej kapacity, čiže môžeme napísať, že cena takého batohu bude rovná cene predmetu. Konkrétne, keď sa pozrieme na prvý predmet a nosnosť batohu 6. Váha prvého predmetu je 5 a jeho cena 10. Zistíme, akú cenu mal batoh s rovnakou kapacitou, ale bez tohto predmetu a akú cenu by mal s kapacitou batohu nižšou o hmotnosť prvého predmetu s nultým predmetom a k tejto hodnote prirátame cenu prvého predmetu. - Vidíme, že druhá hodnota je väčšia, tým pádom napíšeme do bunky číslo 24. Takto postupne vypĺňame celú tabuľku. Výsledná hodnota je v pravom dolnom stĺpci.
Označme W={w1,w2,..wn} ako sadu hmotností a V={v1,v2,..vn} ako sadu hodnôt predmetov. Nech k je cieľová kapacita, predstavujúca najväčšiu hmotnosť vecí, ktorú batoh dokáže uniesť. Riešením problému je:
T. j. riešenie s maximálnou hodnotou a minimálnou váhou. Množina {0,1} indikuje, či predmet je v batohu alebo nie. Tento problém by sa dal riešiť rekurzívnou metódou. Táto metóda by bola ale veľmi neefektívna, lebo niektoré podproblémy by sa riešili viackrát.
Označme T[i][j] maximálnu cenu batohu s i predmetmi a nosnosťou o veľkosti j. Pri dynamickom programovaní teda využijeme tento vzorec:
ak j – váhy[i-1] < 0, potom T[i][j] =T [i - 1][j], inak T[i][j] = max (T[i-1,j], hodnoty[i-1] + T[i-1, j - váhy[i-1] ), pričom hodnoty je pole hodnôt jednotlivých predmetov a váhy je pole váh jednotlivých predmetov.
Iné prístupy k riešeniu:
Greedy algoritmus: tento prístup spočíva v tom, že keďže zlodej je veľmi chamtivý (greedy), tak berie predmety v klesajúcom poradí podľa ich ceny. Skončí s batohom, ktorý nie je úplne zaplnený. To, že batoh nie je úplne zaplnený ešte neznamená, že riešenie nie je správne, ale v mnohých prípadoch je to hlavnou príčinou.
Brute force: iný zlodej skúsil vypočítať všetky možnosti výberu vecí. Všetkých možností je ale 2n, takže zložitosť tohto algoritmu by bola exponenciálna.
Zložitosť algoritmu:
Časová zložitosť algoritmu závisí od veľkosti tabuľky.
Máme tu 2 faktory:
n + 1 riadkov, kde n je počet predmetov a
k + 1 stĺpcov, kde k je maximálna kapacita batohu.
Čiže časová zložitosť tohto algoritmu je O(k*n).
Číslo k ale nie je konštanta, môže byť oveľa väčšie ako počet vecí, ktoré môžeme do batohu vložiť.
Tento algoritmus má teda zložitosť rovnú pseudo – polynomiálnemu času.
Využitie:
Tento problém sa využíval ako základ pre kryptografický systém (ktorý bol odvtedy prelomený).
Ďalej sa využíva pri problémoch, kde riešenie závisí na výbere nejakého počtu vecí, ktorých hodnota je maximálna (alebo minimálna), a ktorých váha je rovná cieľovej váhe.
Program v jazyku C++:
const n=3;
void greedy(double M,double W[n],double C[n],double X[n])
{ double Z=M;
int i;
for (i=0; i<n; i++) {
if(W[i]>Z)a
break;
X[i]=1;
Z=Z-W[i];
}
if ((i<n))
X[i]=Z/W[i];
}
int main()
{
double W[n]={10,12,16}, C[n]={60,70,80}, X[n]={0,0,0};
greedy(20,W,C,X);
double p=0;
for (int i=0 ;i<n; p+=X[i]*C[i],i++)
cout<<i<<"\t"<<W[i]<<"\t"<<C[i]<<"\t"<<X[i]<<endl;
cout<<"celkom:"<<p<<endl;
system("pause"); }