Návrh a realizácia hydromodelovania vodných elektrární vážskej kaskády: Rozdiel medzi revíziami
(Vytvorená stránka „Kategória:Študentské práceKategória:Diplomové práce {{Hlavička_FM|{{PAGENAME}}|Bc. Rastislav Bohuš| Ing., Tomáš Páleník| 2009/2010 |Diplomový projekt …“) |
|||
| Riadok 127: | Riadok 127: | ||
y – hĺbka vody. | y – hĺbka vody. | ||
| − | <math> | + | {{vzorec|<math>S=\left( b+m\cdot y \right)y=\left( \beta +m \right){{y}^{2}}</math>|1.10}} |
| − | S=\left( b+m\cdot y \right)y=\left( \beta +m \right){{y}^{2}} | ||
| − | </math> | ||
| − | <math> | + | {{vzorec|<math> |
O=b+2y\sqrt{1+{{m}^{2}}}=b+{{m}_{0}}\cdot y=\left( \beta +{{m}_{0}} \right)y | O=b+2y\sqrt{1+{{m}^{2}}}=b+{{m}_{0}}\cdot y=\left( \beta +{{m}_{0}} \right)y | ||
| − | </math> | + | </math> |1.11}} |
| − | <math> | + | {{vzorec|<math> |
R=\frac{\left( b+m\cdot y \right)y}{b+2y\sqrt{1+{{m}^{2}}}}=\frac{\beta +m}{\beta +{{m}_{0}}}y | R=\frac{\left( b+m\cdot y \right)y}{b+2y\sqrt{1+{{m}^{2}}}}=\frac{\beta +m}{\beta +{{m}_{0}}}y | ||
| − | </math> | + | </math>|1.12}} |
| + | {{vzorec| | ||
<math> | <math> | ||
B=b+2m\cdot y=\left( \beta +2m \right)y | B=b+2m\cdot y=\left( \beta +2m \right)y | ||
| − | </math> | + | </math> |1.13}} |
kde | kde | ||
Verzia zo dňa a času 13:37, 6. apríl 2010

|
Trenčianska Univerzita Alexandra Dubčeka v Trenčíne
Fakulta Mechatroniky |

|
Návrh a realizácia hydromodelovania vodných elektrární vážskej kaskády zadanie práce Diplomový projekt |
| Autor: | Bc. Rastislav Bohuš |
| Pedagogický vedúci: |
Ing., Tomáš Páleník |
| Študijný odbor: | Mechatronika
|
| Akademický rok |
2009/2010
|
| 1. | Základné teoretické rovnice prúdenia v otvorených korytách |
| 2. | Hydromodelovanie vážskej kaskády
|
Obsah
| Abstrakt
slovensky |
| Abstract
anglicky |
Úvod Jednou z mnohých úloh, ktoré sú spracovávané na hydroenergetickom dispečingu v Trenčíne je modelovanie a plánovanie výroby na vodných elektrárňach takmer celého Slovenska. Plánovanie a riadenie výrobných zdrojov je veľmi náročné a preto sa pri riešení tejto úlohy využíva programový nástroj nazývaný hydromodel prípravy prevádzky, ktorého úlohou je umožniť pracovníkom prípravy hľadať reálne a zároveň optimálne riešenie nasadzovania výrobných zdrojov. Hlavnými vstupujúcimi parametrami do hydromodelu sú hladiny nádrží a prietokové množstvá vody. Turbogenerátory premieňajú potenciál vody na elektrický výkon a energia ktorá je vyrobená je zároveň v reálnom čase aj odberateľmi spotrebovaná. Preto celé riadenie ES vychádza zo zásady rešpektovania optimálneho riadenia jednotlivých subsystémov, medzi ktoré patrí aj hydroenergetický systém vážskej kaskády. Pre vážsku kaskádu to znamená optimálne využite hydropotenciálu na jednotlivých medzipovodiach pre pokrytie diagramu denného zaťaženia pri dodržaní všetkých okrajových vodohospodárskych a energetických podmienok. Hydromodelovaním je možné bezpečne a včasne vyhodnotiť výrobu a ostatnú situáciu počas bežnej prevádzky, povodňových stavov i počas hladinových a prietokových režimov, ktoré vyžadujú externé organizácie prípadne interné prevádzkarne a oddelenia SE-VE. Na tieto obmedzenia je potom možné reagovať s dostatočným časovým predstihom (nákup energii zo zahraničia, naplánovaním väčšej výroby na inom zdroji v rámci SE, dočasným zrušením hladinových alebo prietokových obmedzení atď.,).
Hydromodel, ktorý je prevádzkovaný na HED má svoje obmedzenia v metódach a prístupoch, ktoré by som chcel v tejto práci popísať a vyriešiť. Napriek tomu, že bol vytvorený s vedeckým prístupom a naprogramovaný v modernom vizualizačnom nástroji atď., práca s ním je ťažkopádna a oddelenie plánovania musí robiť iné kontroly na overenie správnosti vypočítaných výsledkov. Ďalším dôvodom je čas modelovania, ktorý pre jeden výpočet predstavuje v niektorých prípadoch aj hodinu, napriek rýchlemu výpočtu hydromodelu, ktorý je približne 20 až 30 sekúnd. Mnohé chyby generované modelom vznikli jeho zjednodušením do takej miery, že zlepšovanie naráža na technické aj ekonomické bariéry, muselo by dôjsť v niektorých prístupoch k celkovej zmene a k jeho celkovému preprogramovaniu.
V tejto práci budeme rozoberať jednotlivé metódy a prístupy pre nový hydromodel a jeho celkové programové vytvorenie. Budeme sa opierať o metódy z pôvodného hydromodelu a v niektorých prípadoch použijeme vhodnejšie metódy a prístupy, ktoré odbúrajú časovú náročnosť modelovania a výsledky zaťažené chybami.
Základné teoretické rovnice prúdenia v otvorených korytách
Teoretické rovnice prúdenia v otvorených korytách
Všeobecne možno prúdenie kvapalín rozdeliť na:
- neustále (nestacionárne), pri ktorom hydraulické veličiny závisia od polohy a času,
- ustálené (stacionárne), pri ktorom sa hydraulické veličiny s časom nemenia, sú iba funkciou polohy. Ustálené prúdenie môže byť nerovnomerné s premennými veličinami a rovnomerné s konštantnou rýchlosťou prúdenia.
Podľa spôsobu vedenia prúdu kvapaliny rozoznávame:
- tlakové prúdenie, ktoré sa vyskytuje v potrubiach,
- beztlakové prúdenie, ktoré sa vyskytuje v umelých kanáloch , otvorených korytách.
Podľa tvaru prietokového profilu rozdeľujeme otvorené korytá na:
- prizmatické kanály s konštantnými geometrickými vlastnosťami po dĺžke toku,
- neprizmatické kanály s premenným tvarom po dĺžke, pričom zmeny priečneho tvaru profilu možno matematicky definovať ako funkcie prietokovej plochy (omočeného obvodu),
- prirodzené korytá s nepravidelným tvarom prietokového profilu, meniacim sa po dĺžke toku.
Prierezy kanálov a korýt sú:
- jednoduché
- zložené skladajúce sa z jednotlivých častí prietokového profilu s odlišnými kvantitatívnymi vlastnosťami prúdenia.
Definovanie základných geometrických a hydraulických charakteristík:
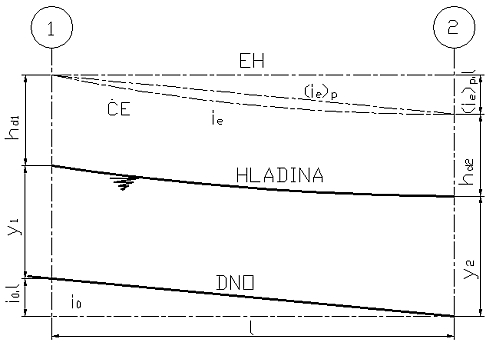
Prietokový profil je rovinný rez pevným vedením prúdu, kolmý na jeho pozdĺžnu os a charakterizujúci jeho tvar (obdĺžnikový, lichobežníkový, kruhový profil). Prúdiaca kvapalina vypĺňa, resp. môže vypĺňať celý prietokový profil alebo jeho časť (Obr. 1.1).
Prietoková plocha S je plošný obsah rezu prúdu plochou kolmou v každom bode na vektor bodovej rýchlosti. V praktických prípadoch sa zjednodušuje na plošný obsah rovinného rezu, vedeného kolmo na strednú prúdnicu, ktorá charakterizuje celkový smer prúdenia. Omočený obvod O je dĺžka časti obvodu prietokového profilu, na ktorej je voda v styku s pevným vedením. Hydraulický polomer R je definovaný ako podiel prietokovej plochy k omočenému obvodu.
[math] R=\frac{S}{O} [/math] (1.1)
Ustálené prúdenie: Ustálené plynulé sa meniace prúdenie v otvorených korytách je pre konštantný prietok v toku opísané diferenciálnou rovnicou
[math] \frac{dy}{dl}=\frac{{{i}_{0}}-\frac{{{Q}^{2}}}{{{C}^{2}}\cdot {{S}^{2}}\cdot R}+\frac{\alpha \cdot {{Q}^{2}}}{g\cdot {{S}^{3}}}\cdot \frac{\partial S}{\partial b}\cdot \frac{\partial b}{\partial l}}{1-\frac{\alpha \cdot {{Q}^{3}}\cdot B}{g\cdot {{S}^{3}}}} [/math] (1.2)
kde:
- Q – prietok;
- C – rýchlostný súčiniteľ (Chézyho súčiniteľ);
- b – premenná vyjadrujúca šírku toku v závislosti od hĺbky vody v koryte y;
- B – šírka koryta v hladine.
Rovnica (1.2) vyplýva z Bernoulliho rovnice pre dva prierezy vzdialené na dĺžke dl. Pre prizmatické korytá sa rovnica zjednoduší na tvar
[math] \frac{dy}{dl}=\frac{{{i}_{0}}-\frac{{{Q}^{2}}}{{{C}^{2}}\cdot {{S}^{2}}\cdot R}}{1-\frac{\alpha \cdot {{Q}^{2}}\cdot B}{g\cdot {{S}^{3}}}} [/math] (1.3)
Po zavedení modulu prietoku K definovaného výrazom [math] K=C\cdot S\sqrt{R} [/math] (1.4)
a bezrozmerného Froudovho čísla Fr
[math]
Fr=\frac{v}{\sqrt{g\cdot l}}\sqrt{\frac{\alpha \cdot B}{g\cdot S}}\cdot \frac{Q}{S}
[/math] (1.5)
môžeme rovnicu pre prizmatické korytá zjednodušiť na tvar
[math] \frac{dy}{dl}=\frac{1-{{\left( \frac{{{K}_{0}}}{K} \right)}^{2}}}{1-F{{r}^{2}}}{{i}_{0}} [/math] (1.6)
Pre rovnomerné prúdenie platí Q = konštanta, v = konštanta => S = konštanta => y = konštanta
Tieto podmienky platné pre prizmatické korytá budú splnené vtedy, keď sklon hladiny bude rovnaký ako sklon dna a čiary energie
[math] {{i}_{0}}=i={{i}_{e}} [/math] (1.7)
Z tejto rovnosti vyplýva, že hĺbka sa nemení po dĺžke
[math] \frac{dy}{dl}=0 [/math] (1.8)
a rovnica (1.3) dostane tvar
[math] Q=C\cdot S\sqrt{R\cdot {{i}_{0}}} [/math] (1.9)
je to Chézyho rovnica pre rovnomerné prúdenie v otvorených korytách. Rovnomerné prúdenie môže vzniknúť len vtedy, keď všetky charakteristiky koryta zostávajú po celej dĺžke konštantné. Koryto musí byť prizmatické, pokiaľ ide o tvar priečneho profilu, musí mať však konštantný sklon dna a nemennú drsnosť v závislosti od dĺžky. V prírodných podmienkach sa s rovnomerným ustáleným prúdením stretávame málokedy. Z hľadiska riešenia úloh je však jednoduchý a preto si s ním pomáhame pri riešení komplikovaných úloh.
Prúdenie v kanáloch a otvorených korytách
V tejto časti sa budeme zaoberať riešením úlohy pre prizmatické kanály, a to výhradne pre rovnomerné ustálené prúdenie. Opíšeme v nich základné geometrické, drsnostné a hydraulické charakteristiky kanálov.
Charakteristiky prizmatických kanálov
Geometrické charakteristiky - veličiny charakterizujúce geometriu prietokového profilu prizmatických kanálov sú:
- rozmery prietokového profilu (šírka v dne, sklon svahov, priemer a pod.);
- prietoková plocha (prietokový prierez) S [m2];
- omočený obvod O [m];
- hydraulický polomer R [m];
- šírka v hladine B [m].
Pre tvar lichobežníkového prietokového profilu sú predchádzajúce parametre opísané podľa vzťahov:
b – šírka v dne kanála;
1:m – sklon svahov;
y – hĺbka vody.
|
[math]S=\left( b+m\cdot y \right)y=\left( \beta +m \right){{y}^{2}}[/math] |
(1.10) |
|
[math] O=b+2y\sqrt{1+{{m}^{2}}}=b+{{m}_{0}}\cdot y=\left( \beta +{{m}_{0}} \right)y [/math] |
(1.11) |
|
[math] R=\frac{\left( b+m\cdot y \right)y}{b+2y\sqrt{1+{{m}^{2}}}}=\frac{\beta +m}{\beta +{{m}_{0}}}y [/math] |
(1.12) |
|
[math] B=b+2m\cdot y=\left( \beta +2m \right)y [/math] |
(1.13) |
kde
[math] \begin{align} & \beta =\frac{b}{y} \\ & {{m}_{0}}=2\sqrt{1+{{m}^{2}}} \\ \end{align} [/math]
Hydraulické charakteristiky – veličiny charakterizujúce prúdenie a drsnostné podmienky podmieňujúce prúdenie sú:
- stupeň drsnosti n;
- rýchlostný súčiniteľ (Chézyho súčiniteľ) C [m0,5.s-1];
- prietok Q [[math]m^3 * s^{-1} [/math]].
Pre prizmatické prierezy kanálov určíme uvedené charakteristiky následovne: Stupeň drsnosti je veličina na určenie rýchlostného súčiniteľa, ktorá sa vyskytuje takmer vo všetkých vzťahoch. Stupne drsnosti poznáme podľa Manninga n a podľa Agroskina [math]k_A[/math], pričom ich vzájomný vzťah je
[math] {{k}_{A}}=\frac{0,05643}{n} [/math]
vlozit tabulku 1
Stupeň drsnosti pre dané pomery (druh opevnenia, povrch omočeného obvodu, jeho stav), pričom táto veličina je premenná v čase, nielen pre narušenie opevnenia, ale aj počas roka (porast svahov korýt a pod.). Pri výbere stupňa drsnosti treba postupovať zodpovedne a treba využívať predovšetkým praktické skúsenosti.
Rýchlostný súčiniteľ je hodnota vystupujúca v Chézyho vzťahu na výpočet strednej prierezovej rýchlosti v alebo Q. Aj v súčasnosti sa určuje pomocou mnohých empirických vzťahov napr. Pavlovského vzťah s hranicami platnosti 0,1 m < R < 3,0 m.
[math] C=\frac{1}{n}{{R}^{y}},\ kde\,\,y=2,5\sqrt{n}-0,13-0,75R\left( \sqrt{n}-0,10 \right) [/math] (1.15)
Hodnoty v rozsahu 0,1m až 5,0m sú v tabuľke prílohy číslo XXX
Prietok Q počítame z Chézyho rovnice, pričom pri rovnomernom prúdení použijeme sklon dna koryta [math]i_0[/math]
[math] Q=C\cdot S\sqrt{R\cdot {{i}_{0}}}=K\sqrt{{{i}_{0}}} [/math] (1.16) a pri všeobecnom prípade rovnomerného prúdenia za sklon dosadíme sklon čiary energie [math]i_e[/math]
[math] Q = C \cdot S\sqrt {R \cdot {i_e}} = K\sqrt {{i_e}} [/math] (1.16)