Numerická integrácia Simpsonovou metódou (Python)

Numerické integrovanie Simpsonovou metódou využíva aproximáciu pôvodnej funkcie pomocou paraboly. Hodnotu funkcie f(x) nahradíme pre všetky body x z podintervalu <x_2k-1,x_2k+1> parabolou prechádzajúcou bodmi f(x_2k-1),f(x_2k),f(x_2k+1). f(x_2k-1)=Ah²-Bh+C f(x_2k)=C f(x_2k+1)=Ah²+Bh+C kde A,B,C sú neznáme parametre funkcie.

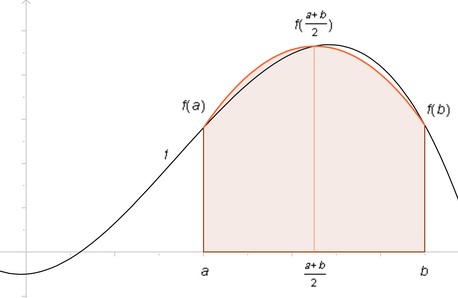
Integrovaný interval <a,b> pod parabolou je rozdelený na 2r intervalov s veľkosťou h=(b-a)/2r.

# Numerické integrovanie Simpsonovou metódou

# Simpsonova metóda spočíva v nahradení integrovanej funkcie parabolou prechádzajúcou troma bodmi

# na začiatku použivateľ zadá funkciu (sin(x),cos(x),tan(x),x^2,ln(x),exp(x))

# potom zadá interval, na ktorom sa má funkcia zintegrovať

# a nakoniec zadá presnosť, resp. krok, s akým ju chce zintegrovať



import math



print("Funkcie, ktoré môžete zadať, sú: sin(x),cos(x),tan(x),x^2,ln(x),exp(x)")

funkcia = input("Zadajte funkciu, pod ktorou chcete vypočítať obsah: ")

a = input("Zadajte spodnú hranicu intervalu, v ktorom chcete integrovať: ")

b = input("Zadajte hornú hranicu intervalu, v ktorom chcete integrovať: ")

krok = input("Zadajte krok, s ktorým chcete integrovať: ")



f=[]

x=float(a)

krok=float(krok)

a=float(a)

b=float(b)

i=0





if funkcia=="sin(x)":

    while x<=b:

        f.append(math.sin(x))

        x+=krok

        i+=1

elif funkcia=="cos(x)":

    while x<=b:

        f.append(math.cos(x))

        x+=krok

        i+=1

elif funkcia=="tan(x)":

    while x<=b:

        f.append(math.tan(x))

        x+=krok

        i+=1

elif funkcia=="x^2":

    while x<=b:

        f.append(math.pow(x,2))

        x+=krok

        i+=1

elif funkcia=="ln(x)":

    while x<=b:

        f.append(math.log(x))

        x+=krok

        i+=1

elif funkcia=="exp(x)":

    while x<=b:

        f.append(math.exp(x))

        x+=krok

        i+=1

else:

    print("fukcia bola zadaná nesprávne")



sum1=0

sum2=0

j=0



while j<i:

    if (j/2)>(int(j/2)): 

      sum1+=f[j]

    else:

      sum2+=f[j]

    j+=1

      

I=((b-a)/(3*i))*(f[0]+4*sum1+2*sum2)



print ("Vypočítaný obsah je: "+str(I))