Výpočet elektrického poľa metódou konečných diferencií: Rozdiel medzi revíziami
| Riadok 36: | Riadok 36: | ||
| − | + | Indexy priraďuje: | |
<source lang="python"> | <source lang="python"> | ||
| Riadok 43: | Riadok 43: | ||
return (i - 1)*(n - 1) + j - 1 | return (i - 1)*(n - 1) + j - 1 | ||
return (i - 1)*(n - 1) + j</source> | return (i - 1)*(n - 1) + j</source> | ||
| + | |||
| + | |||
| + | A maticu vypĺňa: | ||
| + | |||
| + | <source lang="python"> | ||
| + | matrix = [] | ||
| + | for i in xrange(m): | ||
| + | matrix.append([]) | ||
| + | for j in xrange(n): | ||
| + | if i == 0 or j == n - 1: | ||
| + | c = 1 | ||
| + | elif i == m - 1 and j == 0: | ||
| + | c = 0 | ||
| + | else: | ||
| + | c = "x" | ||
| + | matrix[i].append(c) | ||
| + | </source> | ||
| Riadok 135: | Riadok 152: | ||
for i in xrange(unknown): | for i in xrange(unknown): | ||
mama[i][i] = -4</source> | mama[i][i] = -4</source> | ||
| + | |||
| + | Maticu ktorú získame sa ešte upraví a vyrieši: | ||
| + | |||
| + | <source lang="python"> | ||
| + | results = [] | ||
| + | for i in xrange(unknown): | ||
| + | results.append(mama[i][-1]) | ||
| + | del mama[i][-1] | ||
| + | |||
| + | huhu = list(numpy.linalg.solve(mama, results))</source> | ||
| + | |||
| + | |||
| + | Ak chceme dostať číselné výsledky pre všetky zvolené body, môžeme dať vypísať maticu "matrix". | ||
| + | |||
| + | <source lang="python"> | ||
| + | for b in xrange(m): | ||
| + | for c in xrange(m): | ||
| + | if matrix[b][c] == "x": | ||
| + | matrix[b][c] = huhu[0] | ||
| + | del huhu[0]</source> | ||
| + | |||
| + | Ak však chceme výsledok graficky zobraziť ako ekvipotenciálne čiary, dá sa to spraviť tak, že budeme porovnávať jednotlivé zaokrúhlené výsledky s nejakými vybranými výsledkami. | ||
| + | |||
| + | <source lang="python"> | ||
| + | suradnicax = [] | ||
| + | suradnicay = [] | ||
| + | #suradnicax2 = [] | ||
| + | #suradnicay2 = [] | ||
| + | for x in xrange(m): | ||
| + | for y in xrange(m): | ||
| + | if matrix[x][y] == matrix [0][m/2]: | ||
| + | #print matrix[x][y] | ||
| + | uloz_suradnice(x,y) | ||
| + | lobogo += 4 | ||
| + | elif round(matrix[x][y],3) == round(matrix [-1][2*m/3],3): | ||
| + | uloz_suradnice(x,y) | ||
| + | lobogo += 4 | ||
| + | elif round(matrix[x][y],3) == round(matrix [-1][5*m/6],3): | ||
| + | uloz_suradnice(x,y) | ||
| + | lobogo += 4 | ||
| + | elif round(matrix[x][y],3) == round(matrix [-1][m/3],3): | ||
| + | uloz_suradnice(x,y) | ||
| + | lobogo += 4 | ||
| + | elif round(matrix[x][y],3) == round(matrix [-1][14*m/15],3): | ||
| + | uloz_suradnice(x,y) | ||
| + | lobogo += 4 | ||
| + | elif round(matrix[x][y],3) == round(matrix [-1][25*m/26],3): | ||
| + | uloz_suradnice(x,y) | ||
| + | lobogo += 4 | ||
| + | elif round(matrix[x][y],3) == round(matrix [-1][m/6],3): | ||
| + | uloz_suradnice(x,y) | ||
| + | lobogo += 4</source> | ||
| + | |||
| + | |||
| + | Vykreslenie takýchto výsledkov sa dá uskutočniť ako "scatter". | ||
| + | |||
| + | <source lang="python"> | ||
| + | for a in xrange(lobogo): | ||
| + | matplotlib.pyplot.scatter(suradnicax[a], suradnicay[a], s=20, c='b', marker='o', cmap=None, norm=None, | ||
| + | vmin=None, vmax=None, alpha=1.0, linewidths=None, | ||
| + | verts=None,) | ||
| + | show() </source> | ||
Verzia zo dňa a času 10:56, 15. jún 2011
Tento program som napísal ako projekt ku predmetu Pokročilé programovanie na FMFI UK. Úloha ktorú som si stanovil, bola použitie metódy konečných diferencii na vypočítanie priebehu elektrického poľa.
Metóda konečných diferencii je jednoduchá numerická metóda, ktorá spočíva v diskretizovaní zadanej úlohy a jej riešení v jednotlivých strategicky zvolených bodoch. V našom prípade diskretizujeme riešenie dvojrozmernej Poissonovej rovnice na výpočet elektrického poľa.
Tá má tvar: [math]\frac{\partial^{2} U}{\partial x^2} + \frac{\partial^{2} U}{\partial y^{2}} = - \frac{Q}{\kappa} [/math]
Zvolíme si vhodné rozloženie bodov na diskretizáciu. Vhodným rozložením na riešenie „hranatej“ úlohy, je pravouhlá mriežka.
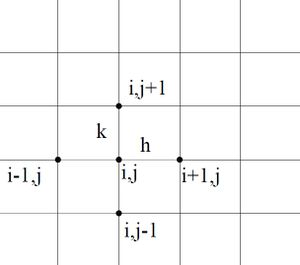
Aproximácia problému touto metódou spočíva v nahradení derivácii v jednotlivých bodoch siete diferenciáciou. Potom je hľadaná veličina v bode vypočítaná z hodnôt veličiny v okolitých bodoch. Hodnota potenciálu v bode i, j sa vyjadrí podľa hodnôt v bodoch x+h a x-h (analogicky tiež y+k, y-k) , ktoré sa rozvinú do Taylorovho radu. Úpravami týchto rozvojov dostaneme vyjadrenie druhej derivácie potenciálu v bode i,j v závislosti od hodnôt potenciálu vedľajších bodov v x-ovom alebo y-ovom smere a od hodnoty v bode i,j.
Dostaneme: [math]U''_{i,j}=\frac{U_{i+1,j}-2U_{i,j}+U_{i-1,j}}{h^{2}}[/math] a [math]U''_{i,j}=\frac{U_{i,j+1}-2U_{i,j}+U_{i,j-1}}{k^{2}}[/math]
Tieto rovnice sú aproximáciou druhých parciálnych derivácii potenciálov podľa x a y. Boli však vyjadrené zanedbaním členov Taylorovho rozvoja s mocninou 3 a viac. Chyba aproximácie bude teda rádu h2 resp. k2.
Dostali sme teda: [math]\frac{\partial^{2}U}{\partial x^2} = \frac{U_{i+1,j}-2U_{i,j}+U_{i-1,j}}{h^{2}}[/math] a [math]\frac{\partial^{2}U}{\partial y^2} = \frac{U_{i,j+1}-2U_{i,j}+U_{i,j-1}}{k^{2}}[/math]
Po doplnení do základnej rovnice: [math]\frac{1}{h^{2}}({U_{i+1,j}-2U_{i,j}+U_{i-1,j}}) + \frac{1}{k^{2}}({U_{i,j+1}-2U_{i,j}+U_{i,j-1}}) + Q = 0[/math]
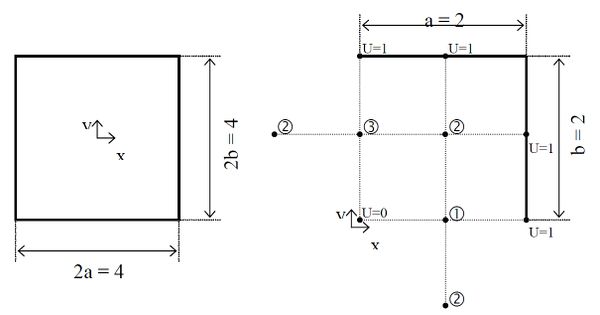
Samotná úloha pozostáva zo zistenia priebehu potenciálu vnútri prierezu štvorcového koaxiálneho vodiča. Vnútorný vodič môže mať potenciál rovný 0. Potenciál na vonkajšom plášti môžeme pre jednoduchosť nahradiť 100% čiže 1.
V závislosti od požadovanej presnosti výpočtu rozdelíme vnútro jedného kvadrantu vodiča (úloha je symetrická) na indexované body. Indexy priradíme iba bodom ktoré majú neznámy potenciál.
Indexy priraďuje:
def get_index(i, j, m, n):
if i == m - 1:
return (i - 1)*(n - 1) + j - 1
return (i - 1)*(n - 1) + j
A maticu vypĺňa:
matrix = []
for i in xrange(m):
matrix.append([])
for j in xrange(n):
if i == 0 or j == n - 1:
c = 1
elif i == m - 1 and j == 0:
c = 0
else:
c = "x"
matrix[i].append(c)
Aplikovaním poslednej rovnice na tieto body dostaneme sústavu troch rovníc.
[math](0-2U_{1}+1)+(U_{2}-2U_{1}+U_{2})=0[/math]
[math](U_{3}-2U_{2}+1)+(U_{1}-2U_{2}+1)=0[/math]
[math](U_{2}-2U_{3}+U_{2})+(0-2U_{3}+1)=0[/math]
Vhodným zvolením rozmerov oblasti sme eliminovali h a k.
Ak požadujeme väčšiu presnosť, budeme musieť oblasť rozdeliť na viac bodov a následne budeme riešiť viac rovníc.
Túto sústavu napíšeme v maticovom tvare:
[math]
\begin{pmatrix}
-4 & 2 & 0 \\
1 & -4 & 1 \\
0 & 2 & -4 \\
\end{pmatrix}
\begin{pmatrix}
U_1 \\
U_2 \\
U_3 \\
\end{pmatrix} =
\begin{pmatrix}
-1 \\
-2 \\
-1 \\
\end{pmatrix}[/math]
Po vyriešení tejto sústavy lineárnych rovníc dostaneme hodnoty potenciálov v troch bodoch U1, U2 a U3.
Všetky tieto kroky sa v programe vykonávajú už akoby "v matici". Podľa polohy riešeného bodu v mriežke rozdeľujúcej kvadrant koaxiálneho vodiča sa do matice dosádzajú čísla. Týchto čísel je iba obmedzený počet. Sú to: 0, 1, 2, -4 a 0, 1, 2 vo výsledkovej časti.
mama = []
for i in xrange(m):
for j in xrange(n):
if matrix[i][j] == "x":
row = []
for _ in xrange(unknown + 1):
row.append(0)
#lavy kraj
if j == 0:
row[get_index(i, j + 1, m, n)] = 2
if i - 1 == 0:
row[-1] = -1
else:
row[get_index(i - 1, j, m, n)] = 1
if not i == m - 2:
row[get_index(i + 1, j, m, n)] = 1
#pravy kraj
elif j == n - 2:
if not (i == m - 1 and j == 1):
row[get_index(i, j - 1, m, n)] = 1
row[-1] = -1
if i == 1:
row[-1] = -2
else:
if i == m - 1:
row[get_index(i - 1, j, m, n)] = 2
else:
row[get_index(i - 1, j, m, n)] = 1
if not i == m - 1:
row[get_index(i + 1, j, m, n)] = 1
#hore
elif i == 1:
row[get_index(i + 1, j, m, n)] = 1
row[get_index(i, j - 1, m, n)] = 1
row[get_index(i, j + 1, m, n)] = 1
row[-1] = -1
#dole
elif i == m - 1:
if j != 1:
row[get_index(i, j - 1, m, n)] = 1
row[get_index(i - 1, j, m, n)] = 2
row[get_index(i, j+1, m, n)] = 1
else:
row[get_index(i, j+1, m, n)] = 1
row[get_index(i, j-1, m, n)] = 1
row[get_index(i + 1, j, m, n)] = 1
row[get_index(i - 1, j, m, n)] = 1
mama.append(row)
for i in xrange(unknown):
mama[i][i] = -4
Maticu ktorú získame sa ešte upraví a vyrieši:
results = []
for i in xrange(unknown):
results.append(mama[i][-1])
del mama[i][-1]
huhu = list(numpy.linalg.solve(mama, results))
Ak chceme dostať číselné výsledky pre všetky zvolené body, môžeme dať vypísať maticu "matrix".
for b in xrange(m):
for c in xrange(m):
if matrix[b][c] == "x":
matrix[b][c] = huhu[0]
del huhu[0]
Ak však chceme výsledok graficky zobraziť ako ekvipotenciálne čiary, dá sa to spraviť tak, že budeme porovnávať jednotlivé zaokrúhlené výsledky s nejakými vybranými výsledkami.
suradnicax = []
suradnicay = []
#suradnicax2 = []
#suradnicay2 = []
for x in xrange(m):
for y in xrange(m):
if matrix[x][y] == matrix [0][m/2]:
#print matrix[x][y]
uloz_suradnice(x,y)
lobogo += 4
elif round(matrix[x][y],3) == round(matrix [-1][2*m/3],3):
uloz_suradnice(x,y)
lobogo += 4
elif round(matrix[x][y],3) == round(matrix [-1][5*m/6],3):
uloz_suradnice(x,y)
lobogo += 4
elif round(matrix[x][y],3) == round(matrix [-1][m/3],3):
uloz_suradnice(x,y)
lobogo += 4
elif round(matrix[x][y],3) == round(matrix [-1][14*m/15],3):
uloz_suradnice(x,y)
lobogo += 4
elif round(matrix[x][y],3) == round(matrix [-1][25*m/26],3):
uloz_suradnice(x,y)
lobogo += 4
elif round(matrix[x][y],3) == round(matrix [-1][m/6],3):
uloz_suradnice(x,y)
lobogo += 4
Vykreslenie takýchto výsledkov sa dá uskutočniť ako "scatter".
for a in xrange(lobogo):
matplotlib.pyplot.scatter(suradnicax[a], suradnicay[a], s=20, c='b', marker='o', cmap=None, norm=None,
vmin=None, vmax=None, alpha=1.0, linewidths=None,
verts=None,)
show()