Kmity sústavy s dvoma stupňami volnosti: Rozdiel medzi revíziami
| Riadok 59: | Riadok 59: | ||
Túto rovnicu nazývame charakteristickou rovnicou systému. Vo všeobecnosti má dva korene <math>\omega_1^2</math> a <math>\omega_2^2</math>. | Túto rovnicu nazývame charakteristickou rovnicou systému. Vo všeobecnosti má dva korene <math>\omega_1^2</math> a <math>\omega_2^2</math>. | ||
| + | |||
| + | === Výpočet sústavy === | ||
| + | |||
| + | V interaktívnom móde Pythonu (konzola, iPython<ref>http://ipython.github.com/ipython-doc/</ref>) importujeme balík ''pylab'' pre vedecké výpočty | ||
| + | <source lang="python"> | ||
| + | >>> from pylab import * | ||
| + | </source> | ||
| + | |||
| + | |||
| + | === Literatúra a odkazy === | ||
| + | <references/> | ||
Verzia zo dňa a času 19:40, 18. marec 2011
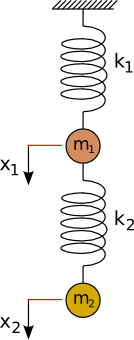
Na obrázku je zobrazená sústava dvoch telies a dvoch pružín. Prvá pružina je pevne ukotvená, hmotnosti telies sú m1 a m2, ich výchylky z rovnovážnej polohy sú x1 a x2. V zobrazenej pozícii je sústava v rovnováhe, pružiny sú natiahnuté pôsobením vlastnej hmotnosti telies, do pohybových rovníc preto nebudeme zahŕňať tiažové sily m1g a m2g.
Pri vychýlení z rovnovážnej polohy pôsobia na telesá sily úmerné ich výchylkám z rovnovážnych polôh a konštantám pružín k1 a k2. Pre obe telesá môžeme potom napísať pohybové rovnice
- [math] m_1 \ddot{x_1}=-k_1 x_1 + k_2(x_2-x_1) [/math]
- [math] m_2 \ddot{x_2}=-k_2(x_2-x_1) [/math]
Analýza sústavy
Pri analýze sústavy predpokladáme, že pohyb telies bude harmonický s rovnakou frekvenciou a môžeme ho preto popísať vzťahmi
- [math] x_1 =A_1 sin(\omega t)\, [/math]
- [math] x_2 =A_2 sin(\omega t)\, [/math]
Hľadanou veličinou je frekvencia kmitov telies. Dosadením do pohybových rovníc dostaneme
- [math] -m_1 A_1\, \omega^2 + (k_1 + k_2)A_1 - k_2 A_2 = 0\, [/math]
- [math] -m_2 A_2\, \omega^2 - k_2 A_1 + k_2 A_2 = 0\, [/math]
Úpravou dostaneme maticový zápis sústavy pohybových rovníc
- [math] \left[ \begin{array}{cc} {[(k_1+k_2)-m_1 \omega^2]} & -k_2 \\ -k_2 & {[k_2-m_2 \omega^2]} \end{array} \right] \left[ \begin{array}{c} A_1 \\ A_2 \end{array} \right] = 0 [/math]
Homogénna sústava rovníc má netriviálne riešenie len vtedy, ak determinant sústavy je rovný nule, z toho vyplýva
- [math] \omega^4 - \left[ \frac{k_1+k_2} {m_1} + \frac{k_2}{m_2} \right] \omega^2 + \frac{k_1}{m_1} \frac{k_2}{m_2}=0 [/math]
Túto rovnicu nazývame charakteristickou rovnicou systému. Vo všeobecnosti má dva korene [math]\omega_1^2[/math] a [math]\omega_2^2[/math].
Výpočet sústavy
V interaktívnom móde Pythonu (konzola, iPython[1]) importujeme balík pylab pre vedecké výpočty
>>> from pylab import *