Riešenie obvodov metódou slučkových prúdov: Rozdiel medzi revíziami
Skočit na navigaci
Skočit na vyhledávání
(Vytvorená stránka „__NOTOC__ Category:Python Maticové metódy rozširujúceho balíka Pythonu ''pylab''<ref>http://www.scipy.org/PyLab</ref> je možné použiť pre analýzu jednoduchej…“) |
|||
| Riadok 7: | Riadok 7: | ||
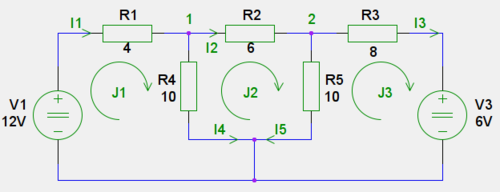
Analyzovaný obvod pozostáva z rezistorov a napäťových zdrojov. V obvode sú vyznačené slučkové prúdy J1, J2 a J3. | Analyzovaný obvod pozostáva z rezistorov a napäťových zdrojov. V obvode sú vyznačené slučkové prúdy J1, J2 a J3. | ||
| − | [[Súbor:py-cc-sch.png | thumb|center| | + | [[Súbor:py-cc-sch.png | thumb|center|500px | <div align="center"> Zapojenie obvodu </div>]] |
Pre slučku J1 môžeme na základe druhého Kirchhofovho zákona písať | Pre slučku J1 môžeme na základe druhého Kirchhofovho zákona písať | ||
| Riadok 27: | Riadok 27: | ||
</math> | </math> | ||
| + | Prepisom do maticového tvaru dostaneme | ||
| + | |||
| + | :<math> | ||
| + | \left[ \begin{array}{ccc} | ||
| + | {R1+R4} & -R4 & 0 \\ | ||
| + | -R4 & {R2+R4+R5} & -R5 \\ | ||
| + | 0 & -R5 & {R3+R5} \end{array} \right] | ||
| + | \left[ \begin{array}{c} | ||
| + | J1 \\ | ||
| + | J2 \\ | ||
| + | J3 \end{array} \right] | ||
| + | = | ||
| + | \left[ \begin{array}{c} | ||
| + | V1 \\ | ||
| + | 0 \\ | ||
| + | -V3 \end{array} \right] | ||
| + | </math> | ||
=== Literatúra a odkazy === | === Literatúra a odkazy === | ||
<references/> | <references/> | ||
Verzia zo dňa a času 21:00, 16. marec 2011
Maticové metódy rozširujúceho balíka Pythonu pylab[1] je možné použiť pre analýzu jednoduchej elektrickej siete metódou slučkových prúdov.
Analýza obvodu
Analyzovaný obvod pozostáva z rezistorov a napäťových zdrojov. V obvode sú vyznačené slučkové prúdy J1, J2 a J3.
Pre slučku J1 môžeme na základe druhého Kirchhofovho zákona písať
- [math] R1 J1 + R4 (J1-J2)=V1 \, [/math]
pre slučku J2
- [math] R2 J2 + R5 (J2-J3) + R4(J2-J1) = 0 \, [/math]
a pre slučku J3
- [math] -R5 J2 + (R3+R5)J3 = -V3 \, [/math]
Prepisom do maticového tvaru dostaneme
- [math] \left[ \begin{array}{ccc} {R1+R4} & -R4 & 0 \\ -R4 & {R2+R4+R5} & -R5 \\ 0 & -R5 & {R3+R5} \end{array} \right] \left[ \begin{array}{c} J1 \\ J2 \\ J3 \end{array} \right] = \left[ \begin{array}{c} V1 \\ 0 \\ -V3 \end{array} \right] [/math]