Opis modelovaného systému a jednotlivých častí hydromodelu: Rozdiel medzi revíziami
| Riadok 668: | Riadok 668: | ||
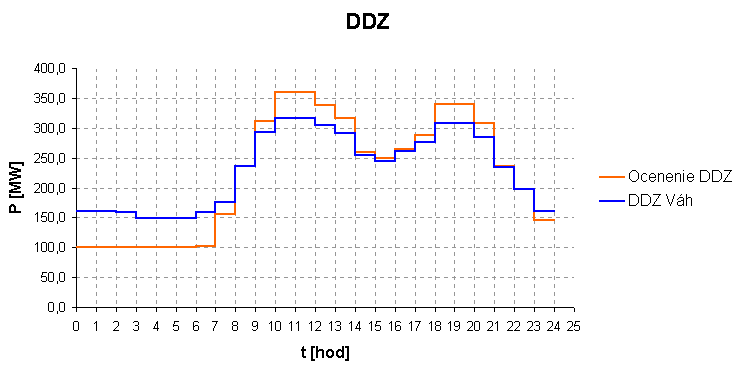
Ocenenie DDZ - Tento vstupný parameter vyjadruje výrobu v MWh a hodnotu veľkosti nasadenia v MW pre každú hodinu dňa. Takýmto spôsobom sú určené váhové hodnoty jednotlivých hodín, ktoré vyjadrujú veľkosť nasadenia energetických zariadení do prevádzky. Optimalizačný model v závislosti od ostatných vstupných podmienok navrhne nasadenie tak, aby sa čo najviac priblížil k hodnotám ocenenia DDZ. Štandardom je pri plánovaní dodržať hodnotu výroby s čo najlepším dosiahnutím tvaru výkonového nasadenia výrobných zariadení. Príklad takéhoto nasadenia DDZ je na obrázku 2.21. Zároveň je vidieť, v ktorých hodinách sú požiadavky na minimálne nasadenie a výkonové špičky počas celého dňa. | Ocenenie DDZ - Tento vstupný parameter vyjadruje výrobu v MWh a hodnotu veľkosti nasadenia v MW pre každú hodinu dňa. Takýmto spôsobom sú určené váhové hodnoty jednotlivých hodín, ktoré vyjadrujú veľkosť nasadenia energetických zariadení do prevádzky. Optimalizačný model v závislosti od ostatných vstupných podmienok navrhne nasadenie tak, aby sa čo najviac priblížil k hodnotám ocenenia DDZ. Štandardom je pri plánovaní dodržať hodnotu výroby s čo najlepším dosiahnutím tvaru výkonového nasadenia výrobných zariadení. Príklad takéhoto nasadenia DDZ je na obrázku 2.21. Zároveň je vidieť, v ktorých hodinách sú požiadavky na minimálne nasadenie a výkonové špičky počas celého dňa. | ||
| − | [[Súbor: | + | [[Súbor:Narh_2.21.png|framed|center|Obr. 2.21 Diagram denného zaťaženia]] |
Prítok vody v jednotlivých medzipovodiach - Pre správnosť výpočtu sa musí objem vody, ktorý sa vlieva do vodnej nádrže rovnať objemu vody, ktorý sa z vodnej nádrže vylieva. Jediná možná nerovnosť môže nastať v prípade, keď sa nádrž plní alebo prázdni. Hydrologický model je nosičom všetkých informácii a väzieb medzi údajmi. Optimalizačný model tieto údaje spracováva tak, aby sa dosiahlo najlepšie možné riešenie úlohy s cieľom eliminovať stratu informácii o prietokoch. Úlohu optimalizuje, pokiaľ nenájde riešenie na prevedenie celého energeticky využiteľného prietoku bez zostatku. Ak sa mu tento prietok nepodarí previesť celý, zvyšok objemu vody ponechá v nádrži. V opačnom prípade, keď použije väčšie množstvo vody spotrebovaný objem sa prejaví na koncovej hladine v nádrži. | Prítok vody v jednotlivých medzipovodiach - Pre správnosť výpočtu sa musí objem vody, ktorý sa vlieva do vodnej nádrže rovnať objemu vody, ktorý sa z vodnej nádrže vylieva. Jediná možná nerovnosť môže nastať v prípade, keď sa nádrž plní alebo prázdni. Hydrologický model je nosičom všetkých informácii a väzieb medzi údajmi. Optimalizačný model tieto údaje spracováva tak, aby sa dosiahlo najlepšie možné riešenie úlohy s cieľom eliminovať stratu informácii o prietokoch. Úlohu optimalizuje, pokiaľ nenájde riešenie na prevedenie celého energeticky využiteľného prietoku bez zostatku. Ak sa mu tento prietok nepodarí previesť celý, zvyšok objemu vody ponechá v nádrži. V opačnom prípade, keď použije väčšie množstvo vody spotrebovaný objem sa prejaví na koncovej hladine v nádrži. | ||
| Riadok 674: | Riadok 674: | ||
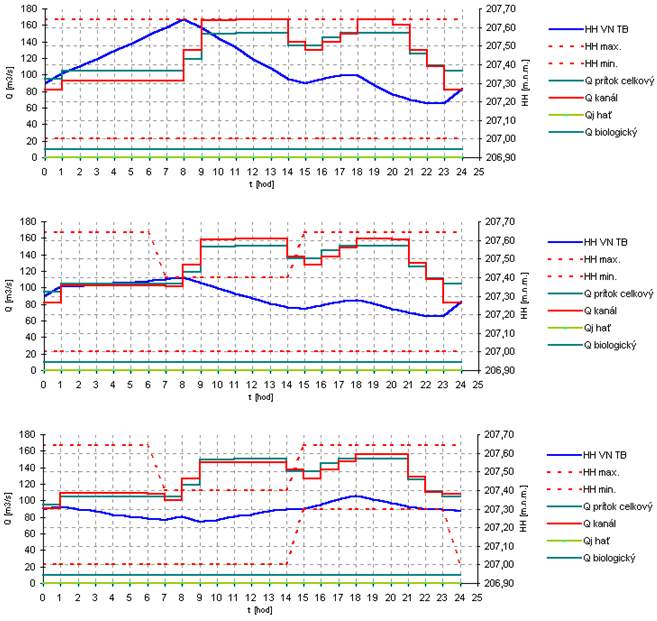
Počiatočné a koncové hladiny na jednotlivých vodných nádržiach - Prostredníctvom riadeného výpočtu sa z počiatočnej hladiny musíme priblížiť k plánovanej koncovej hladine vodnej nádrže daného dňa, prípadne ju dosiahnuť s čo najlepšie využitím prietoku hlavne cez energetickú časť. Koncová hladina sa v určitých prípadoch nedá dosiahnuť v presnej hodnote, ale podstata je priblížiť sa k nej čo najbližšie (Obr. 2.21). Situácia, kedy parameter koncovej hladiny nie je možné dodržať, je v čase veľmi nízkych denných prietokov cez SVK. Parametre minimálnych prevádzkových prietokov cez turbogenerátory sú v rozsahu desiatok m3.s-1, nie je teda možnosť jemného dolaďovania. Vzhľadom k tomu vyhodnotí model hladinu vyššiu alebo nižšiu, ako bola plánovaná. Na poslednom grafe obrázka 2.22 by sme mohli začať pochybovať o správnosti priebehu HH, je potrebné uvedomiť si, že optimalizačný model sa nielenže musí vyhnúť obmedzujúcim hladinám, ale čo je dôležité previesť potrebný objem vody na nasledujúci SVK a dodržať tak plánovanú koncovú hladinu. Pokiaľ počiatočná hladina nie je rovná koncovej plánovanej hladine, potom táto operácia znamená pre optimalizačný a hydrologický model zmenu v prietokovej bilancii jednotlivými SVK. | Počiatočné a koncové hladiny na jednotlivých vodných nádržiach - Prostredníctvom riadeného výpočtu sa z počiatočnej hladiny musíme priblížiť k plánovanej koncovej hladine vodnej nádrže daného dňa, prípadne ju dosiahnuť s čo najlepšie využitím prietoku hlavne cez energetickú časť. Koncová hladina sa v určitých prípadoch nedá dosiahnuť v presnej hodnote, ale podstata je priblížiť sa k nej čo najbližšie (Obr. 2.21). Situácia, kedy parameter koncovej hladiny nie je možné dodržať, je v čase veľmi nízkych denných prietokov cez SVK. Parametre minimálnych prevádzkových prietokov cez turbogenerátory sú v rozsahu desiatok m3.s-1, nie je teda možnosť jemného dolaďovania. Vzhľadom k tomu vyhodnotí model hladinu vyššiu alebo nižšiu, ako bola plánovaná. Na poslednom grafe obrázka 2.22 by sme mohli začať pochybovať o správnosti priebehu HH, je potrebné uvedomiť si, že optimalizačný model sa nielenže musí vyhnúť obmedzujúcim hladinám, ale čo je dôležité previesť potrebný objem vody na nasledujúci SVK a dodržať tak plánovanú koncovú hladinu. Pokiaľ počiatočná hladina nie je rovná koncovej plánovanej hladine, potom táto operácia znamená pre optimalizačný a hydrologický model zmenu v prietokovej bilancii jednotlivými SVK. | ||
| − | [[Súbor: | + | [[Súbor:Narh_2.22.png|framed|center|Obr. 2.22 Úprava obmedzujúcich HHTB pred a počas hladinového režimu]] |
Maximálne a minimálne prevádzkové hladiny nádrží a derivačných kanálov - Optimalizácia pri svojom výpočte musí riešiť prekročenie obmedzujúcich prevádzkových hladín a v prípade, že sú mimo povolený rozsah, musí riadiť postup riešenia úlohy spôsobom, ktorý tento neželaný stav odvráti. Príklad je uvedený na obrázku 2.22, kde sú zobrazené tri situácie s rovnakými vstupmi okrem obmedzujúcich HH. Aj v takomto prípade je snaha optimalizačného modelu tvarovať nasadenie podľa ocenenia DDZ. V prípade kanálov je táto úloha riešená z časti optimalizáciou prostredníctvom máp limitných prietokov a z časti hydrologickým modelom. Hydrologický model v kanálovej časti obsahuje pre jednotlivé derivačné kanále objemové krivky, ktoré majú rozsah od HHmin. po HHmax. Hydrologická časť umožňuje meniť tieto obmedzujúce hladiny v nádržiach (pohyb HHmin. aj pohyb HHmax.), ale v kanáloch je umožnené meniť iba HLNábehovú a DHmax. pod objektom VE. | Maximálne a minimálne prevádzkové hladiny nádrží a derivačných kanálov - Optimalizácia pri svojom výpočte musí riešiť prekročenie obmedzujúcich prevádzkových hladín a v prípade, že sú mimo povolený rozsah, musí riadiť postup riešenia úlohy spôsobom, ktorý tento neželaný stav odvráti. Príklad je uvedený na obrázku 2.22, kde sú zobrazené tri situácie s rovnakými vstupmi okrem obmedzujúcich HH. Aj v takomto prípade je snaha optimalizačného modelu tvarovať nasadenie podľa ocenenia DDZ. V prípade kanálov je táto úloha riešená z časti optimalizáciou prostredníctvom máp limitných prietokov a z časti hydrologickým modelom. Hydrologický model v kanálovej časti obsahuje pre jednotlivé derivačné kanále objemové krivky, ktoré majú rozsah od HHmin. po HHmax. Hydrologická časť umožňuje meniť tieto obmedzujúce hladiny v nádržiach (pohyb HHmin. aj pohyb HHmax.), ale v kanáloch je umožnené meniť iba HLNábehovú a DHmax. pod objektom VE. | ||
| − | [[Súbor: | + | [[Súbor:Narh_2.23.png|framed|center|Obr. 2.23 Úprava nábehovej hladiny na kanáli HR-MI]] |
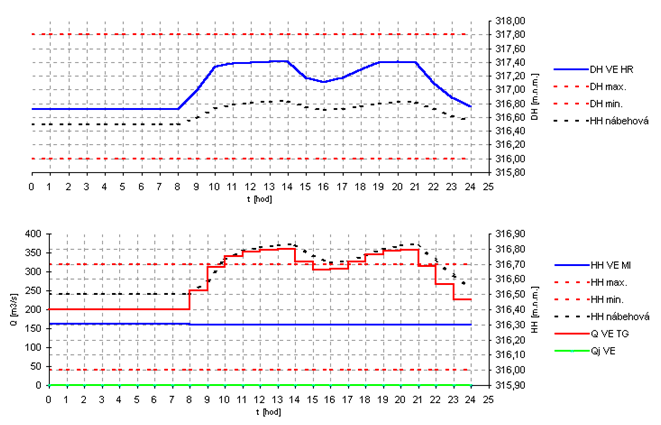
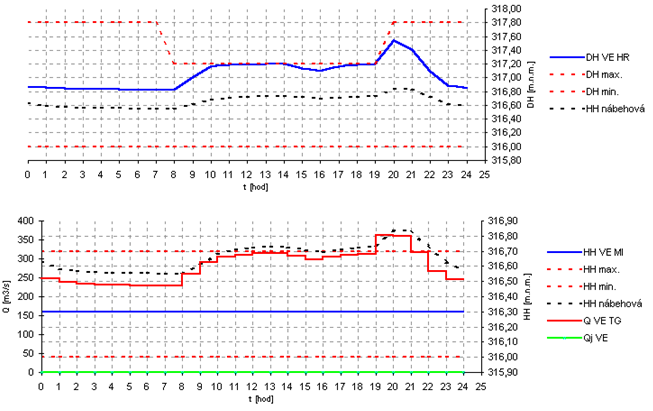
Optimalizačný model musí uvažovať s hladinovým režimom, či už v nádrži alebo v kanáli. V určitých prípadoch môže nastať obmedzenie do takej miery, že prietoky dosiahnu minimálnu hodnotu pre prevádzku TG na objektoch VE, prípadne úplné odstavenie VE z prevádzky. Na obrázku 2.23 je kanál medzi VE HR a VE MI. Pri väčších prietokoch model upravuje nábehovú hladinu tým, že začne plniť kanál potrebným množstvom vody. Pri hladinovom režime od 8:00 do 19:00, ktorý zobrazuje obrázok 2.24, je vidieť reakciu DHmax. na VE HR a zvýšenie prietoku modelom v ostatných hodinách dňa cez SVK HR-MI-PB. Rovnako ako v príklade TB (Obr. 2.22) všetky vstupy do modelu sú rovnaké, okrem obmedzenia DHmax. | Optimalizačný model musí uvažovať s hladinovým režimom, či už v nádrži alebo v kanáli. V určitých prípadoch môže nastať obmedzenie do takej miery, že prietoky dosiahnu minimálnu hodnotu pre prevádzku TG na objektoch VE, prípadne úplné odstavenie VE z prevádzky. Na obrázku 2.23 je kanál medzi VE HR a VE MI. Pri väčších prietokoch model upravuje nábehovú hladinu tým, že začne plniť kanál potrebným množstvom vody. Pri hladinovom režime od 8:00 do 19:00, ktorý zobrazuje obrázok 2.24, je vidieť reakciu DHmax. na VE HR a zvýšenie prietoku modelom v ostatných hodinách dňa cez SVK HR-MI-PB. Rovnako ako v príklade TB (Obr. 2.22) všetky vstupy do modelu sú rovnaké, okrem obmedzenia DHmax. | ||
| − | [[Súbor: | + | [[Súbor:Narh_2.24.png|framed|center|Obr. 2.24 Úprava hladinového režimu na kanáli HR-MI]] |
Dostupnosť energetických zariadení (TG) - V čase nedostupnosti energetického zariadenia na objekte VE sa môže plánovanie zamerať aj smerom celkového využitia objemu vody tak, aby nebolo zbytočne prevedené neenergeticky cez kanál, prípadne haťový objekt. Prevedenie vody nastane v čase dostupnosti TG, čím sa hospodárne využije hydroenergetický potenciál. Môžu nastať aj situácie, v ktorých by bez takéhoto prístupu nastalo plánované neenergetické prevedenie vody. Hydrologický model obsahuje informácie o možnostiach a na základe informácií, ktoré má k dispozícií, rieši optimalizačný model úlohu plánovania. Prioritne sa plánovanie zameriava na celkové prevedenie prietoku cez derivačný kanál, iba v špecifických prípadoch cez haťový objekt do starého koryta. No obrázku 2.25 je príklad nedostupnosti dvoch TG na VE KR v čase 11:00 až 14:00. Optimalizačný model preto časť výroby presunul do ranných hodín od 2:00 do 4:00. | Dostupnosť energetických zariadení (TG) - V čase nedostupnosti energetického zariadenia na objekte VE sa môže plánovanie zamerať aj smerom celkového využitia objemu vody tak, aby nebolo zbytočne prevedené neenergeticky cez kanál, prípadne haťový objekt. Prevedenie vody nastane v čase dostupnosti TG, čím sa hospodárne využije hydroenergetický potenciál. Môžu nastať aj situácie, v ktorých by bez takéhoto prístupu nastalo plánované neenergetické prevedenie vody. Hydrologický model obsahuje informácie o možnostiach a na základe informácií, ktoré má k dispozícií, rieši optimalizačný model úlohu plánovania. Prioritne sa plánovanie zameriava na celkové prevedenie prietoku cez derivačný kanál, iba v špecifických prípadoch cez haťový objekt do starého koryta. No obrázku 2.25 je príklad nedostupnosti dvoch TG na VE KR v čase 11:00 až 14:00. Optimalizačný model preto časť výroby presunul do ranných hodín od 2:00 do 4:00. | ||
| − | [[Súbor: | + | [[Súbor:Narh_2.25.png|framed|center|Obr. 2.25 Obmedzenie prevádzky TG na VE KR]] |
Obmedzenia hladinovej a prietokovej prevádzky - Ako už bolo spomenuté v bode maximálnych a minimálnych prevádzkových hladín, v modeli je možnosť plánovania hladinových obmedzení. Hydrologický model obsahuje aj vstup pre čisto prietokové obmedzenie cez SVK. Optimalizačný model v prípade kombinácie jednotlivých hladinových a prietokových obmedzení, analyzuje najvýznamnejšie obmedzenie (to, ktoré viac ovplyvní prietok cez SVK) a to aplikuje vo výpočte úlohy. Predchádza sa tak aj spomínanej strate informácií o prietokoch. Ak by optimalizačný model nepočítal so spomínaným prípadom, potom výsledky, ktoré postúpi hydraulicko-transformačnému modelu sa nenávratne stratia. Ovplyvnil by sa výsledok skutočného nasadenia TG na VE, čo by spôsobilo v operatívnom riadení rozladenie prevádzky zdrojov a nutnosť korekcie výkonov zdrojmi navzájom. | Obmedzenia hladinovej a prietokovej prevádzky - Ako už bolo spomenuté v bode maximálnych a minimálnych prevádzkových hladín, v modeli je možnosť plánovania hladinových obmedzení. Hydrologický model obsahuje aj vstup pre čisto prietokové obmedzenie cez SVK. Optimalizačný model v prípade kombinácie jednotlivých hladinových a prietokových obmedzení, analyzuje najvýznamnejšie obmedzenie (to, ktoré viac ovplyvní prietok cez SVK) a to aplikuje vo výpočte úlohy. Predchádza sa tak aj spomínanej strate informácií o prietokoch. Ak by optimalizačný model nepočítal so spomínaným prípadom, potom výsledky, ktoré postúpi hydraulicko-transformačnému modelu sa nenávratne stratia. Ovplyvnil by sa výsledok skutočného nasadenia TG na VE, čo by spôsobilo v operatívnom riadení rozladenie prevádzky zdrojov a nutnosť korekcie výkonov zdrojmi navzájom. | ||
| Riadok 704: | Riadok 704: | ||
**Minimálne obmedzenia každej VE je súčasťou máp limitných prietokov a slúži na stanovenie minimálneho prietoku cez objekty VE daného SVK. Je to z dôvodu, aby nebol podkročený minimálny prietok jedeného z objektov VE v priebehu hydromodelovania, čím by hydraulicko-transformačný model vylúčil tento objekt z prevádzky. Dôležité je to pri plánovaní vody a výroby z nej. | **Minimálne obmedzenia každej VE je súčasťou máp limitných prietokov a slúži na stanovenie minimálneho prietoku cez objekty VE daného SVK. Je to z dôvodu, aby nebol podkročený minimálny prietok jedeného z objektov VE v priebehu hydromodelovania, čím by hydraulicko-transformačný model vylúčil tento objekt z prevádzky. Dôležité je to pri plánovaní vody a výroby z nej. | ||
| − | Pre optimalizáciu sú mapy zdrojom informácií, pomocou ktorých v predstihu dokáže predikovať situáciu a správne plánovať vodu tak, aby nedochádzalo k strate informácií o vode a o nasadenom výkone objektov VE, ako aj o celkovej práci vážskej kaskády. Významne sa prostredníctvom máp ovplyvní čas výpočtu riešenej úlohy a v prípadoch veľkých vôd aj jej konečnosť a riešiteľnosť. | + | Pre optimalizáciu sú mapy zdrojom informácií, pomocou ktorých v predstihu dokáže predikovať situáciu a správne plánovať vodu tak, aby nedochádzalo k strate informácií o vode a o nasadenom výkone objektov VE, ako aj o celkovej práci vážskej kaskády. Významne sa prostredníctvom máp ovplyvní čas výpočtu riešenej úlohy a v prípadoch veľkých vôd aj jej konečnosť a riešiteľnosť. |
===Výstupné parametre optimalizačného modelu=== | ===Výstupné parametre optimalizačného modelu=== | ||
Verzia zo dňa a času 14:38, 7. december 2010
| 1. | Základné teoretické rovnice prúdenia v otvorených korytách |
| 2. | Opis modelovaného systému a jednotlivých častí hydromodelu |
| 3. | Hydromodelovanie vážskej kaskády
|
Obsah
- 1 Opis modelovaného systému a jednotlivých častí hydromodelu
- 1.1 Úloha hydromodelu a opis jeho jednotlivých častí
- 1.2 Prehľad stupňov vážskej kaskády
- 1.3 Rozdelenie VD na základné skupiny
- 1.4 Hydrologický model
- 1.5 Hydraulický model
- 1.6 Vyhodnotenie parametrov pre kanál
- 1.7 Podporné metódy a funkcie pre hydromodel
- 1.8 Transformačný model
- 1.9 Optimalizačný model
Opis modelovaného systému a jednotlivých častí hydromodelu
Úloha hydromodelu a opis jeho jednotlivých častí
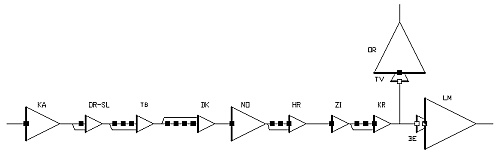
Tento programový nástroj je matematicko-logickým opisom reálneho objektu, ktorý sa skladá zo skupín, ktorým patria objekty a nakoniec prvky na výrobu elektrickej energie.
- Skupiny = SVK - Stupeň vážskej kaskády
- Objekty = VE – Vodná elektráreň
- Prvky = TG – Turbogenerátor
Hydromodelovanie bude obsahovať zjednodušenia, ktoré budú platné pre všetky SVK, a to:
- Horná hladina vodnej nádrže bude pri ľubovoľnom prietoku cez príhaťovú VE rovnaká ako hladina v nádrži a nebude vyhodnocovaná hydraulická strata pred týmto objektom. Bude to z dôvodu, že nedisponujeme platnými hodnotami hydraulickej straty pri rôznych prietokoch a rôznych prevádzkových hladinách vodnej nádrže;
- Takisto nebudú vyhodnocované straty v tlakových privádzačoch na VE, nakoľko neboli dostupné konštrukčné parametre týchto objektov. Chyba spôsobená zanedbaním hydraulickej straty bude malá a kompenzovaná hydraulickými stratami vyhodnotenými v kanáloch;
- Nebudú uvažované zanesenia hrubých hrablíc na haťových objektoch pri vstupe do prívodných kanálov pre VE a takisto jemných hrablíc priamo na prívodnom objekte VE (vstup do špirály).
Hydromodel sa bude skladať z častí - hydrologický, hydraulický, transformačný a optimalizačný model.
- Hydrologický model predstavuje systém medzipovodí, do ktorých vstupujú parametre prítoku z vyššie postavených nádrží, bočné prítoky a odtoky cez objekty z medzipovodí s energetickým alebo neenergetickým využitím. Maximálne a minimálne prevádzkové hladiny s možnosťou obmedzenia hladín v špecifických prevádzkových prípadoch. Takisto aj obmedzenia v dostupnosti energetických zariadení (GO, BO, REK, EZ, IV). Súčasťou hydrologického modelu budú mapy limitných prietokov pre kaskády a elektrárne prislúchajúcich vodných nádrží, ktoré zodpovedajú hladinám na vodných nádržiach a kanáloch, raster s krokom 0,05 m pre celý rozsah prevádzkových hladín. Tieto prietokové mapy budú vyhodnotené od povodňových vôd až po bežné prietokové režimy (hltnosť vodnej elektrárne, derivačného kanála), ktoré dokáže daný stupeň energeticky spracovať prípadne neenergeticky previesť cez derivačný kanál. Súčasťou budú takisto dotokové časy vody pre kanál a jalové vody cez hať pre staré korytá medzi jednotlivými stupňami. Výstupom tohto modelu budú údaje o prietokoch cez SVK na jednotlivých nádržiach v časovom rozsahu 23 až 25 hodín v hodinovom rastri.
- Hydraulický model pre derivačný kanál na základe výsledkov hydrologického a optimalizačného modelu navrhne hydraulické straty (nastavenie) hladín kanálov jednotlivých stupňov vážskej kaskády. Táto hydraulická závislosť bude vyhodnotená aj na kanáloch pod poslednou VE danej kaskády, kde odpadový kanál zaúsťuje do nasledujúcej vodnej nádrže prípadne koryta rieky. Horná hladina vodnej nádrže bude hydrostatická, rovná hladine vodnej nádrže bez ovplyvnenia drsností nádrže pri rôznych prietokoch, ale hladina na konci odpadového kanála (poslednej VE SVK) ústiaceho do nádrže, bude vyhodnotená cez minimálny potenciál z DH odpadového kanála pod VE. Výstupom tohto modelu budú teda spádové pomery na jednotlivých elektrárňach.
- Transformačný model na základe prietoku, spádu, účinnosti a dostupnosti technologického zariadenia bude dávať výsledok v podobe výkonového zaťaženia pre danú elektráreň a hodinu s presným počtom nasadených turbogenerátorov.
- Optimalizačný model má za úlohu na základe vstupných podmienok a obmedzení z hydrologického modelu navrhnúť prietokové pomery, rešpektujúc okrajové podmienky prevádzkových hladín a prietokov. Pri optimalizácii sa použije aj časť hydraulického modelu, a to hydraulický model nádrže, na vytvarovanie priebehu hladiny v nádrži. Nasadenie jednotlivých turbogenerátorov do prevádzky bude plánované prostredníctvom prietokového množstva vody cez objekt VE s obmedzeniami prietoku v závislosti od pozície hladiny v nádrži a rezervy prietoku pre regulačnú službu v časovom rozsahu 23 až 25 hodín v hodinovom rastri.
Jednotlivé modely budú pracovať ako celky pod názvom hydrologicko-optimalizačný a hydraulicko-transformačný.
Prehľad stupňov vážskej kaskády
Hydromodel bude pozostávať z nasledujúcich stupňov vážskej kaskády a k nim prislúchajúcimi elektrárňami spolu s počtom turbogenerátorov podľa [5] až [14]:
- VN Orava – VE Orava (OR) – 2xTG;
- VN Tvrdošín – VE Tvrdošín (TV) – 3xTG;
- VN Liptovská Mara – VE Liptovská Mara (LM) – 4xTG;
- VN Bešeňová – VE Bešeňová (BE) – 2xTG;
- VN Krpeľany – VE Krpeľany (KR) – 3xTG, VE Sučany (SU) – 3xTG, VE Lipovec (LI) – 3xTG;
- VN Žilina – VE Žilina (ZI) – 2xTG;
- VN Hričov – VE Hričov (HR) – 3xTG, VE Mikšová (MI) – 3xTG, VE Považská Bystrica (PB) – 3xTG;
- VN Nosice – VE Nosice (NO) – 3xTG;
- VN Dolné Kočkovce – VE Ladce (LA) – 2xTG, VE Ilava (IL) – 2xTG, VE Dubnica (DU) – 2xTG, VE Trenčín (TN) – 2xTG;
- VN Trenčianske Biskupice – VE Kostolná (KO) – 2xTG, VE Nové Mesto (NM) – 2xTG, VE Horná Streda (HS) – 2xTG;
- VN Sĺňava – VE Madunice (MA) – 3xTG;
- VN Kráľová – VE Kráľová (KA) – 2xTG.
Rozdelenie VD na základné skupiny
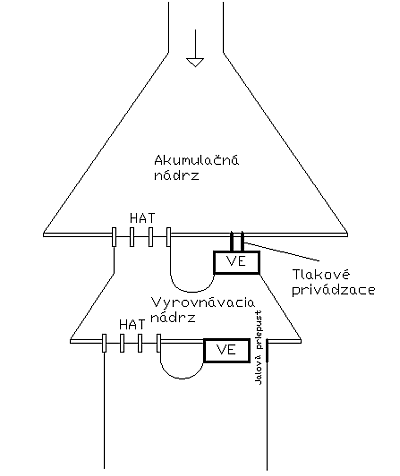
Jednotlivé VD z hľadiska hospodárenia s vodou a nasadzovania VE do prevádzky môžeme rozdeliť na [2]:
- Akumulačné VD - sú prevádzkované prostredníctvom hladiny vo vyrovnávacej nádrži, z ktorej je odtok vody riadený prietokovou reguláciou.
- Regulačné VD - sú prevádzkované v medziach prevádzkových hladín danej nádrže a odtoky sú riadené výkonovou reguláciou (v tomto prípade je dôležitý výkon aj napriek tomu, že výkon sa riadi cez prietok).
Medzi akumulačné VD patrí VN Orava a Liptovská Mara. Perióda prázdnenia a plnenia akumulačnej vodnej nádrže je jeden rok a vyrovnávacej vodnej nádrže, ktorá sa nachádza pod nimi, je táto perióda jeden deň.
Medzi regulačné VD patrí VN Tvrdošín, Bešeňová, Krpeľany, Žilina, Hričov, Dolné Kočkovce, Trenčianske Biskupice, Madunice, tu je perióda jeden deň a VN Nosice, Kráľová, tu je perióda prázdnenia a plnenia jeden týždeň.
Čas periód plnenia a prázdnenia je závislý od veľkosti vodnej nádrže a od významu pre sústavu celej vážskej kaskády. Nádrž z ročným vyrovnaním hladín sa nachádza nad všetkými VN vážskej kaskády a jej význam je v čase prebytku vody (z dažďov, topenia snehov) túto akumulovať a v čase nedostatku vody (letné mesiace, zimné mesiace) v jednotlivých medzipovodiach dotovať zvýšenými odtokmi. Nádrž z týždenným vyrovnaním (ako je VD NO) zabezpečuje vodu pre nižšie postavené SVK na pološpičkovú (priebežnú až špičkovú), alebo špičkovú (nasadenie je realizované v čase dňa) prevádzku a zároveň slúži na zachytenie vody zo špičkovej prevádzky vyššie postaveného stupňa. Zároveň zachytáva vodu z prívalových letných búrok a tým zmierňuje ekonomické straty na nevyužitý hydroenergetický potenciál v tejto časti Váhu. Prevádzka nádrží z denným vyrovnaním hladín je závislá od momentálnej situácie bočných prítokov do jednotlivých medzipovodí, kde sa tieto nádrže nachádzajú. V čase, kedy je možné túto vodu zachytiť, sa nasadzovanie orientuje do denných hodín. Inak sa na danom stupni realizuje pološpičková, v špecifických prípadoch priebežná prevádzka (povodne, prietokové alebo hladinové režimy).
Z pohľadu prevádzky môžeme VE rozdeliť na:
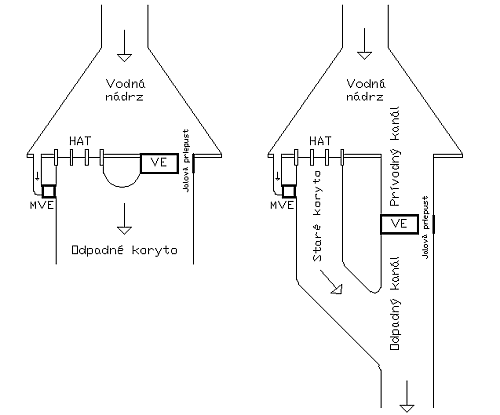
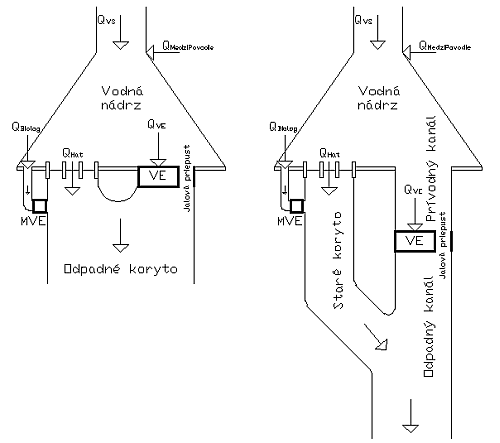
- Príhaťové elektrárne - nachádzajú sa v tesnej blízkosti vodnej nádrže a v rámci hydromodelovania horná hladina na týchto VE sa bude považovať za hydrostatickú. Pod objektom VE sa môže nachádzať odpadový kanál alebo staré koryto.
- Kanálové elektrárne - nachádzajú sa na prívodnom kanáli z vodnej nádrže alebo vyššie postavenej VE a vodu odvádzajú odpadovým kanálom k nasledujúcej VE, prípadne do nádrže alebo koryta rieky.
Hydrologický model
Tento model poskytuje údaje o prietokoch cez jednotlivé SVK. Poskytuje údaje o všetkých prietokoch do nádrží vstupujúcich a z nádrží vystupujúcich. Limitné hodnoty prietokov, ktoré je možné previesť derivačnými kanálmi a spracovať tak cez objekty VE, boli analyzované a vyhodnotené do máp limitných prietokov prostredníctvom vytvoreného hydraulicko-transformačného modelu. Úlohou týchto máp je popísať limitné prietoky pre optimalizačnú metódu ešte pred samotným odoslaním do hydraulicko-transformačného modelu, aby nenastal stav, ktorý by mal za následok vrátenie príliš veľkého množstva vody (prebytok alebo nedostatok) späť na prehodnotenie a úpravu obmedzujúcich prietokov do optimalizačného modelu. Ak by sme s limitnými prietokmi neuvažovali, pri samotnom spustení optimalizovania a riešenia konkrétnej úlohy by sme mohli naraziť na stav, ktorý by spôsobil enormné predĺženie času spracovania alebo veľmi skreslené výsledky. V úlohách pri riešení veľkých vôd by sme správny výsledok ani nevypočítali. Tým by sa stal celý nástroj nepoužiteľný!
Väzby v hydrologickom modeli vážskej kaskády môžeme rozdeliť do bodov:
- Prietoky vstupujúce a vystupujúce v danom profile (medzipovodí);
- Dotokové časy vody na úseku medzi jednotlivými stupňami v bežnej prevádzke VE;
- Dotokové časy jalovej vody cez hať a staré koryto do nasledujúceho profilu (medzipovodia).
Prietoky vstupujúce a vystupujúce v danom profile (medzipovodí)
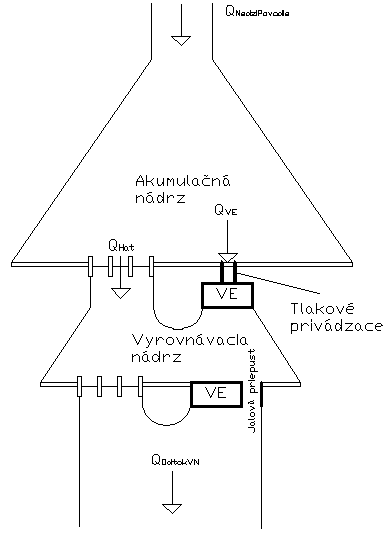
Riadenie prietoku cez VE na akumulačnom VD je závislé od odtoku z vyrovnávacej vodnej nádrže a tiež od objemu plnenia alebo prázdnenia tejto nádrže. Základnú rovnicu pre riadenie vody VD akumulačného typu môžeme vyjadriť ako:
|
[math]\overline{{{Q}_{VE}}}=\frac{\frac{\left( {{V}_{kon\operatorname{cov}\acute{y}}}-{{V}_{po\check{c}iato\check{c}n\acute{y}}} \right)}{3600}+\sum\limits_{krok=1}^{t}{{{Q}_{OdtokVN\left( krok \right)}}}-\sum\limits_{krok=1}^{t}{{{Q}_{MedziPovodie\left( krok \right)}}}-\sum\limits_{krok=1}^{t}{{{Q}_{Ha\check{t}\left( krok \right)}}}}{{{t}_{hodiny}}}[/math] |
(2.1) |
kde:
| t | časový interval výpočtu [hod]; |
| krok | krok výpočtu [hod]; |
| [math]\overline{{{Q}_{VE}}}[/math] | priemerný prietok vody cez VE z akumulačnej nádrže za interval t [m3.s-1]; |
| [math]V_{Počiatočný}[/math] | objem vyrovnávacej nádrže na začiatku intervalu t [[math]m^3[/math]]; |
| [math]V_{Koncový}[/math] | objem vyrovnávacej nádrže na konci intervalu t [[math]m^3[/math]]; |
| [math]ΣQ_{OdtokVN}[/math] | suma plánovaných odtokov z vyrovnávacej nádrže pre nadlepšovanie výroby za interval t [[math]m^3.s_{-1}[/math]]; |
| [math]ΣQ_{MedziPovodie}[/math] | suma predikcie bočného prítoku vody do profilu vyrovnávacej vodnej nádrže za interval t [[math]m^3.s_{-1}[/math]]; |
| [math]ΣQ_{Hať}[/math] | suma jalových odtokov z akumulačnej nádrže cez hať za interval t [[math]m^3.s_{-1}[/math]]; |
Základnú rovnicu riadenia vody pre typ regulačného VD môžeme vyjadriť ako:
|
[math]\overline{{{Q}_{VE}}}=\frac{\frac{\left( {{V}_{po\check{c}iato\check{c}n\acute{y}}}-{{V}_{kon\operatorname{cov}\acute{y}}} \right)}{3600}+\sum\limits_{krok=1}^{t}{{{Q}_{VS\left( krok \right)}}}-\sum\limits_{krok=1}^{t}{{{Q}_{MedziPovodie\left( krok \right)}}}-\sum\limits_{krok=1}^{t}{{{Q}_{Biolog\left( krok \right)}}}-\sum\limits_{krok=1}^{t}{{{Q}_{Ha\check{t}\left( krok \right)}}}}{{{t}_{hodiny}}}[/math] |
(2.2) |
kde:
| t | časový interval výpočtu [hod]; |
| krok | krok výpočtu [hod]; |
| [math]\overline{{{Q}_{VE}}}[/math] | priemerný prietok vody cez VE z akumulačnej nádrže za interval t [m3.s-1]; |
| [math]V_{Počiatočný}[/math] | objem nádrže na začiatku intervalu t [[math]m^3[/math]]; |
| [math]V_{Koncový}[/math] | objem nádrže na konci intervalu t [[math]m^3[/math]]; |
| [math]ΣQ_{VS}[/math] | suma plánovaných prítokov z vyššieho stupňa za interval t [m3.s-1]; |
| [math]ΣQ_{MedziPovodie}[/math] | suma predikcie bočného prítoku vody do profilu vyrovnávacej vodnej nádrže za interval t [[math]m^3.s_{-1}[/math]]; |
| [math]ΣQ_{Hať}[/math] | suma jalových odtokov z akumulačnej nádrže cez hať za interval t [[math]m^3.s_{-1}[/math]]; |
| [math]ΣQ_{Biolog}[/math] | suma biologických odtokov z nádrže na udržanie ekosystému v starom koryte [m3.s-1]; |
Dotokové časy vody na úseku medzi jednotlivými stupňami v bežnej prevádzke VE
Tento faktor v podstatnej miere ovplyvňuje časovú závislosť nasadenia VE medzi jednotlivými SVK, ktoré majú priamu, ale aj nepriamu hydraulickú väzbu. Pri nasadení VE to znamená významné ovplyvnenie chovania sa hladín vodnej nádrže a tým aj prevádzky VE v čase, keď voda je ešte len na ceste z vyššieho stupňa do daného profilu. Úseky derivačných kanálov nie je potrebné zaťažovať týmto časom (napriek tomu, že dotokové časy sú aj v kanáloch) z dôvodu rovnakého prietoku v čase cez prvú a poslednú VE daného SVK.
Medzi úseky, ktoré sú týmto významne ovplyvnené patria:
- VE Tvrdošín - VN Krpeľany;
- VE Bešeňová - VN Krpeľany;
- VE Lipovec - VN Žilina;
- VE Žilina - VN Hričov;
- VE Považská Bystrica - VN Nosice;
- VE Nosice - VN Dolné Kočkovce;
- VE Trenčín - VN Trenčianske Biskupice;
- VE Horná Streda - VN Sĺňava;
- VE Madunice - VN Kráľová.
Riešenie problému dotokových časov a transformáciu prietokovej vlny budeme realizovať pomocou vrstvových posunov v diskrétnom tvare. Tieto vrstvy budú vypočítané funkciou lineárnej interpolácie z bodov maximálneho a minimálneho prietoku a ich časovej závislosti dotoku z vyššie postavenej VE do nasledujúcej vodnej nádrže.
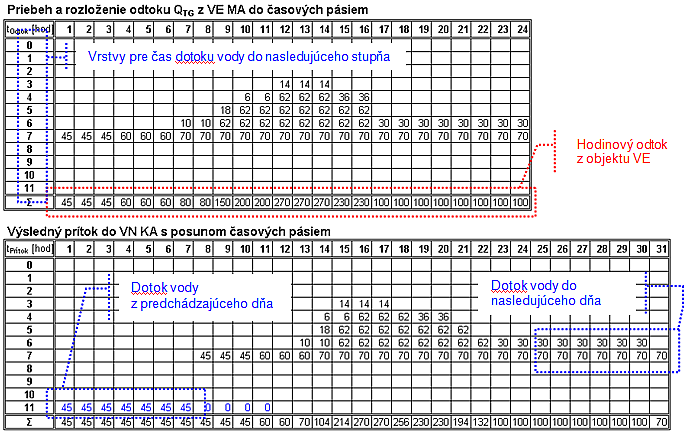
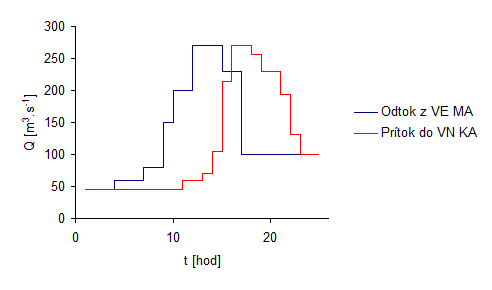
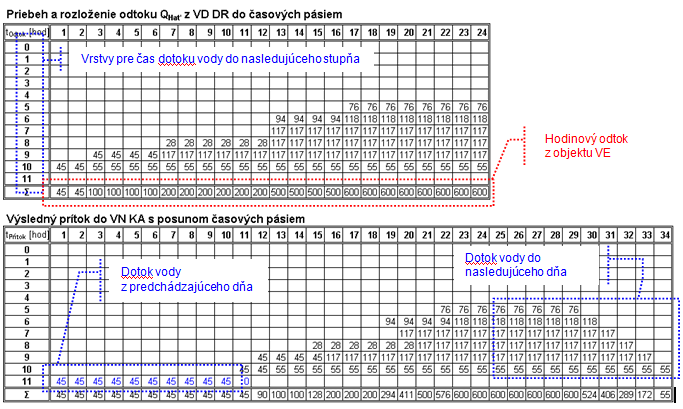
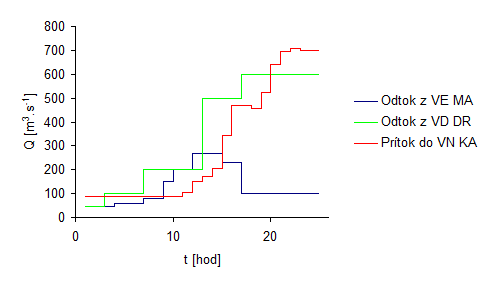
Pre priblíženie problému uvediem príklad, v ktorom bude stanovený odtok v každej hodine dňa z VE Madunice. Následne je každý odtok vyhodnotený funkciou [math]{{Q}_{t\left( krok \right)}}={{t}_{Dotok}}\left( {{Q}_{\Pr itok\left( krok \right)}} \right)[/math] , ktorá rozdelí odtok do časových vrstiev, v ktorých sa budú pohybovať k stanovenému cieľu. Výsledkom transformácie odtoku nám vznikne prítok s posunom jednotlivých časových vrstvách a teda aj prietokov pre jednotlivé hodiny dňa. Celý príklad ilustruje obrázok 2.7 a 2.8.
Veľmi dôležitý parameter bude pre nás suma odtoku a suma prítoku, ktoré sa musia rovnať za rovnaký časový interval, v opačnom prípade vnesieme chybu do celého výpočtu. Pomocou spomínaného riešenia sa dokážeme priblížiť k reálnemu priebehu prietokovej vlny, ktorej priebeh a časový posun je transformovaný do tvaru, ako je to uvedené na obrázku 2.8.
Vážska kaskáda má rôzne parametre dotokov vody medzi jednotlivými objektmi a stupňami, preto budú uvedené v tabuľke 2.1.
| Úsek medzi objektom a stupňom | Prietok [m3.s-1] | Čas dotoku t [hod] | Prietok [m3.s-1] | Čas dotoku t [hod] | |
| VE Orava - VE Tvrdošín | 800 | 0 | 15 | 0 | |
| VE Liptovská Mara - VE Bešeňová | 800 | 0 | 50 | 0 | |
| Lipovec - Žilina | 210 | 1,4 | 30 | 3,5 | |
| Žilina - Hričov | 720 | 0,3 | 60 | 0,75 | |
| Považská Bystrica - Nosice | 500 | 0,3 | 50 | 0,75 | |
| Nosice - Kočkovce | 390 | 0,3 | 40 | 0,75 | |
| Trenčín - Trenčianske Biskupice | 160 | 0,3 | 40 | 0,75 | |
| Horná Streda - Dráhovce | 180 | 0,6 | 40 | 1,5 | |
| Madunice - Kráľová | 300 | 2,8 | 40 | 7 |
Dotokové časy jalovej vody cez hať a staré koryto do nasledujúceho profilu (medzipovodia)
V čase veľkých vôd, kedy sú už kapacity energetického využitia vyčerpané, je potrebné ostatnú vodu previesť neenergeticky cez hať do koryta rieky. Má podobný časový charakter ako pri čisto energetickej prevádzke VE, riešený však bude úsek medzi jednotlivými SVK. Prevádzka VE je pri dosiahnutí určitých prietokov cez hať do koryta rieky po časovom intervale dotoku vody ďalej obmedzená. Je to spôsobené vzdutím dolnej hladiny pod objektom VE, kde obmedzujúce parametre spádových pomerov nie je možné dodržať. V takomto prípade bude hydraulický model znižovať prietokovú kapacitu turbogenerátorov na udržanie predpísaných spádových pomerov na jednotlivých objektoch VE.
Medzi úseky, ktoré sú týmto významne ovplyvnené patria:
- VD Tvrdošín - VN Krpeľany;
- VD Bešeňová - VN Krpeľany;
- VD Krpeľany - VN Žilina;
- VD Žilina - VN Hričov;
- VD Hričov - VN Nosice;
- VD Nosice - VN Dolné Kočkovce;
- VD Dolné Kočkovce - VN Trenčianske Biskupice;
- VD Trenčianske Biskupice - VN Sĺňava;
- VD Dráhovce - VN Kráľová.
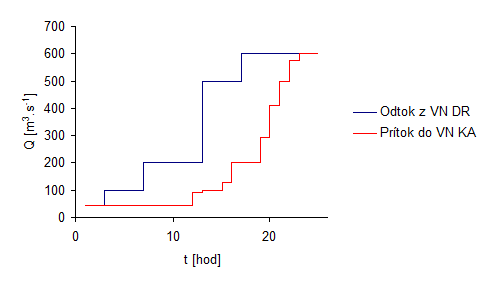
Riešenie problému dotokových časov a transformácia prietokovej vlny bude realizovaná rovnakou metódou ako v kapitole 2.4.2 pomocou vrstvových posunov v diskrétnom tvare. Nasledujúci príklad je počítaný medzi stupňami s jalovým prepadom cez haťový objekt VD DR (nadväzuje na predchádzajúci príklad). Výsledkom transformácie odtoku nám vznikne prítok s posunom jednotlivých časových vrstiev a teda aj prietokov pre jednotlivé hodiny dňa. Celý príklad ilustruje obrázok 2.10 a 2.11.
Rovnako ako v kapitole 2.4.2 suma odtoku a suma prítoku sa musí rovnať za rovnaký časový interval v opačnom prípade vnesieme chybu do celého výpočtu.
Vážska kaskáda má rôzne parametre dotokov vody medzi jednotlivými stupňami, preto budú uvedené v tabuľke 2.2.
| Úsek medzi objektom a stupňom | Prietok [m3.s-1] | Čas dotoku t [hod] | Prietok [m3.s-1] | Čas dotoku t [hod] | |
|---|---|---|---|---|---|
| VD Tvrdošín - VN Krpeľany | 800 | 4,5 | 5 | 11 | |
| VD Bešeňová - VN Krpeľany | 700 | 2,5 | 15 | 6,1 | |
| VD Krpeľany - VN Žilina | 700 | 3,4 | 20 | 8,3 | |
| VD Žilina - VN Hričov | 700 | 0,3 | 20 | 0,8 | |
| VD Hričov - VN Nosice | 700 | 3,5 | 20 | 8,6 | |
| VD Nosice - VN Dolné Kočkovce | 700 | 0,6 | 20 | 1,5 | |
| VD D. Kočkovce - VN T. Biskupice | 700 | 3,5 | 20 | 8,6 | |
| VD T. Biskupice - VN Sĺňava | 700 | 4,5 | 20 | 11 | |
| VD Dráhovce - VN Kráľová | 700 | 4 | 20 | 9,8 |
Ak by sme spojili oba príklady do jedného, vznikol by nám priebeh zobrazený na obrázku 2.12. Na celej vážskej kaskáde sú derivačné kanále a staré korytá Váhu zaústené veľmi blízko cieľa dotoku vody do vodnej nádrže, okrem zaústenia odpadového kanála pod objektom VE Lipovec a VE Madunice. Pre zjednodušenie tu bude prijatý rovnaký prístup, ako pri ostatných stupňoch vážskej kaskády.
Hydraulický model
Údaje vystupujúce z hydrologického modelu sú vstupnými pre hydraulický model. Úlohou hydraulického modelu je výpočet spádových pomerov a prietokových obmedzení, ktoré sú v súčinnosti s transformačným modelom ďalej vyhodnotené a doplnené do limitných prietokových máp. Pomocou limitných prietokových máp bude zabezpečená na úrovni optimalizovania korektnosť výpočtu maximálneho prietoku cez VE alebo derivačný kanál. Bude tým zabezpečená rýchla priechodnosť a konečnosť výpočtu. Hydraulický model bude mať za úlohu:
- Nastaviť pozíciu hladiny v nádrži;
- Určiť hydraulické väzby medzi jednotlivými VE;
- Vyhodnotiť hladinové režimy v derivačných kanáloch;
- Stanoviť maximá energeticky využiteľného prietoku pomocou predchádzajúcich bodov (mapa limitných prietokov).
Hydraulický model môžeme rozdeliť na nasledujúce úseky [2]:
- Nádrž;
- Úsek vodná nádrž – VE;
- Úsek VE – VE;
- Úsek VE – vodná nádrž;
- Úsek VE – koryto rieky.
Hydraulický model nádrže
Model pre nádrž má za úlohu stanoviť na základe počiatočnej a koncovej hladiny v nádrži voľný objem (pre plnenie) a zásobný objem (pre prázdnenie), ktorý treba započítať k prietokom z hydrologického modelu, čím je ďalej stanovený priemerný denný odtok z daného SVK. Priebežne bude z vypočítaných objemov v jednotlivých hodinách určovať pozíciu hladiny v nádrži. Teoreticky budeme uvažovať s hydrostatickou hladinou v nádrži pri rôznych prietokoch z dôvodu zjednodušenia. Deformáciu nádrže budeme riešiť nepriamo, ale táto metóda bude bližšie rozpracovaná pri úseku VE – vodná nádrž v kapitole 2.5.5 a VE – koryto rieky v kapitole 2.5.6.
Základné rovnice hydraulického modelu nádrže budú:
|
[math]{{V}_{Z\acute{a}sobn\acute{y}\ \left( krok \right)}}={{V}_{Z\acute{a}sobn\acute{y}\ \left( krok-1 \right)}}+{{Q}_{Celkov\acute{y}\ pr\acute{i}tok\left( krok \right)}}\cdot 3600-{{Q}_{Celkov\acute{y}\ odtok\left( krok \right)}}\cdot 3600[/math] |
(2.3) |
|
[math]H{{H}_{N\acute{a}dr\check{z}e}}=f\left( {{V}_{Z\acute{a}sobn\acute{y}\left( krok \right)}} \right)[/math] |
(2.4) |
kde:
| krok | krok výpočtu [hod]; |
| [math]V_{Zásobný}[/math] | objem nádrže na konci kroku výpočtu [m3]; |
| [math]V_{Zásobný(krok-1)}[/math] | objem nádrže na začiatku kroku výpočtu [[math]m^3[/math]]; |
| [math]Q_{Celkový prítok}[/math] | celkový prítok z vyššieho stupňa na konci kroku výpočtu [[math]m^3.s^{-1}[/math]]; |
| [math]Q_{Celkový odtok}[/math] | celkový odtok z nádrže na konci kroku výpočtu [[math]m^3.s^{-1}[/math]]; |
| [math]HH_{Nádrž}[/math] | pozícia hladiny vodnej nádrže na konci výpočtového kroku [m.n.m Bpv]. |
K dispozícii máme objemové krivky jednotlivých vodných nádrží, z ktorých budeme pomocou lineárnej interpolácie získavať hodnoty objemov a hladín aj na pozíciách, ktoré nie sú v krivkách uvedené. Jednoduchosť inverzie tejto funkcie nám zabezpečí absolútnu rovnosť hodnôt aj po niekoľkonásobnej transformácii objemu na hladinu a naopak pri následnom posune parametrov a cyklickom opakovaní (Obr. 2.13).
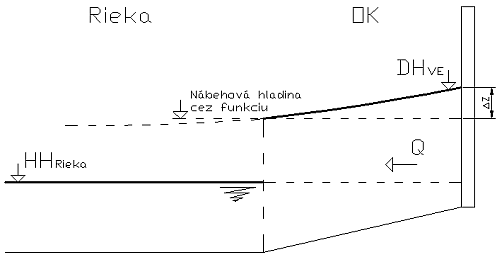
Hydraulický model kanálov
Úlohou hydraulického modelu kanálov je stanoviť hydraulické straty spôsobené drsnosťou kanálov a ďalšími faktormi (ako napr. prietok, nábehová hladina). Tieto straty sa premietnu do spádových pomerov pre jednotlivé objekty VE. Môžeme povedať, že derivačné kanále sa nachádzajú pri každej elektrárni s výnimkou VD KA. Preto tvorba tohto modelu bude z hľadiska výpočtu a vyhodnocovania jednotlivých vypočítaných parametrov s reálnymi parametrami, jednou s najnáročnejších úloh tejto práce.
Pri výpočtoch sa bude uvažovať v kanáloch s ustáleným prúdením vody napriek tomu, že pri zmenách prietoku ustálené prúdenie nastáva po dlhšom čase. Takýto prístup bude zvolený z dôvodu hľadania možného nasadenia vodných elektrární s časovým intervalom hodina, deň, týždeň, mesiac a rok. Nebudeme teda skúmať dynamiku vody v kanáli nad, ani pod objektom VE pri nábehoch, odstaveniach alebo zmenách v prietoku pri prevádzke.
Základnú rovnicu hydraulického modelu kanálov môžeme vyjadriť v tvare:
|
[math]\Delta {{z}_{(krok)}}=Q_{(krok)}^{2}\left[ \left( 1\pm \zeta \right)\cdot \frac{\alpha }{2g}\cdot \left( \frac{1}{S_{2(krok)}^{2}}-\frac{1}{S_{1(krok)}^{2}} \right)+\frac{Q_{(krok)}^{2}}{K_{p(krok)}^{2}}\Delta l \right][/math] |
(2.5) |
kde:
| krok | krok výpočtu v jednej hodine; |
| Δz | diferencia od nábehovej hladiny [m]; |
| Q | prietok prívodným alebo odpadným kanálom [[math]m^3.s^{-1}[/math]]; |
| ζ | súčiniteľ miestnej straty; |
| α | Coriolisovo číslo; |
| g | gravitačné zrýchlenie [[math]m.s^{2}[/math]]; |
| S1 | prietoková plocha (horný prietokový prierez) [[math]m^2[/math]]; |
| S2 | prietoková plocha (dolný prietokový prierez) [[math]m^2[/math]]; |
| Kp | Sp, Cp, Rp sú aritmetické priemery plôch [m2], rýchlostných súčiniteľov [[math]m^{0,5}.s^{-1}[/math]] a hydraulických polomerov [m] v hornom a dolnom priereze kde
[math]{{K}_{p}}={{C}_{p}}\cdot {{S}_{p}}\sqrt{{{R}_{p}}}[/math] |
| Δl | dĺžka kanála [m]. |
Súčasťou rovnice sú aj konštrukčné parametre kanála popísané v kapitole 1.2.1. Vstupnými parametrami pre výpočet bude prietok cez kanál a nábehová hladina v kanáli (ktorú bude možné pre celý rozsah hodín dňa meniť v rozsahu prevádzkových hladín).
Úsek vodná nádrž - VE
Úsek vodná nádrž – VE môžeme rozdeliť na úseky s prívodným kanálom a bez prívodného kanála na objekt VE. Nábehová hladina pre kanál alebo VE bude vyhodnocovaná z hladiny v nádrži pre daný výpočtový krok.
Medzi úseky s kanálom patria:
- VD Dolné Kočkovce – VE Ladce;
- VD Trenčianske Biskupice – VE Kostolná;
- VD Dráhovce (VN Sĺňava) – VE Madunice.
Medzi úseky bez prívodného kanála patria (nazývajú sa príhaťové VE):
- VN Tvrdošín – VE Tvrdošin;
- VN Bešeňová – VE Bešeňová;
- VN Krpeľany – VE Krpeľany;
- VN Žilina – VE Žilina;
- VN Hričov – VE Hričov;
- VN Nosice – VE Nosice;
- VN Kráľová – VE Kráľová.
Úsek VE - VE
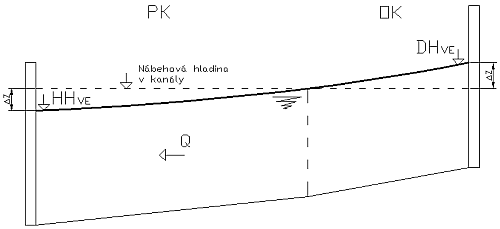
Na úseku VE – VE sa nachádza kanál, ktorý je rozdelený na dva (popísané technickou dokumentáciou):
- odpadný od VE;
- prívodný k VE.
Súčasťou týchto kanálov budú aj objemové krivky v rozsahu prevádzkových hladín. Významný rozmer nadobudnú vo chvíli, keď diferencia ∆z od nábehovej hladiny poklesne pod minimálnu prevádzkovú hladinu pre daný objekt VE, alebo prietok cez kanál dosiahne také hodnoty, ktoré znížia HH pod minimálnu prevádzkovú hodnotu, alebo sa zvýšia DH natoľko, že sa nedodrží minimálny spádový parameter pre TG objektu VE. V takom prípade hydromodel začne upravovať pozíciu nábehovej hladiny tak, aby prevádzkové obmedzenia zostali dodržané. Pri zmene pozície nábehovej hladiny v kanáli sa prepočíta plnenie alebo prázdnenie kanála, čo sa premietne do prietokových pomerov cez objekty VE daného SVK.
Medzi úseky tohto typu patria:
- VE Krpeľany – VE Sučany;
- VE Sučany - VE Lipovec;
- VE Hričov – VE Mikšová;
- VE Mikšová – VE Považská Bystrica;
- VE Ladce – VE Ilava;
- E Ilava – VE Dubnica;
- VE Dubnica – VE Trenčín;
- E Kostolná – VE Nové Mesto;
- VE Nové Mesto - VE Horná Streda.
Úsek VE – vodná nádrž
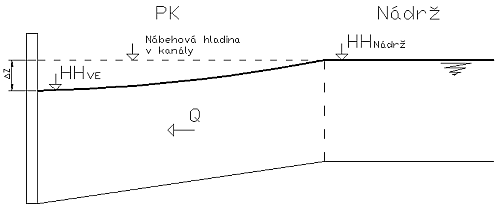
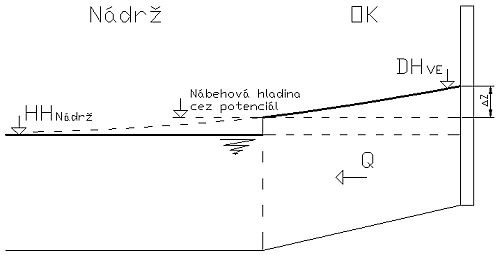
Úsek VE – vodná nádrž je kľúčový pri určovaní nepriameho naklonenia hladiny nádrže v bezprostrednej blízkosti odpadového kanála poslednej VE kaskády. Aby sme mohli hydraulicky prepojiť tento úsek s nádržou bolo potrebné vyhodnotiť vzdutie na konci odpadového kanála. Najlepším riešením tohto problému bolo nájsť najmenší potenciál vzdutia DH pod objektom VE. Vstupný parameter nábehovej hladiny v kanáli je hladina vodnej nádrže. Hydraulický model hľadá riešenie pre daný prietok, pokiaľ klesajúca DH nenaberie stúpajúcu tendenciu. V tomto okamihu je vyhodnotený najmenší potenciál DH a nastáva hydraulické spojenie odpadového kanála VE s nádržou nasledujúceho SVK.
Medzi úseky tohto typu patria:
- VE Orava – VN Tvrdošín;
- VE Liptovská Mara - VN Bešeňová;
- VE Žilina – VN Hričov;
- VE Považská Bystrica – VN Nosice;
- VE Nosice – VN Dolné Kočkovce;
- VE Trenčín – VN Trenčianske Biskupice;
- VE Horná Streda – VN Sĺňava.
Úsek VE – koryto rieky
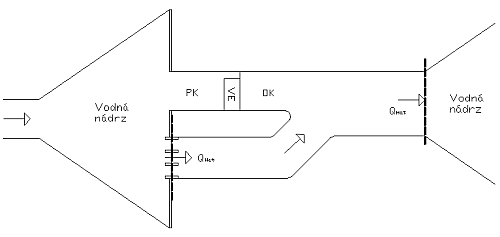
Úsek VE – koryto rieky môžeme rozdeliť na úseky s odpadovým kanálom a bez odpadového kanála od objektu VE. V prípade s odpadovým kanálom bude nábehová hladina vypočítaná funkciou, kde vstupný parameter na určenie nábehovej hladiny bude prietok VZOREC z VE. Úsek, kde sa kanál nenachádza bude DH vypočítaná priamo funkciou VZOREC . Z dôvodu, že na VD TV a BE sa prietok z VE a prietok cez hať stretávajú v bezprostrednej blízkosti pod VD (Obr. 2.2), DH je priamo počítaná cez funkciu.
Medzi úseky s kanálom patria:
- VE Tvrdošín – rieka Orava;
- VE Bešeňová – rieka Váh;
- VE Lipovec – rieka Váh;
- VE Madunice – rieka Váh.
Medzi úseky bez kanála patria:
- VE Kráľová – rieka Váh.
Vyhodnotenie parametrov pre kanál
Podľa konštrukčných parametrov derivačných kanálov vyhľadaných v technickej dokumentácii pre jednotlivé SVK bolo možné vytvoriť základy hydraulického modelu. Aby sme boli schopní použiť rovnicu pre výpočet hydraulických strát na jednotlivých úsekoch kanálov nevyhnutnou podmienkou je:
- Vytvoriť náhradu funkcie rýchlostného súčiniteľa (Chézyho súčiniteľ);
- Vyhodnotiť drsnosť kanálov z nameraných hodnôt HH a DH pri rôznych prietokových pomeroch.
Rýchlostný súčiniteľ
Rýchlostný súčiniteľ je hodnota vystupujúca v Chézyho vzťahu na výpočet strednej prierezovej rýchlosti v alebo Q. V našom prípade nastáva malý problém a to
- nemôžeme použiť Pavlovského empirický vzťah 1.15 z dôvodu platnosti hraníc 0,1m < R < 3,0m, kde v mnohých prípadoch hydraulický polomer kanálov dosahuje R > 5;
- máme k dispozícii diskrétne hodnoty v rozsahu 0,1m až 5,0m, ale my potrebujeme vyhodnotiť rýchlostný súčiniteľ aj nad uvedený parameter hydraulického polomeru.
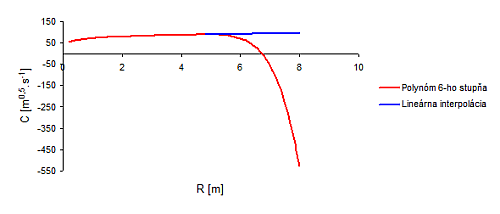
Tento problém vieme riešiť preložením bodov vhodnou polynómickou funkciou, ktorá s najmenšou odchýlkou bude vyhovovať našim požiadavkám. Pretože v tejto chvíli nevieme s určitosťou povedať, či pri zmene pozície nábehovej hladiny smerom k maximálnej prevádzkovej hladine zväčšíme hydraulický polomer kanála natoľko, že funkcia rýchlostného súčiniteľa sa začne vyhodnocovať nekorektne, musíme zabezpečiť jej plynulý prechod lineárnou interpolačnou funkciou cez posledné dve hodnoty. Teraz aj keď nevieme povedať aké skutočné hodnoty rýchlostného súčiniteľa sú nad R > 5 m, lineárnou funkciou zabezpečíme korektné správanie sa celého hydraulického modelu (Obr. 2.18). Pre potreby hydraulickej časti modelu budeme pracovať so stupňami drsností kanála n = {0,014; 0,017; 0,020; 0,025; 0,030; 0,035; 0,040}, pre ktoré vytvoríme funkcie polynómu.
Drsnosť kanálov
Meranie a vyhodnotenie drsností jednotlivých kanálov na vážskej kaskáde urobíme nepriamo pomocou hydraulického modelu. Musíme mať rôzne vzorky parametrov hladín a prietokov, ktoré ďalej vieme analyzovať v pripravenom hydraulickom modeli. Princíp vyhľadávania drsností kanálov je v nájdení najvhodnejšej kombinácie drsností prívodného a odpadového kanála. Pomocný nástroj, ktorý bude na tento účel naprogramovaný, v kanáloch hydromodelu nastaví nábehovú hladinu ako HHVE a cez prietok bude hľadať najbližšiu pozíciu DHVE. K dispozícii bude n vzoriek a pre každú urobí kompletné vyhodnotenie. Z najväčšieho počtu súhlasných kombinácii drsností všetkých vzoriek tieto použijeme do technických parametrov pre jednotlivé kanále. Matematicky to bude nasledovne:
VZOREC (2.6)
Odpadový a prívodný kanál počíta s rovnicou (2.6) samostatne aj napriek tomu, že vystupujú ako jeden celok. Všetky zložky budú konštantné pre parametre odpadového a prívodného kanála a staticky nastavené na prietok, ktorý cez ne preteká. Jediný meniaci sa parameter bude Chézyho súčiniteľ C [m0,5.s-1]. V rovnici (2.6) vystupuje už len jeho priemerná hodnota horného a dolného prietokového prierezu. Obidva kanále sa matematicky počítajú samostatne, ale HLNábehová, ktorej pozícia začala na HHVE sa posunie (Obr. 2.19) pri výpočte na začiatku prívodného kanála na úroveň prietoku cez kanál a od tejto HLNábehovej je ďalej počítaná DHVE.
Podporné metódy a funkcie pre hydromodel
Všetky doterajšie riešenia sa týkali úsekov derivačných kanálov na stupňoch vážskej kaskády bez ich priameho hydraulického prepojenia. V tejto chvíli vieme matematicky opísať hydraulický model od nádrže po posledný objekt VE každého stupňa. Podmienka dobrého návrhu hydromodelu je celkové hydraulické prepojenie stupňov vážskej kaskády. Každý stupeň má poslednú VE (v niektorých prípadoch je zároveň prvá), za ktorou je odpadový kanál ústiaci do vodnej nádrže alebo koryta rieky. Práve tieto úseky nás budú zaujímať a v návrhu modelu je potrebné rozpracovať nasledujúce:
- Navrhnúť hydraulické prepojenie odpadového kanála s vodnou nádržou nasledujúceho stupňa;
- Vytvoriť funkciu, ktorá bude opisovať pozíciu hladiny v rieke na konci odpadového kanála;
- Vytvoriť funkciu, ktorá bude opisovať pozíciu hladiny v rieke pri jalových vodách cez hať pod posledným objektom VE daného stupňa.
Hydraulické prepojenie odpadného kanála s vodnou nádržou nasledujúceho stupňa
Ako bolo spomenuté pri úseku VE – vodná nádrž jedná sa o miesto, ktoré nie je možné spojiť priamo z nádržou spôsobom nábehová hladina rovná sa hladina nádrže. Budeme hľadať riešenie, ako sa bude prakticky správať hladina nádrže na konci odpadového kanála pri rôznych prietokoch a hladinách v nádrži. Konštrukčné parametre kanála sú známe a vieme, že rôzne prietoky potrebujú rôzne minimálne prietokové plochy na to, aby sa cez kanál dostali do nádrže. Preto budeme hľadať najmenšiu prietokovú plochu prostredníctvom potenciálu najmenšieho vzdutia DH, ktorý začneme vyhodnocovať cez zmeny pozície nábehovej hladiny kanála. Samozrejme, ak hladina nádrže svojou pozíciou zabezpečí väčšiu prietokovú plochu ako je potrebné pre daný prietok, posun nábehovej hladiny sa zastaví na hladine nádrže. Princíp metódy bude nasledovný: pozícia nábehovej hladiny na začiatku bude v dostatočnej výške a to optimálne nad maximálnou DH pod VE. Metóda hľadania najmenšieho potenciálu DH pod VE je založená na znižovaní nábehovej hladiny, pokiaľ klesajúca DH nenaberie stúpajúcu tendenciu. V tomto bode sa hľadanie ukončí a máme tak vytvorené hydraulické spojenie jednotlivých stupňov vážskej kaskády.
Funkcia opisujúca pozíciu hladiny v rieke na konci odpadného kanála ústiaceho do rieky
Podobne, ako je to pri spojení odpadového kanála s vodnou nádržou, aj v tomto prípade musíme nepriamo vyhodnotiť hladiny rieky cez pripravený hydraulický model pre daný úsek Váhu. Opäť máme k dispozícii vzorku hladín v závislosti od prietoku cez VE. V tomto prípade nám pomocný výpočtový nástroj bude hľadať cez potenciál DH hladinu rieky pri danom prietoku. Vyhodnotené budú vzorky hladín cez stanovené drsnosti a konečný výber hladín rieky bude preložený vhodnou polynómickou funkciou.
Funkcia opisujúca pozíciu hladiny v rieke pri jalových vodách cez hať pod poslednou VE daného stupňa
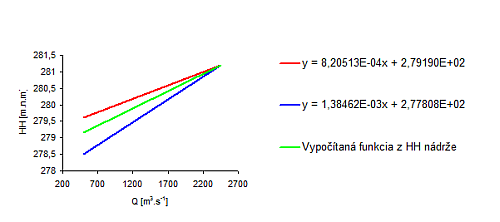
Jalové vody, ktoré sa opakujú raz za sto rokov budeme z časových dôvodov vyhodnocovať z meraní uvedených v technickej dokumentácii pre jednotlivé stupne vážskej kaskády. Vzhľadom k tomu, že vo väčšine prípadov sa udáva hladina storočných vôd pod VE, závislosť funkcie pod objektmi TV, ZI, HS, MA bude podľa známych bodov lineárna. Pod objektmi PB, TN bude závislosť tiež lineárna, ale zároveň vznikne nová dynamická funkcia spojená z dvoch lineárnych funkcií, jedna opisuje závislosť HHmin. a druhá HHmax. hladiny v nádrži pod danou VE od prietoku jalovej vody. Príklad spojenia týchto funkcii priblížime pre objekt VE PB a VN NO.
Funkcia pre max. hladinu nádrže: [math]y=0,000820513x+279,19[/math] Funkcia pre min. hladinu nádrže: [math]y=0,00138462x+277,808[/math]
kde [math]x={{Q}_{Celkov\acute{y}\ Jalov\acute{y}}}[/math]
Výpočet koeficienta [math]x^1[/math]:
[math]\begin{align} & Pomer\_koe{{f}^{1}}=\frac{0,000820513-0,00138462}{279,6-274,6}=-0,0001128214 \\ & {{k}^{1}}=0,000820513-Pomer\_koe{{f}^{1}}\left( 279,6-274,6 \right) \\ \end{align}[/math]
Výpočet koeficienta [math]x^0[/math]:
[math]\begin{align} & Pomer\_koe{{f}^{0}}=\frac{279,19-277,808}{279,6-274,6}=0,2764 \\ & {{k}^{0}}=279,19-Pomer\_koe{{f}^{0}}\left( 279,6-274,6 \right) \\ \end{align}[/math]
Funkcia popisujúca dynamické závislosti:
[math]\begin{align} & H{{H}_{Koniec\ OK}}={{k}^{1}}x+{{k}^{0}} \\ & H{{H}_{Koniec\ OK}}=\left[ 0,000820513+0,0001128214\cdot \left( 279,6-H{{H}_{N\acute{a}dr\check{z}\ Aktu\acute{a}\ln a}} \right) \right]\cdot {{Q}_{Celkov\acute{y}\ Jalov\acute{y}}}+ \\ & +279,19-0,2764\cdot \left( 279,6-H{{H}_{N\acute{a}dr\check{z}\ Aktu\acute{a}\ln a}} \right) \\ \end{align}[/math]
Závislosť hladín z jalovej vody cez hať na objektoch BE, KR, NO, KA bude opísaná polynómom n-tého stupňa.
Všetky uvedené funkcie opisujú závislosť HH (nádrže, rieky) na konci odpadového kanála poslednej VE od prietoku nad hltnosť VE alebo derivačného kanála. Pokiaľ nastane obmedzenie užívateľom cez stupeň do hltnosti objektov (ostatnú vodu prevedie model cez hať), hladina na konci odpadového kanála bude vyhodnotená metódou alebo funkciou, akoby sa jednalo o prietok cez objekty VE. Hydromodel v tomto prípade vyhodnotí aj časový posun, ktorý je potrebný pri prietoku korytom rieky z hate do cieľa pod objekt VE.
Transformačný model
Aby sme sa dopracovali k hľadanému výsledku, ktorým je elektrický výkon jednotlivých objektov VE, výsledky hydrologického a hydraulického modelu musíme transformovať. Na základe prietoku, spádu, účinnosti a dostupnosti technologického zariadenia transformačný model vypočíta elektrický výkon s presným počtom nasadených turbogenerátorov v jednotlivých hodinách dňa. Ďalšou úlohou modelu bude pri nedostupnosti jedného TG vyhodnotiť nasadenie ďalšieho dostupného TG do prevádzky. Základnú rovnicu transformačného modelu môžeme zapísať v tvare:
|
[math]{{P}_{(krok)}}=\frac{{{Q}_{(krok)}}\cdot g\cdot {{h}_{(krok)}}\cdot {{\eta }_{TG}}}{1000}[/math] |
(2.7) |
kde:
| krok | krok výpočtu v jednej hodine; |
| P | Elektrický výkon [MW]; |
| Q | Prietok vody cez TG [[math]m^3.s^{-1}[/math]]; |
| g | konštanta gravitačného zrýchlenia [[math]m.s^{-2}[/math]]; |
| h | spád (h = HH – DH) [m]; |
| ηTG | celková účinnosť (turbína + generátor) [%]. |
Inverzná transformácia elektrického výkonu
Inverzná transformácia bude slúžiť na vyjadrenie prietoku z regulačného výkonu SRV z prvej VE na derivačnom kanály. Aby sme dosiahli vyrovnanú bilanciu vody pri pôsobení regulačného signálu na objekty VE pri minimálnej a maximálnej požiadavke na SRV je potrebné, aby v rovnakom čase boli navrhnuté aj prietoky cez VE pri zmenách rovnako. Pomocou výkonu pre SRV bude vyhodnotený prietok na SRV prvej VE a pomocou spätnej transformácie môžeme počítať rezervu SRV pri daných spádových a prietokových pomeroch na ostatných VE príslušného derivačného kanála. Transformačný model bude aj na základe týchto výpočtov vyhodnocovať prevádzkové spustenie, prípadne odstavenie TG. Ak kapacita dosiahnuteľného výkonu bude vyčerpaná (jeden z TG bude z technických príčin mimo prevádzky), vodu ktorú hydrologický a hydraulický model vyhodnotí na danom stupni vážskej kaskády prevedie transformačný model na jalovo cez kanál.
Základnú inverznú rovnicu pre vyjadrenie prietoku z výkonu SRV môžeme zapísať v tvare:
|
[math]{{Q}_{SRV(krok)}}=\frac{{{P}_{SRV(krok)}}\cdot 1000}{g\cdot {{h}_{(krok)}}\cdot {{\eta }_{TG}}}[/math] |
(2.8) |
kde:
| PSRV | Elektrický výkon sekundárnej regulácie výkonu [MW]; |
| QSRV | Prietok vody pre sekundárnu reguláciu výkonu cez TG [[math]m^3.s^{-1}[/math]]; |
Ostatné členy rovnice sú totožné s členmi transformačnej rovnice 2.7.
Optimalizačný model
Nakoniec tejto kapitoly rozoberieme optimalizáciu použitú v hydromodeli, ktorej význam je aj v tom, že spája jednotlivé modely do jedného uceleného systému. Optimalizácia je základom pre hospodárne využívanie energetického potenciálu a hospodárneho navrhnutia nasadenia turbogenerátorov v najlepšie finančne ohodnotených hodinách dňa s ohľadom na dodržiavanie okrajových vodohospodárskych a energetických podmienok.
Vstupné parametre do optimalizačného modelu budú:
- Ocenenie DDZ;
- Prítok vody v jednotlivých medzipovodiach;
- Počiatočné a koncové hladiny na jednotlivých vodných nádržiach;
- Maximálne a minimálne prevádzkové hladiny nádrží a derivačných kanálov;
- Dostupnosť energetických zariadení (TG);
- Obmedzenia hladinovej a prietokovej prevádzky;
- Spôsob prevádzky (priebežná, špičková);
- Prevedenie jalových vôd cez kanálovú sústavu alebo hať do starého koryta rieky;
- Čas a prietok vody medzi posledným objektom VE danej SVK a vodnou nádržou a medzi stupňami;
- Mapa limitných prietokov.
Výstupom optimalizácie budú:
- Nasadenie prietokov cez energetické zariadenie podľa ocenenia DDZ;
- Energetické obmedzenia a navrhnutie prietoku jalových vôd (kanál, hať);
- Rozvrhnutie priebehov hladín vodných nádrží;
- Verifikácia a validácia hladinových režimov derivačných kanálov;
- Stanovenie ďalšej prevádzky v čase veľkých vôd.
Podstata optimalizačného modelu sa nachádza v procedúre Optimalizacia_Q_HH modulu StartOptimal, v ktorej sa nachádzajú algoritmy sledovania prekročenie HHmax., HHmin., dodržania využiteľného objemu vody počas dňa (posledný je rozdelený na dva, jednotlivo kontrolujú spotrebu väčšieho a menšieho objemu vody). Okrem spomenutých algoritmov sú pre optimalizáciu vytvorené podporné funkcie a procedúry, ktoré umožňujú kontroly a operácie nad veľkým množstvom údajov. Jedná sa o model, ktorý je riadený údajmi.
Vstupné parametre optimalizačného modelu
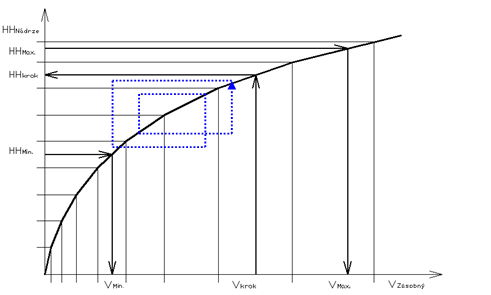
Ocenenie DDZ - Tento vstupný parameter vyjadruje výrobu v MWh a hodnotu veľkosti nasadenia v MW pre každú hodinu dňa. Takýmto spôsobom sú určené váhové hodnoty jednotlivých hodín, ktoré vyjadrujú veľkosť nasadenia energetických zariadení do prevádzky. Optimalizačný model v závislosti od ostatných vstupných podmienok navrhne nasadenie tak, aby sa čo najviac priblížil k hodnotám ocenenia DDZ. Štandardom je pri plánovaní dodržať hodnotu výroby s čo najlepším dosiahnutím tvaru výkonového nasadenia výrobných zariadení. Príklad takéhoto nasadenia DDZ je na obrázku 2.21. Zároveň je vidieť, v ktorých hodinách sú požiadavky na minimálne nasadenie a výkonové špičky počas celého dňa.
Prítok vody v jednotlivých medzipovodiach - Pre správnosť výpočtu sa musí objem vody, ktorý sa vlieva do vodnej nádrže rovnať objemu vody, ktorý sa z vodnej nádrže vylieva. Jediná možná nerovnosť môže nastať v prípade, keď sa nádrž plní alebo prázdni. Hydrologický model je nosičom všetkých informácii a väzieb medzi údajmi. Optimalizačný model tieto údaje spracováva tak, aby sa dosiahlo najlepšie možné riešenie úlohy s cieľom eliminovať stratu informácii o prietokoch. Úlohu optimalizuje, pokiaľ nenájde riešenie na prevedenie celého energeticky využiteľného prietoku bez zostatku. Ak sa mu tento prietok nepodarí previesť celý, zvyšok objemu vody ponechá v nádrži. V opačnom prípade, keď použije väčšie množstvo vody spotrebovaný objem sa prejaví na koncovej hladine v nádrži.
Počiatočné a koncové hladiny na jednotlivých vodných nádržiach - Prostredníctvom riadeného výpočtu sa z počiatočnej hladiny musíme priblížiť k plánovanej koncovej hladine vodnej nádrže daného dňa, prípadne ju dosiahnuť s čo najlepšie využitím prietoku hlavne cez energetickú časť. Koncová hladina sa v určitých prípadoch nedá dosiahnuť v presnej hodnote, ale podstata je priblížiť sa k nej čo najbližšie (Obr. 2.21). Situácia, kedy parameter koncovej hladiny nie je možné dodržať, je v čase veľmi nízkych denných prietokov cez SVK. Parametre minimálnych prevádzkových prietokov cez turbogenerátory sú v rozsahu desiatok m3.s-1, nie je teda možnosť jemného dolaďovania. Vzhľadom k tomu vyhodnotí model hladinu vyššiu alebo nižšiu, ako bola plánovaná. Na poslednom grafe obrázka 2.22 by sme mohli začať pochybovať o správnosti priebehu HH, je potrebné uvedomiť si, že optimalizačný model sa nielenže musí vyhnúť obmedzujúcim hladinám, ale čo je dôležité previesť potrebný objem vody na nasledujúci SVK a dodržať tak plánovanú koncovú hladinu. Pokiaľ počiatočná hladina nie je rovná koncovej plánovanej hladine, potom táto operácia znamená pre optimalizačný a hydrologický model zmenu v prietokovej bilancii jednotlivými SVK.
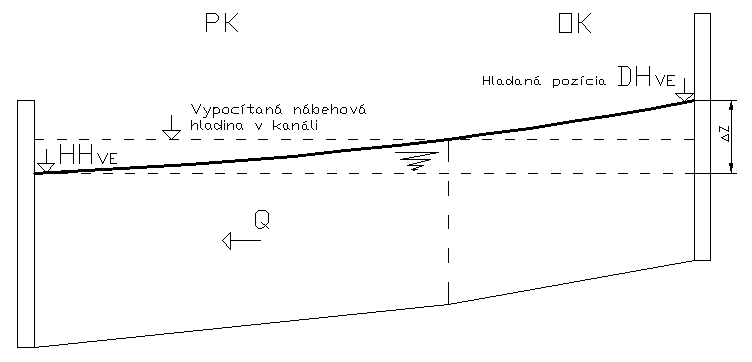
Maximálne a minimálne prevádzkové hladiny nádrží a derivačných kanálov - Optimalizácia pri svojom výpočte musí riešiť prekročenie obmedzujúcich prevádzkových hladín a v prípade, že sú mimo povolený rozsah, musí riadiť postup riešenia úlohy spôsobom, ktorý tento neželaný stav odvráti. Príklad je uvedený na obrázku 2.22, kde sú zobrazené tri situácie s rovnakými vstupmi okrem obmedzujúcich HH. Aj v takomto prípade je snaha optimalizačného modelu tvarovať nasadenie podľa ocenenia DDZ. V prípade kanálov je táto úloha riešená z časti optimalizáciou prostredníctvom máp limitných prietokov a z časti hydrologickým modelom. Hydrologický model v kanálovej časti obsahuje pre jednotlivé derivačné kanále objemové krivky, ktoré majú rozsah od HHmin. po HHmax. Hydrologická časť umožňuje meniť tieto obmedzujúce hladiny v nádržiach (pohyb HHmin. aj pohyb HHmax.), ale v kanáloch je umožnené meniť iba HLNábehovú a DHmax. pod objektom VE.
Optimalizačný model musí uvažovať s hladinovým režimom, či už v nádrži alebo v kanáli. V určitých prípadoch môže nastať obmedzenie do takej miery, že prietoky dosiahnu minimálnu hodnotu pre prevádzku TG na objektoch VE, prípadne úplné odstavenie VE z prevádzky. Na obrázku 2.23 je kanál medzi VE HR a VE MI. Pri väčších prietokoch model upravuje nábehovú hladinu tým, že začne plniť kanál potrebným množstvom vody. Pri hladinovom režime od 8:00 do 19:00, ktorý zobrazuje obrázok 2.24, je vidieť reakciu DHmax. na VE HR a zvýšenie prietoku modelom v ostatných hodinách dňa cez SVK HR-MI-PB. Rovnako ako v príklade TB (Obr. 2.22) všetky vstupy do modelu sú rovnaké, okrem obmedzenia DHmax.
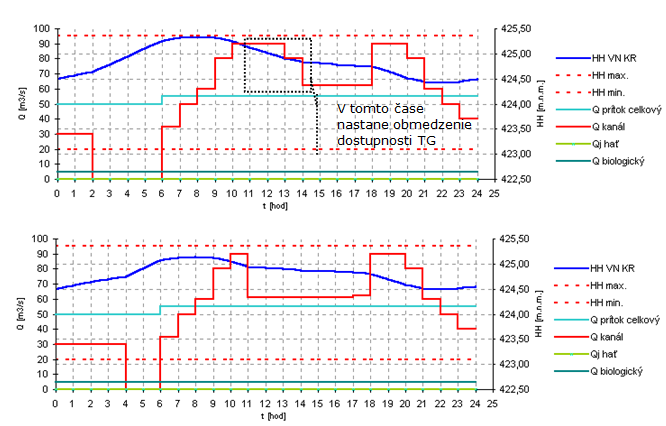
Dostupnosť energetických zariadení (TG) - V čase nedostupnosti energetického zariadenia na objekte VE sa môže plánovanie zamerať aj smerom celkového využitia objemu vody tak, aby nebolo zbytočne prevedené neenergeticky cez kanál, prípadne haťový objekt. Prevedenie vody nastane v čase dostupnosti TG, čím sa hospodárne využije hydroenergetický potenciál. Môžu nastať aj situácie, v ktorých by bez takéhoto prístupu nastalo plánované neenergetické prevedenie vody. Hydrologický model obsahuje informácie o možnostiach a na základe informácií, ktoré má k dispozícií, rieši optimalizačný model úlohu plánovania. Prioritne sa plánovanie zameriava na celkové prevedenie prietoku cez derivačný kanál, iba v špecifických prípadoch cez haťový objekt do starého koryta. No obrázku 2.25 je príklad nedostupnosti dvoch TG na VE KR v čase 11:00 až 14:00. Optimalizačný model preto časť výroby presunul do ranných hodín od 2:00 do 4:00.
Obmedzenia hladinovej a prietokovej prevádzky - Ako už bolo spomenuté v bode maximálnych a minimálnych prevádzkových hladín, v modeli je možnosť plánovania hladinových obmedzení. Hydrologický model obsahuje aj vstup pre čisto prietokové obmedzenie cez SVK. Optimalizačný model v prípade kombinácie jednotlivých hladinových a prietokových obmedzení, analyzuje najvýznamnejšie obmedzenie (to, ktoré viac ovplyvní prietok cez SVK) a to aplikuje vo výpočte úlohy. Predchádza sa tak aj spomínanej strate informácií o prietokoch. Ak by optimalizačný model nepočítal so spomínaným prípadom, potom výsledky, ktoré postúpi hydraulicko-transformačnému modelu sa nenávratne stratia. Ovplyvnil by sa výsledok skutočného nasadenia TG na VE, čo by spôsobilo v operatívnom riadení rozladenie prevádzky zdrojov a nutnosť korekcie výkonov zdrojmi navzájom.
Spôsob prevádzky - Spôsob prevádzky TG na objektoch VE môže byť špičkový, čo znamená minimalizovanie výroby prípadne úplné odstavenie v čase, kedy je prevádzka menej finančne ekonomická (nočné hodiny) a maximalizovanie výroby v čase ekonomicky výhodnejšej prevádzky (denné hodiny). Takáto prevádzka je hlavne v čase bežných prítokov, pri ktorých je možnosť odľahčiť výrobu na TG a akumulovať vodu do voľného objemu vodnej nádrže. Vážska kaskáda má svoje najužšie miesto na prevedenie vody v úseku VE LA až VE HS, čo je približne 180 m3.s-1, kde väčšinu roka prevláda pološpičková a priebežná prevádzka. Je to z dôvodu prípravy voľného objemu pre špičkovú prevádzku vyšších stupňov, ako napr. SVK HR-MI-PB s veľkým prietokom 399 m3.s-1.
Prevedenie jalových vôd cez kanálovú sústavu alebo hať do starého koryta rieky - Informácia pre výber jednej z možností je v hydrologickom modeli. Spomínali sme ju aj v bode dostupnosti energetických zariadení a jej celkový význam pri zakázaní prepúšťať Qj do kanála spôsobuje, že optimalizačný model hľadá vždy riešenie úlohy s minimálnym alebo s nulovým prepúšťaním Qj. Prioritne je maximum využiteľného objemu prevedené energeticky.
Čas a prietok vody medzi posledným objektom SVK a vodnou nádržou a medzi stupňami - K riešeniu tejto úlohy využíva optimalizácia model pre výpočet času prítoku a transformáciu prietokovej vlny z posledného objektu VE príslušnej SVK, ale aj z hate cez pôvodné koryto Váhu. Tento faktor ovplyvňuje nasadenie energetických zariadení do prevádzky a v neposlednom rade je nositeľom dôležitej informácie pri zmenách odtokov z vrcholových nádrží pre plánovanie výroby na D+1. Rovnako aj pri veľkých vodách, kedy sa značný objem prevádza haťou do koryta Váhu, čo po určitom čase spôsobí vzdutie dolných hladín posledných objektov VE príslušnej SVK a môže tak prípadne obmedziť prevádzku celej kaskády.
Mapa limitných prietokov - Optimalizačný algoritmus je tak dobre informovaný o riešení danej úlohy, ako sme mu schopní tieto informácie poskytnúť. V našom prípade modelu optimalizácie dáme informácie, ktoré umožnia ešte v čase pred odoslaním výsledkov na hydraulicko-transformačný model verifikovať a validovať hraničné obmedzenia prietokov cez energetické zariadenie VE. Aby bol výpočet optimalizačného modelu bez chýb je nevyhnutne potrebné, aby vedel o hraničných obmedzeniach jednotlivých TG a obmedzeniach derivačných kanálov. Bolo potrebné vyhodnotiť a pripraviť v hydraulicko-transformačnom module mapy:
- Mapy maximálneho prietoku cez energetickú časť vodných diel
- Obsahujú prietoky od veľkých vôd až po bežnú prevádzku a každý prietok je vyhodnotený k hladinám v nádrži s rastrom 0,05 m od HHmax. po HHmin. Zaznamenané sú aj prietokové prechody pri spomínaných hladinách medzi TG. Rozsah maximálneho prietoku cez VD je ukončený pri hodnotách, keď nastáva úplné odstavenie energetickej časti z dôvodu nedodržania prevádzkových obmedzení.
- Mapy maximálneho prietoku cez jednotlivé kanále
- Každý derivačný kanál je vyhodnotený samostatne. Týmto spôsobom máme možnosť pracovať s HLNábehovou a DHmax. vyššie postaveného objektu na derivačnom kanáli. V mapách limitných prietokov sú zaznamenané pozície hladín a k nim stanovené maximálne prietokové obmedzenia kanála. V hydromodelovaní je tak umožnené plánovať aj hladinové režimy v tejto časti.
- Mapy minimálneho prietoku cez jednotlivé VE
- Minimálne obmedzenia každej VE je súčasťou máp limitných prietokov a slúži na stanovenie minimálneho prietoku cez objekty VE daného SVK. Je to z dôvodu, aby nebol podkročený minimálny prietok jedeného z objektov VE v priebehu hydromodelovania, čím by hydraulicko-transformačný model vylúčil tento objekt z prevádzky. Dôležité je to pri plánovaní vody a výroby z nej.
Pre optimalizáciu sú mapy zdrojom informácií, pomocou ktorých v predstihu dokáže predikovať situáciu a správne plánovať vodu tak, aby nedochádzalo k strate informácií o vode a o nasadenom výkone objektov VE, ako aj o celkovej práci vážskej kaskády. Významne sa prostredníctvom máp ovplyvní čas výpočtu riešenej úlohy a v prípadoch veľkých vôd aj jej konečnosť a riešiteľnosť.
Výstupné parametre optimalizačného modelu
Nasadenie prietokov cez energetické zariadenie podľa ocenenia DDZ Stanovenie veľkosti prietoku vody cez objekty VE a zároveň nasadenie počtu TG do prevádzky plánuje optimalizačný model autonómne. Počas mimoriadnych manipulácii je však umožnené užívateľovi ovplyvňovať túto autonómnosť pomocou vstupov na to určených (maximálny a minimálny prietok; hladinový režim - kanál a vodná nádrž; dostupnosť TG; ovplyvnenie spracovania vody pred a po čase, v ktorom je TG mimo prevádzky atď.).
Veľkosť prietoku v jednotlivých hodinách dňa je určená výrazom: VZOREC (2.9)
POKRACOVANIE VZORCA
Priemerná hodnota denného prietoku cez SVK sa vypočíta zo zložiek:
- Prítok z medzipovodia;
- Prítok z vyššie postaveného objektu VE;
- Prítok jalovej vody zo starého koryta;
- Odtok biologický do starého koryta;
- Pohyb hladiny v nádrži.
Zároveň musia byť k dispozícii informácie o prítoku vody z D-1, v opačnom prípade nastáva chyba výpočtu priemernej hodnoty odtoku vody z SVK. Vypočítaný prietok každej hodiny dňa nie je počítaný priamo z rovnice 2.9, ale týmto spôsobom je navrhnutý. Prietoky jednotlivých hodín sú korigované optimalizačným modelom v závislosti od ďalších vstupov a modelovanej situácie.
Energetické obmedzenia a navrhnutie prietoku jalových vôd - Optimalizačný model vo svojom výstupe delí vodu na spracovanie cez SVK a na vodu cez hať, keď sú kapacity energetickej časti vyčerpané. Jalové vody do hatí sú prepúšťané priebežne podľa stanoveného denného prietoku VD.
Rozvrhnutie priebehov hladín vodných nádrží - Pri vyhodnocovaní nastavených hodinových prietokov cez SVK optimalizačný model využíva model hydraulickej časti pre vodné nádrže. Je to jeden zo spôsobov akým overuje nasadenie prednastaveného prietoku spomenutého v odstavci pre nasadenie prietokov podľa ocenenia DDZ.
Verifikácia a validácia hladinových režimov derivačných kanálov - Ak nastane situácia modelovať hladinový režim v derivačných kanáloch, optimalizačný model vyhodnotí jej riešiteľnosť. Pokiaľ nie je dostatok vody na prevádzku SVK, model začne upravovať interval plnenia alebo prázdnenia kanála, prípadne interval ponechá pôvodný, ale upraví cieľovú hladinu v kanáli.
Na obrázku 2.26 je priebeh prevádzky VE LA a VE IL bez úpravy nábehovej hladiny. Na poslednom grafe obrázku 2.26 je priebeh prevádzky po úprave nábehovej hladiny na VE IL, čo spôsobí aj zmenu prietokovej bilancie cez objekty VE.
Stanovenie ďalšej prevádzky v čase veľkých vôd - Pár krát do roka je potrebné riešiť plánovanie veľkých vôd. Ako už bolo spomenuté v predchádzajúcom bode mapy limitných prietokov, optimalizačný model s takouto možnosťou počíta. Vodu, ktorú posiela model haťou po vymodelovaní jedného SVK transformuje prostredníctvom modelu dotoku vody a opätovne prehodnocuje, opakovane počíta nastavenie vody na kanál a hať, pokiaľ sa obmedzenia prietoku na objektoch VE neustália. Pri väčších prietokoch nastáva aj odstavenie z prevádzky a celý prietok je prevedený haťou. Na nasledujúcom obrázku 2.27 je umelo nastavený veľmi náhly vzostup vody na objekte VN TB vypočítaný z prepadu jalovej vody cez hať DK od polnoci cez staré koryto Váhu. Prítok dorazil o 9:00 a prevádzku celého SVK KO-NM-HS začal ovplyvňovať o 18:00, kedy DH na VE HS začala dosahovať maximálnu prevádzkovú hladinu. Postupné znižovanie prietoku cez kanál sa optimalizačný model snažil udržať kaskádu v prevádzke, až kým nenastalo vzdutie DH HS z jalovej vody cez staré koryto do takej miery, že model kaskádu odstavil z prevádzky.