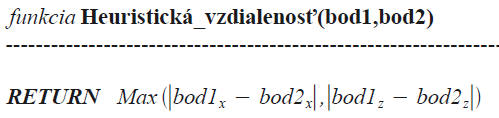Multi-analýza a syntéza simulačného programu: Rozdiel medzi revíziami

Z Kiwiki
Skočit na navigaci Skočit na vyhledávání
 
(Jedna medziľahlá úprava od rovnakého používateľa nie je zobrazená.)
Riadok 162: Riadok 162:
 
###bod terénu
 
###bod terénu
 
###*priechodný - vyznačuje sa cenou cesty do cieľa, cenou cesty do cieľa cez najlepšieho suseda, vlastnou cenou >= 0 (výškou)
 
###*priechodný - vyznačuje sa cenou cesty do cieľa, cenou cesty do cieľa cez najlepšieho suseda, vlastnou cenou >= 0 (výškou)
−
###*nepriechodný – prekážka, vyznačuje sa cenou cesty do cieľa = ꝏ, cenou cesty do cieľa cez najlepšieho suseda = ꝏ, vlastnou cenou < 0
+
###*nepriechodný – prekážka, vyznačuje sa cenou cesty do cieľa = <math>\infty </math>, cenou cesty do cieľa cez najlepšieho suseda = <math>\infty </math>, vlastnou cenou < 0
 
###**prekážky vyplývajúce z ohraničenia terénu vzhľadom na vozidlo
 
###**prekážky vyplývajúce z ohraničenia terénu vzhľadom na vozidlo
 
###**prekážky vyplývajúce z max. rozdielu dvoch po sebe idúcich výšok ↔ vlastných cien (určované užívateľom)
 
###**prekážky vyplývajúce z max. rozdielu dvoch po sebe idúcich výšok ↔ vlastných cien (určované užívateľom)
Riadok 367: Riadok 367:
 
Pyramída pohľadu je v skutočnosti pyramídou s odpíleným vrcholom. Takáto pyramída pozostáva zo 6 rovín, a to z blízkej, vzdialenej, ľavej, pravej, hornej a dolnej. Roviny sú zadefinované tak, že ich normálové vektory smerujú do vnútra pyramídy.
 
Pyramída pohľadu je v skutočnosti pyramídou s odpíleným vrcholom. Takáto pyramída pozostáva zo 6 rovín, a to z blízkej, vzdialenej, ľavej, pravej, hornej a dolnej. Roviny sú zadefinované tak, že ich normálové vektory smerujú do vnútra pyramídy.
  
−
[[Súbor:.png|center|framed|Obr. ]]
+
[[Súbor:Znázornenie bodov pyramídy perspektívneho pohľadu (36).png|center|framed|Obr. 36 Znázornenie bodov pyramídy perspektívneho pohľadu]]
−
[[Súbor:.png|center|framed|Obr. ]]
+
 
 +
Zadefinujeme (Obrázok 36/37):
 +
*P=pozíciakamery
 +
* <math>vyska_1</math>=výška blízkej orezávacej roviny
 +
* <math>sirka_1</math>=šírka blízkej orezávacej roviny
 +
* <math>vzdialenost_2</math>=vzdialenosť od kamery ku vzdialenej orezávacej rovine
 +
*<math>vyska_2</math>=výška vzdialenej orezávacej roviny
 +
*<math>sirka_2</math>=šírka vzdialenej orezávacej roviny
 +
*d=normalizovaný vektor smeru pozorovania
 +
*up=normalizovaný normálový vektor hornej plochy kamery
 +
*vr=normalizovaný vektor smerujúci vpravo
 +
 
 +
Ak zistíme polohu bodu S(Obrázok 37), ľahko určíme ostatné body. Bod ''S'' slúži len ako nástroj na zistenie bodov 5, 6, 7, 8 (Obrázok 36).
 +
 
 +
Výpočet pre bod S (Obrázok 37):
 +
 
 +
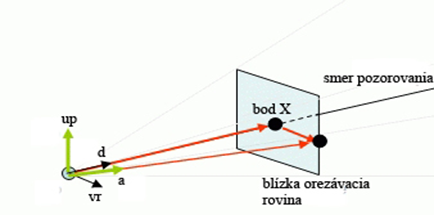
[[Súbor:Zobrazenie pyramídy perspektívneho  pohľadu s vektormi kamery (37).png|center|framed|Obr. 37 Zobrazenie pyramídy perspektívneho  pohľadu s vektormi kamery]]
 +
 
 +
<math>S=P+d*vzdialenost_2</math>
 +
 
 +
Výpočet pre body 5, 6, 7, 8 (Obrázok 36):
 +
 
 +
<math>bod_5=S+(up*vyska_2/2)–(vr*sirka_2/2)</math>
 +
 
 +
<math>bod_6=S-(up*vyska_2/2)–(vr*sirka_2/2)</math>
 +
 
 +
<math>bod_7=S-(up*vyska_2/2)–(vr*sirka_2/2)</math>
 +
 
 +
<math>bod_8=S+(up*vyska_2/2)–(vr*sirka_2/2)</math>
 +
 
 +
Analogicky sa vykoná výpočet pre body 1, 2, 3, 4 (Obrázok 36):
 +
 
 +
<math>S=P+d*vzdialenost_1</math>
 +
 
 +
 
 +
<math>bod_1=S+(up*vyska_1/2)–(vr*sirka_1/2)</math>
 +
 
 +
<math>bod_2=S-(up*vyska_1/2)–(vr*sirka_1/2)</math>
 +
 
 +
<math>bod_3=S-(up*vyska_1/2)–(vr*sirka_1/2)</math>
 +
 
 +
<math>bod_4=S+(up*vyska_1/2)–(vr*sirka_1/2)</math>
 +
 
 +
Blízka orezávacia rovina môže byť definovaná vektorom dako normálou a bodom Xako bodom v tejto rovine. A vektor ''-d'' môžeme použiť ako normálu pre vzdialenú orezávaciu rovinu a bod v tejto rovine je bod S. Musíme si uvedomiť, že bod P je výnimočný bod, je to pozícia kamery a zároveň leží aj v ostatných orezávacích rovinách (ľavá, pravá, horná, spodná).
 +
 
 +
[[Súbor:Postup výpočtu normály pre pravú orezávaciu rovinu (38).png|center|framed|Obr. 38 Postup výpočtu normály pre pravú orezávaciu rovinu]]
 +
 
 +
Ukážkový výpočet normály pre pravú orezávaciu rovinu (Obrázok 38): Vypočítame <math>a=d*vzdialenost_1+vr*sirka_1/2</math>, vektor aje v podstate vektorový súčet vektorov <math>d*vzdialenost_1</math> a vektora <math>vr*sirka_1/2</math>. Pri tomto vektore nás nezaujíma veľkosť, ale len smer, normalizujeme ho. Naša hľadaná normála je <math>normala_{pravej roviny} =up × a</math> jednoducho odvodená z definície vektorového súčinu.
 +
 
 +
==Vykresľovanie terénu==
 +
Vykresľovanie terénu znamená vykresliť všetky viditeľné podpriestory, ktoré úspešne prešli testom (Pseudoalgoritmus 18, príloha B). Test sa vykoná pre všetky podpriestory. Uskutočňuje sa dosadením každého z 8 bodov (transformovaných aktuálnou MP maticou,<math>bo{{d}_{transf}}=MP*bod</math>) ohraničenia priestoru do každej zo 6 rovín pyramídy pohľadu. Ak podpriestor leží celý v pyramíde musí mať každý bod podpriestoru kladnú vzdialenosť od každej roviny, pretože jedine vtedy sa nachádza v smere normál rovín, ktoré všetky smerujú dovnútra pyramídy.
 +
 
 +
Ak priestor leží čiastočne v pyramíde,  znamená to, že aspoň jeden bod podpriestoru má kladnú vzdialenosť od každej roviny pyramídy. Toto sú dva prípady kedy musíme podpriestor terénu vykresliť.
 +
 
 +
Po teste viditeľnosti (Pseudoalgoritmus 18, príloha B) nasleduje cyklus, ktorý podľa výsledku testu vykreslí alebo nevykreslí daný priestor. Vykresľovanie prebieha pomocou polí vrcholov s multitextúrovaním a trianguláciou. Každý riadok terénu začína troma bodmi trojuholníka, a potom pokračuje pridávaním jedného bodu s ohľadom na vinutie polygónu.
 +
 
 +
Technológia polí vrcholov výrazne urýchľuje aplikáciu, pretože pre takýto spôsob vykresľovania primitív stačí zadať len ukazovateľ na dané pole súradníc bodov a počet prvkov poľa. Vďaka tomu prechádzanie cyklami už nemusí byť uskutočňované pre každý bod poľa, ale len ako prechod na nový riadok kvôli triangulácii.
 +
 
 +
Kamerový systém
 +
Kameru v simulácii „vytváram” volaním funkcie gluLookAt. Funkcia gluLookAt vytvára pozorovateľskú transformáciu vo forme modelovacej matice. Táto matica nám transformuje objekty v scéne do pozorovateľského priestoru.
 +
Dôležité parametre kamerového systému, ktoré som zostrojil a programovo implementoval sú smerové vektory <math>vd=[v{{d}_{x}},v{{d}_{y}},v{{d}_{z}}]</math> (smer pozorovania), <math>vu=[v{{u}_{x}},v{{u}_{y}},v{{u}_{z}}]</math>(normálový vektor kolmý na hornú plochu kamery), <math>r=[v{{r}_{x}},v{{r}_{y}},v{{r}_{z}}]</math>(pravý vektor) a bod <math>vp=[v{{p}_{x}},v{{p}_{y}},v{{p}_{z}}]</math>(bod odkiaľ sa pozeráme, poloha kamery).
 +
 
 +
Funkciu ''gluLookAt'' môžeme nahradiť (vysvetliť) aj vlastnou konštrukciou príkazov, pričom musíme poznať <math>vp=[v{{p}_{x}},v{{p}_{y}},v{{p}_{z}}]</math>, bod na ktorý sa pozeráme <math>centrum=[v{{p}_{x}}+v{{d}_{x}},v{{p}_{y}}+v{{d}_{y}},v{{p}_{z}}+v{{d}_{z}}]</math> a <math>vu=[v{{u}_{x}},v{{u}_{y}},v{{u}_{z}}]</math>, ktorý normalizujeme.
 +
 
 +
Z týchto parametrov odvodíme jednotkový vektor  <math>d=[centru{{m}_{x}}-v{{p}_{x}},centru{{m}_{y}}-v{{p}_{y}},centru{{m}_{z}}-v{{p}_{z}}]</math>. Potom zistíme hodnotu vektora vpravo z vektorového súčinu vr=vd×vu, normalizujeme ho a vypočítame aj nový jednotkový normálový vektor kamery pomocou vu=vr×vd.
 +
Zistili sme ako vyzerá aktuálny  súradnicový systém kamery. Vytvoríme transformačnú maticu 3x3 (modelovacia transformácia), ktorá je v podstate iverznou maticou k matici súradnicového systému kamery (stačí vytvoriť transponovanú maticu, pretože sa jedná o ortonormálny systém)  a s doplnením na homogénnu maticu (4x4) :
 +
 
 +
<math>F=\begin{matrix}
 +
  v{{r}_{x}} & v{{r}_{y}} & v{{r}_{z}} & 0  \\
 +
  u{{p}_{x}} & u{{p}_{y}} & u{{p}_{z}} & 0  \\
 +
  -v{{d}_{x}} & -v{{d}_{y}} & -v{{d}_{z}} & 0  \\
 +
  0 & 0 & 0 & 1  \\
 +
\end{matrix}</math>
 +
 
 +
Potrebujeme ešte vytvoriť transformačnú maticu posunu T, ktorá zabezpečí posun (inverzne ku kamere) o opačné hodnoty ako sú súradnice polohy kamery v globálnom súradnicovom systéme, aby bod, na ktorý sa pozeráme bol počiatok. Výsledná modelovacia matica, ktorá reprezentuje pozorovateľskú transformáciu (totožnú s ''gluLookAt'') bude F.T.
 +
 
 +
===Lietajúca kamera===
 +
Interakcia pre tento druh kamery je vyriešená pomocou kláves 'W','A', 'S', 'D', 'R', 'E' a pohybov kurzoru myši. Pri interakcii s jednou z kláves 'W', 'A', 'S', 'D'  automaticky nastane posunutie v smere niektorej osi kamery (v smere/protismere vr a vd). Deje sa to jednoduchým pričítaním časti vektora vd alebo vr k bodu polohy kamery vp. Časť vektora získame vynásobením jednotkového vektora vd premennou <math>posun_z</math> alebo vr premennou <math>posun_x</math>.
 +
Veľkosť týchto premenných sa určuje po každom stlačení príslušnej klávesy priradením aktuálnej veľkosti posunu pomocou konštanty <math>velkost_{posunu}</math>.Veľkosť konštanty <math>velkost_{posunu}</math> zmeníme klávesami 'R', 'E'. Potom pre premenné posunov a pozíciu kamery platí (v danom poradí):
 +
 
 +
 
 +
<math>\begin{align}
 +
  & posu{{n}_{x}}=\pm velkos{{t}_{posunu}} \\
 +
& posu{{n}_{z}}=\pm velkos{{t}_{posunu}} \\
 +
& vp=vp+posu{{n}_{x}}*vr+posu{{n}_{z}}*vd \\
 +
\end{align}</math>
 +
 
 +
Po pričítaní ku aktuálnej pozícii kamery sa pozícia kamery vp posunie o nejaký kúsok v smere/protismere vd alebo vr. Podobne funguje aj interakcia s myšou. Zmena smeru pozorovania ''vd'' začína  výpočtom miery zmeny posunu vzhľadom na polohu kurzoru myši na  stred obrazovky, platí :
 +
 
 +
 
 +
<math>\begin{align}
 +
  & mier{{a}_{x}}=(kurzo{{r}_{x}}-sirka\_okna*0.5)*0.005 \\
 +
& mier{{a}_{y}}=(vyska\_okna*0.5-kurzo{{r}_{y}})*0.005 \\
 +
\end{align}</math>
 +
 
 +
Pre nový smer pozorovania vd a vektor vpravo vr  platí (v danom poradí):
 +
 
 +
<math>\begin{align}
 +
  & vr=\frac{vd\times vu}{\left| vd\times vu \right|} \\
 +
& vd=vd+mier{{a}_{y}}*vu+mier{{a}_{x}}*vr \\
 +
& vd=\frac{vd}{vd} \\
 +
\end{align}</math>
 +
 
 +
Vzdialenosť k bodu, na ktorý sa pozeráme vd+vpje z bodu pozorovania vp vždy 1, pretože vd je jednotkový vektor. Po každej takejto transformácii treba nastaviť polohu kurzoru myši na stred obrazovky a premenné posunu nulovať:
 +
 
 +
<math>\begin{align}
 +
  & kurzo{{r}_{x}}=\check{s}\acute{i}rka\_okna/2 \\
 +
& kurzo{{r}_{y}}=v\acute{y}\check{s}ka\_okna/2 \\
 +
& posu{{n}_{x}}=0 \\
 +
& posu{{n}_{z}}=0 \\
 +
\end{align}</math>
 +
 
 +
 
 +
==Prezentačná kamera==
 +
Smer pozorovania prezentačnej kamery je vždy smerom do polohy ťažiska vozidla. Kamera automaticky nasleduje vozidlo z premenlivej  výšky vypočítanej z polohy kamery v teréne (i mimo terénu). Poloha kamery na osiach X, Z je ľubovoľná. Pred prechodom do režimu prezentačnej kamery môžeme pomocou lietajúcej kamery  vybrať ľubovoľnú polohu na osiach X, Z. Najprv vypočítame aktuálny vektor kamery ukazujúci vpravo vr:
 +
 
 +
* <math>posun_x</math>=budúci posun ťažiska na osi X
 +
* <math>posun_z</math>=budúci posun ťažiska na osi Z
 +
* ''vd''=smer pozorovania
 +
* ''vu''=vektor kolmý na vrchnú plochu kamery
 +
* vr=vd×vu
 +
 
 +
Ďalej potrebujeme vyjadriť posun polohy kamery vpv globálnom súradnicovom systéme (GSS) na osiach X, Z a aj polohu bodu pozorovania"bod_pozorovania"  (budúce ťažisko vyjadrené v súradnicovom systéme terénu)  v GSS:
 +
 
 +
posun_terénu=[x,y,z], určuje polohu terénu v GSS
 +
 
 +
*<math>vp_x=vp_x+posun_x</math>
 +
*<math>vp_z=vp_z+posun_z</math>
 +
* <math>{bod pozorovania}_{x}={bod pozorovania}_{x}+{posun terénu}_{x}</math>
 +
* <math>{bod pozorovania}_{y}={bod pozorovania}_{y}+{posun terénu}_{y}</math>
 +
* <math>{bod pozorovania}_{z}={bod pozorovania}_{z}+{posun terénu}_{z}</math>
 +
 
 +
Pre správny výpočet výšky kamery v teréne musíme poznať aj polohu kamery v súradnicovom systéme terénu (TSS)  vplna osiach X, Z:
 +
 
 +
* <math>vpl_x=vp_x- {posun terénu}_{x}</math>
 +
* <math>vpl_z=vp_z- {posun terénu}_{z}</math>
 +
 
 +
Reálne hodnoty súradníc X, Z (s desatinnou čiarkou) prepočítanej polohy kamery ''vpl'' zaokrúhlime k najbližšej celočíselnej hodnote.
 +
Ak tieto súradnice X, Z vektora vplurčujú polohu kamery mimo terénu nahradíme ich súradnicami X, Z najbližšieho celočíselneho bodu terénu. Najbližší bod uprednostňujem aj z dôvodu plynulého prechodu kamery z oblasti mimo terénu na terén.
 +
 
 +
Výsledné celočíselné hodnoty môžeme využiť ako indexy dvojrozmerného poľa prevýšková"_" mapa(výšková mapa), pričom hodnota tohto poľa s týmito indexami (X, Z) predstavuje výšku bodu v teréne na týchto súradniciach X, Z. Potom pre súradnicu Y (výška) polohy  kamery vpa výsledný smer pozorovania vdplatí (v danom poradí):
 +
 
 +
<math>\begin{align}
 +
  & v{{p}_{y}}=v{{p}_{y}}+vyskova\_mapa[vp{{l}_{z}}][vp{{l}_{x}}]+30 \\
 +
& v{{d}_{x}}=bod\_pozorovani{{a}_{x}}-v{{p}_{x}} \\
 +
& v{{d}_{y}}=bod\_pozorovani{{a}_{y}}-v{{p}_{y}} \\
 +
& v{{d}_{z}}=bod\_pozorovani{{a}_{z}}-v{{p}_{z}} \\
 +
\end{align}</math>
 +
 
 +
 
 +
===Kamera za vozidlom===
 +
Výpočet začína vyjadrením polohy kamery ''vpl'' vzhľadom na ťažisko vozidla  "bod_pozorovania" v súradnicovom systéme terénu (TSS), ktoré je zároveň bodom pozorovania tejto kamery (v poradí):
 +
 
 +
* ''polomer_vozidla''=určuje užívateľ v konfig.súbore vozidla
 +
* T=4x4 matica,posun o súradnice X,Z ťažiska vyjadreného v SS terénu
 +
* R=4x4 matica,rotácia o uhol pootočenia kolies vozidla"
 +
* <math>vpl_x</math>=-polomer_vozidla-40
 +
* <math>vpl_y=0</math>
 +
* <math>vpl_z=0</math>
 +
Nasleduje transformácia maticami:
 +
 
 +
<math>vpl=T.R.vpl</math>
 +
 
 +
Ďalej potrebujeme vyjadriť polohu kamery v globálnom súradnicovom systéme (GSS) ako vpa polohu ťažiska "bod_pozorovania" (vyjadrené v TSS) v GSS:
 +
 
 +
* posun_terénu="[x,y,z],určuje polohu terénu v GSS
 +
* <math>vp_x=vpl_x+{posun terénu}_{x}</math>
 +
* <math>vp_y=vpl_y+{posun terénu}_{y}</math>
 +
* <math>vp_z=vpl_z+{posun terénu}_{z}</math>
 +
* <math>{bod pozorovania}_{x}={bod pozorovania}_{x}+{posun terénu}_{x}</math>
 +
* <math>{bod pozorovania}_{y}={bod pozorovania}_{y}+{posun terénu}_{y}</math>
 +
* <math>{bod pozorovania}_{z}={bod pozorovania}_{z}+{posun terénu}_{z}</math>
 +
 
 +
Reálne hodnoty súradníc X, Z (s desatinnou čiarkou) polohy kamery vplvyjadrenej v TSS zaokrúhlime k najbližšej celočíselnej hodnote. Ak tieto súradnice X, Z vektora vplurčujú polohu kamery mimo terénu nahradíme ich súradnicami X, Z najbližšieho celočíselneho bodu terénu. Najbližší bod upredňostňujem aj z dôvodu plynulého prechodu kamery z oblasti mimo terénu na terén.
 +
 
 +
Výsledné celočíselné hodnoty môžeme využiť ako indexy dvojrozmerného poľa prevýšková"_" mapa(výšková mapa), pričom hodnota tohto poľa s týmito indexami (X, Z) predstavuje výšku bodu v teréne na týchto súradniciach X, Z. Potom pre súradnicu Y (výška) polohy  kamery ''vpv'' GSS a výsledný smer pozorovania ''vd'' platí (v danom poradí):
 +
 
 +
<math>\begin{align}
 +
  & v{{p}_{y}}=v{{p}_{y}}+vyskova\_mapa[vp{{l}_{z}}][vp{{l}_{x}}]+30 \\
 +
& v{{d}_{x}}=bod\_pozorovani{{a}_{x}}-v{{p}_{x}} \\
 +
& v{{d}_{y}}=bod\_pozorovani{{a}_{y}}-v{{p}_{y}} \\
 +
& v{{d}_{z}}=bod\_pozorovani{{a}_{z}}-v{{p}_{z}} \\
 +
\end{align}</math>
 +
 
 +
===Rotačná kamera===
 +
Kroky potrebné k vytvoreniu a fungovaniu rotačnej kamery sú skoro totožné s kamerou za vozidlom. Jediný rozdiel je v spôsobe určovania natočenia polohy kamery vzhľadom na ťažisko vozidla.
 +
 
 +
Výpočet začína vyjadrením polohy kamery vplvzhľadom na ťažisko vozidla  "bod_pozorovania" v súradnicovom systéme terénu (TSS), ktoré je zároveň bodom pozorovania tejto kamery (v nasledujúcom poradí):
 +
 
 +
* polomer_vozidla=určuje užívateľ v konfig.súbore vozidla
 +
* T=4x4 matica,posun o súradnice X,Z ťažiska vyjadreného v SS terénu
 +
* R=4x4 matica,rotácia o uhol rotačný_uhol
 +
 
 +
<math>\begin{align}
 +
  & IF(++rotacny\_uhol\equiv 360{}^\circ ) \\
 +
& \ \ \ \ rota\check{c}n\acute{y}\_uhol\leftarrow 1{}^\circ  \\
 +
& vp{{l}_{x}}=-polomer\_vozidla-60 \\
 +
& vp{{l}_{y}}=0 \\
 +
& vp{{l}_{z}}=0 \\
 +
\end{align}</math>
 +
 
 +
Nasleduje transformácia maticami:
 +
 
 +
<math>vpl=T.R.vpl</math>
 +
 
 +
Ďalej potrebujeme vyjadriť polohu kamery v globálnom súradnicovom systéme (GSS) ako vpa polohu ťažiska "bod_pozorovania" taktiež v GSS:
 +
 
 +
<math>\begin{align}
 +
  & posun\_terenu=[x,y,z]\text{, }\!\!~\!\!\text{ urcuje }\!\!~\!\!\text{ polohu }\!\!~\!\!\text{ terenu }\!\!~\!\!\text{ v }\!\!~\!\!\text{ GSS} \\
 +
& v{{p}_{x}}=vp{{l}_{x}}+posun\_teren{{u}_{x}} \\
 +
& v{{p}_{y}}=vp{{l}_{y}}+posun\_teren{{u}_{y}} \\
 +
& v{{p}_{z}}=vp{{l}_{z}}+posun\_teren{{u}_{z}} \\
 +
& bod\_pozorovani{{a}_{x}}=bod\_pozorovani{{a}_{x}}+posun\_teren{{u}_{x}} \\
 +
& bod\_pozorovani{{a}_{y}}=bod\_pozorovani{{a}_{y}}+posun\_teren{{u}_{x}} \\
 +
& bod\_pozorovani{{a}_{z}}=bod\_pozorovani{{a}_{z}}+posun\_teren{{u}_{x}} \\
 +
\end{align}</math>
 +
 
 +
Reálne hodnoty súradníc X, Z (s desatinnou čiarkou) polohy kamery ''vpl'' vyjadrenej v TSS zaokrúhlime k najbližšej celočíselnej hodnote. Ak tieto súradnice X, Z vektora vplurčujú polohu kamery mimo terénu nahradíme ich súradnicami X, Z najbližšieho celočíselneho bodu terénu. Najbližší bod upredňostňujem aj z dôvodu plynulého prechodu kamery z oblasti mimo terénu na terén.
 +
 
 +
Výsledné celočíselné hodnoty môžeme využiť ako indexy dvojrozmerného poľa pre výšková_mapa (výšková mapa), pričom hodnota tohto poľa s týmito indexami (X, Z) predstavuje výšku bodu v teréne na týchto súradniciach X, Z. Potom pre súradnicu Y (výška) polohy  kamery vpv GSS a výsledný smer pozorovania vdplatí (v danom poradí):
 +
 
 +
<math>\begin{align}
 +
  & v{{p}_{y}}=v{{p}_{y}}+vyskova\_mapa[vp{{l}_{z}}][vp{{l}_{x}}]+30 \\
 +
& v{{d}_{x}}=bod\_pozorovani{{a}_{x}}-v{{p}_{x}} \\
 +
& v{{d}_{y}}=bod\_pozorovani{{a}_{y}}-v{{p}_{y}} \\
 +
& v{{d}_{z}}=bod\_pozorovani{{a}_{z}}-v{{p}_{z}} \\
 +
\end{align}</math>
 +
 
 +
=Záver=
 +
Úlohou tejto práce bolo vytvoriť multi-platformné simulačné prostredie pre pohyb vozidla v závislosti od užívateľských parametrov. Náročnosť témy ma  donútila venovať sa štúdiu rôznych oblastí potrebných pre teoretické základy k praktickej realizácii. Boli to predovšetkým matematika, počítačová grafika, umelá inteligencia, knižnice v jazyku C++, pokročilé možnosti programovania v C++ a spôsoby implementácie modulov jazyka Python v C++. Z tohto dôvodu som rozdelil diplomovú prácu na dve hlavné časti, teoretickú a praktickú. Významné miesto v prvej časti zaberá knižnica OpenGL, SDL, Libconfig a inkrementálno-heuristický  algoritmus D* Lite.
 +
 
 +
V praktickej časti som sa zaoberal predovšetkým vlastnými návrhmi algoritmov a iných riešení, ich implementáciami a vlastnou implementáciou i úpravami finálnej verzie algoritmu  D* Lite. Vytvoril som vlastný konfiguračný a parsovací systém pre konštrukciu užívateľského menu. Užívateľ podľa jasných pravidiel (opísaných v práci) dokáže skonštruovať ľubovoľné, vlastné obrázkové menu priamo zápisom do konfiguračného súboru. Existujúce menu s vyplneným konfiguračným súborom  predstavuje vstupnú bránu k simulácii, slúži na zmenu parametrov vykresľovania, zmenu hudobnej zložky a vstup do simulácie. Pre tvorbu grafických dát do menu som  využil pokročilé vlastnosti programu Photoshop CS3.
 +
 
 +
Užívateľské parametre zapísané do konfiguračného súboru vozidla sú základom pre vytvorenie vozidla s rôznymi proporciami. Vozidlo je ovládané priamou interakciou s užívateľom alebo algoritmom D* Lite. Pri priamej interakcii užívateľ prostredníctvom klávesnice naviguje vozidlo nejakým smerom. Pri nepriamej interakcii riadiaci algoritmus naviguje vozidlo k cieľu, určeného z modulu jazyka Python.
 +
 
 +
Asi najdôležitejšou časťou celej aplikácie je algoritmus zabezpečujúci interakciu medzi vozidlom a riadiacim algoritmom. Algoritmus prijíma vždy nový bod (budúcu polohu vozidla), vypočítaný riadiacim algoritmom. Následne rozpozná výhodnejší smer pohybu (vektor pohybu vzad / vpred).
 +
Ak je tento najvýhodnejší smer totožný so smerom do bodu, tak sa vykoná posun v danom smere (v závislosti na FPS), ak nie tak algoritmus musí vybrať najvýhodnejšiu operáciu (odčítať / pripočítať uhol), aby sa vozidlo natočilo na správny smer, a potom nastane posun. Ak sa dosiahne ponúknutý bod, vyžiadava sa vždy nový najvýhodnejší, až pokým vozidlo nedosiahne cieľ.
 +
 
 +
Zostavil som aj súbor algoritmov, ktoré dovoľujú užívateľovi definovať  parametre aproximačnej mapy na základe aproximačného polomeru. Riadiaci algoritmus D* Lite potom pracuje predovšetkým s takouto mapou, čo má za následok plynulejší prechod terénom a menšie nároky na procesor a pamäť.
 +
Nevyhnutnú súčasť simulačného prostredia predstavuje terén, ktorý je parametrizovaný priamo zo svojho konfiguračného súboru užívateľom alebo aplikáciou na základe parametrov pre algoritmus D* Lite. Užívateľ nastavuje napríklad počet šírkových a výškových podpriestorov (z ktorých vynásobením získame celkový počet podpriestorov), krok terénu (koľký bod v poradí bude načítavaný z výškovej mapy) a Chebyshevov polomer pre počet susedov (určuje maximálny možný počet susedov pre aproximáciu bodu mapy).
 +
 
 +
Vymyslel som algoritmus (súbor 4 algoritmov), ktorý sa snaží rovnomerne rozložiť body terénu do podpriestorov aj na základe kroku terénu. Plynulú výšku v teréne vytváram aproximáciou so susedmi bodu do vzdialenosti určenej užívateľom. Na dopočítanie výšok neexistujúcich bodov som definoval algoritmus, ktorý ich vyráta z roviny (trojuholníka existujúcich 3 bodov podľa kroku), v ktorom leží.   
 +
Výsledok práce v režime pohybu vozidla prezentujem pomocou piatich kamerových systémov (v režime bez vozidla je k dispozícii len 1), ktoré sú interaktívne a k dispozícii užívateľovi po celú dobu simulácie v režime s vozidlom.
 +
 
 +
Z programátorskeho hľadiska (pozri UML diagramy v prílohe D)  bola táto téma tvrdým orieškom z dôvodu obrovského rozsahu a náročnosti. Snažil som sa vytvoriť systém podobný stromovému grafu, kde vyššie postavený prvok vo vetve posiela „globálne” (globálne len v rámci tejto skupiny tried) zdieľané dáta nižšie postavenému členovi.
 +
 
 +
Na vrchole celej aplikácie sa nachádza trieda, ktorá jediná vie ako správne nastaviť a skonštruovať tieto dáta. Jediná má správny kľúč, ktorý použije ako parameter do šablóny triedy, ktorá je dedičom dátovej triedy (existuje špecializácia takejto šablóny so správnym kľúčom). Ak by sa použil hocijaký iný kľúč systém by skončil vyhodením výnimky (pre takýto prípad neexistuje špecializácia šablóny).
 +
 
 +
Posielanie dátovej triedy („globálne“ dáta) prebieha na základe pretypovania na rodiča (upcasting), aby sa neodhalil kľúč pre ostatné triedy v hierarchii. Vytvoril som triedu pre odchytávanie výnimiek aj triedu na logovanie, ktorá informuje užívateľa predovšetkým o chybách a upozorneniach systému. Niektoré kritické časti kódu som kvôli zvýšeniu rýchlosti preprogramoval pomocou metaprogramovania. To znamená, že výsledky sa tvoria už v čase kompilácie a aplikácia nie je zaťažovaná počas behu.
 +
 
 +
Veľký počet tried som zabezpečil tak, aby boli jednoinštančné, a to rekurzívnym dedením zo špeciálnej šablóny, ktorej parametrom je uvažovaná trieda.
 +
Rozvoj aplikácie môže prebiehať vo všetkých oblastiach. Ďalším krokom by mohlo byť napríklad vytvorenie multiagentového systému, pridanie možnosti tvoriť prekážky v teréne, aplikovanie fyzikálnych zákonov na vozidlo, zbavenie sa textových konfiguračných súborov a ich vloženie do systému menu, zrýchlenie aplikácie, zvýšenie parametrizácie kódu ďalšími šablónami, ošetrenie všetkých chybových situácií atď.
 +
 
 +
=Zoznam použitej literatúry=
 +
# ŽÁRA J. - BENEŠ B. - SOCHOR J. - FELKEL P. : Moderní počítačová grafika (2. vydání), Computer Press, 2005, ISBN 80-251-0454-0
 +
# WRIGHT R., Jr. - LIPCHAK B. - HAEMEL N. : OpenGL Superbible Fourth Edition, Addison-Wesley, 2007, ISBN 0-321-49882-8
 +
# ASTLE D. - HAWKINS K. : Beginning OpenGL Game Programming, Premier Press, 2004, ISBN 1-59200-369-9
 +
# SEDDON C. : OpenGL Game Development, Worldware Publishing, 2005, ISBN 1-55622-989-5
 +
# McREYNOLDS T. - B L Y T H E  D. : Advanced Graphics Programming using OpenGL, Morgan Kaufmann Publishers, 2005, ISBN 1-55860-659-9
 +
# MARTZ P.: OpenGL Distilled, Addison Wesley Proffesional, 2006, ISBN 0-321-33679-8
 +
# POLACK T. : Focus on 3d terrain programming, Premier Press, 2003, ISBN: 1-59200-028-2
 +
# OpenGL tutorial http://www.videotutorialsrock.com [1. 3. 2010]
 +
# The Official Guide to Learning OpenGL, Version 1.1. http://www.glprogramming.com/red/ [1. 3. 2010]
 +
# Seriál SDL: Hry nejen pro Linux http://www.root.cz/serialy/sdl-hry-nejen-pro-linux/ [1. 3. 2010]
 +
# View Frustum Culling Tutorial http://www.lighthouse3d.com/opengl/viewfrustum/ [1. 1. 2009]
 +
# A Library For Processing Structured Configuration Files, Version 1.4.4 http://www.hyperrealm.com/libconfig/libconfig_manual.html [1. 6. 2009]
 +
# Python (programovací jazyk) http://sk.wikipedia.org/wiki/Python_(programovací_jazyk) [1. 6. 2009]
 +
# Extending and Embedding the Python Interpreter http://docs.python.org/release/2.5.2/ext/ext.html [1. 4. 2010]
 +
# Chapter 1. python 1.0 http://www.boost.org/doc/libs/1_42_0/libs/python/doc/tutorial/doc/html/index [9. 10. 2009]
 +
# Path Planning with D*Lite http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.67.6521 [1. 6. 2009]
 +
# FPS: Konstantní rychlost animace http://nehe.ceske-hry.cz/cl_fps.php [6. 6. 2009]

Aktuálna revízia z 22:50, 30. august 2010

Obsah práce
1. Teoretické poznatky a metódy
2. Multi-analýza a syntéza simulačného programu

Interakcia s užívateľom

  1. MENU
    • (a) Ľavé tlačidlo myši + pohyb myši (výber z ponuky, nastavovanie)
    • (b) Klávesa ESC (ukončenie práce s programom - menu)
  2. SIMULAČNÉ PROSTREDIE
    • Klávesa ESC (ukončenie práce v sim. prostredí, návrat do menu)
    • Klávesa F6 (začiatok simulácie vozidla)
    • Klávesa F10 (priama interakcia s vozidlom / UI )
  3. VOZIDLO-PRIAMA INTERAKCIA
    • Klávesa L (odpočet k uhlu kolies [-])
    • Klávesa J (prípočet k uhlu kolies [+])
    • Klávesa V (prípočet k veľkosti rýchlosti)
    • Klávesa C (zmenšenie veľkosti rýchlosti)
    • Klávesa I (pohyb vpred určenou rýchlosťou)
    • Klávesa K (pohyb vzad určenou rýchlosťou)
  4. KAMEROVÉ SYSTÉMY
    • Klávesa F2 (kamera 'Lietanie')
    • Klávesa F3 (kamera 'Prezentačná', len v režime s vozidlom)
    • Klávesa F4 (kamera 'Za vozidlom', len v režime s vozidlom)
    • Klávesa F5 (kamera 'Rotačná', len v režime s vozidlom)
  5. KAMERA – LIETANIE
    • Klávesa W (posun kamery v smere vektora pozorovania)
    • Klávesa S (posun kamery v protismere vektora pozorovania)
    • Klávesa A (posun kamery v protismere vektora vpravo)
    • Klávesa D (posun kamery v smere vektora vpravo)
    • Klávesa R (zväčšenie rýchlosti posunu)
    • Klávesa E (zmenšenie rýchlosti posunu)

Menu

Konfiguračný súbor a parser konštruujúci menu

Základom pre vytvorenie menu podľa užívateľských požiadaviek je môj vlastný typ konfiguračného súboru. Pri zápise do konfiguračného súboru treba dbať na dodržiavanie niektorých pravidiel, ktorými sa riadi parser konštruujúci menu.

Obr. 18 Ukážka sekcie 'obrazky' konf. súboru konšt. menu
  1. Pravidlá vyplývajúce z algoritmu parsera na úpravu tohto textu
    1. komentáre začínajú vždy znakom *
    2. ak má byť posledný údaj na riadku (najviac vpravo) textový reťazec, tak jeho posledný znak je prvý znak sprava po odstránení nežiaducich znakov ("\t \n\r") algoritmom parsera, čiže nepočítajme so zahrnutím týchto znakov ku koncu posledného reťazca v riadku
  2. Pravidlá vyplývajúce zo spôsobu spracovania údajov
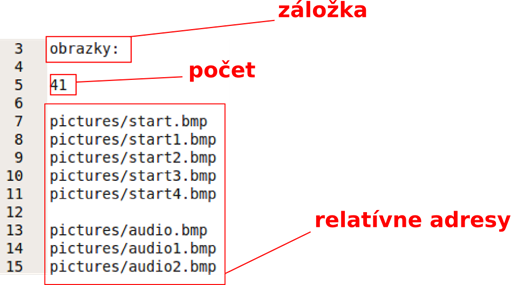
    1. súbor je logicky rozdelený do 2 sekcií, ktorých začiatky musia byť vyznačené záložkami 'obrazky:' alebo 'pic_stranky:' podľa obsahu pod ním ; každá sekcia sa môže nachádzať na ľubovoľnom mieste v súbore
    2. sekcia 'obrázky:' vždy začína (v danom poradí):
      • počtom obrázkov
      • jednotlivými adresami obrázkov daného počtu (poradie v akom sú adresy obrázkov zapísané určí im ich index, ktorý bude používaný v sekcii pic_stranky:')
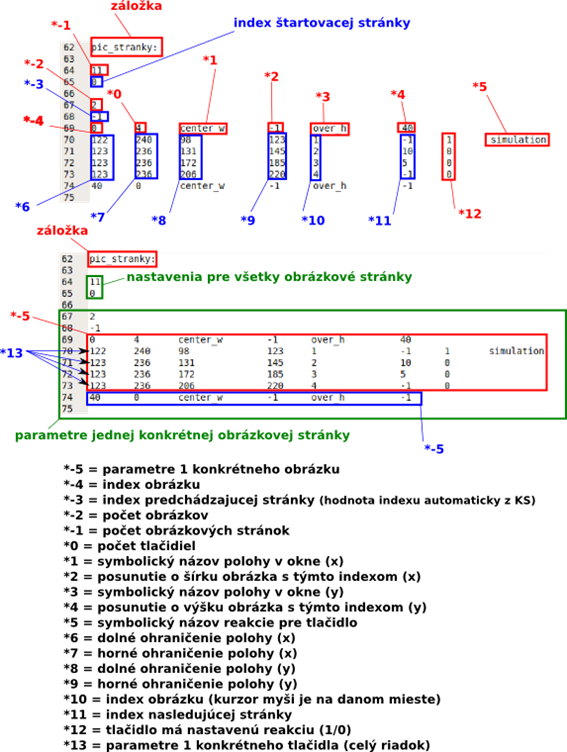
    3. sekcia 'pic_stranky:' musí začínať vždy (v danom poradí):
      • počtom obrázkových stránok
      • indexom štartovacej stránky
      • Nasledujúci súbor pravidiel sa opakuje podľa počtu obrázkových stránok:
        • počet obrázkov v obrázkovej stránke
        • index predchádzajúcej stránky (z ktorej sme sa sem dostali), ak je -1, tak neexistuje predchádzajúcu stránka (prvá spustená stránka nemá predchádzajúcu)
        • Nasledujúci súbor pravidiel sa opakuje podľa počtu obrázkov v stránke:
            • index obrázka (určený poradím adries v sekcii 'obrazky:')
            • počet oblastí v aktuálnom obrázku, ktoré budú používané ako tlačidlá
            • jeden zo symbolických názvov (left_w, center_w, rigth_w) , ktorý určí prvotnú polohu v okne vzhľadom na šírku okna
            • index obrázka, ktorý určí prípočet k prvotnej polohe vzhľadom na šírku (používa sa na relatívnu orientáciu vzhľadom na iný obrázok, ak je -1 tak neexistuje)
            • jeden zo symbolických názvov (bottom_h, center_h, over_h) , ktorý určí prvotnú polohu v okne vzhľadom na výšku okna
            • index obrázka, ktorý určí prípočet k prvotnej polohe vzhľadom na výšku (používa sa na relatívnu orientáciu vzhľadom na iný obrázok, ak je -1 tak neexistuje)
            • Nasledujúci súbor pravidiel sa opakuje podľa počtu tlačidiel v stránke (pzn.: počiatok súradnicového systému tlačidla je v ľavom hornom rohu obrázku, v ktorom sa nachádza):
              • súradnica ohraničujúca oblasť tlačidla zľava (os x)
              • súradnica ohraničujúca oblasť tlačidla zprava (os x)
              • súradnica ohraničujúca oblasť tlačidla zhora (os y)
              • súradnica ohraničujúca oblasť tlačidla zdola (os y)
              • index obrázku, ktorý sa vykreslí po vstúpení na oblasť (kurzorom myši) ohraničenú daným tlačidlom v danom obrázku a v danej obr. Stránke
              • index nasledujúcej stránky, na ktorú sa užívateľ dostane po kliknutí na toto tlačidlo(ak neexistuje označíme -1, index sa automaticky priradzuje podľa poradia obr. stránky v konfig. súbore)
              • boolovske ohodnotenie, či dané tlačidlo využíva nejakú reakciu (0/1)
              • ak predchádzajúci bod bol označený ako 1, treba vybrať 1 zo symbolických názvov, ktoré väčšinou samoopisujú svoje využitie (simulation, bpp_to_32bit, bpp_to_16bit, resolution_to_1024x768, resolution_to_800x600, resolution_to_640x480, volume_music_down, volume_music_up, volume_sound_down, volume_sound_up, play_song_united, play_song_breaking, play_song_war, play_song_black, gamma_down , gamma_up, to_fullscreen)
Obr. 19 Časť zo sekcie 'pic_stranky' konfiguračného súboru konštruujúceho menu

Všeobecný opis a využitie

Obr. 20 Konfiguračný súbor parametrov vykresľovania

Menu je flexibilné vďaka konštrukčnému konfiguračnému súboru, ktorý si užívateľ prepíše podľa svojich potrieb, ale podľa pravidiel opísaných v predchádzajúcej časti (pravidlá pre parser). Menu pozostáva z menších logických úsekov, ktoré označujeme ako obrázkové stránky. Každej stránke môžeme prideliť ľubovoľný počet obrázkov a index predchádzajúcej stránky (štartovacia stránka nemá ukazovateľ na predchádzajúcu stránku). Obrázok každej stránky má množstvo parametrov. Môžeme meniť polohu každého obrázka vzhľadom na polohu v okne a súčasne aj orientovať jeho polohu voči ostatným obrázkom v stránke.

Významnou vlastnosťou je, že každý obrázok môže pozostávať ešte z menších úsekov, tlačidiel, ktoré ešte viac rozširujú schopnosti menu. Tlačidlu môžeme priradiť určitý druh reakcie a index nasledujúcej stránky alebo len index na nasledujúcu stránku. Pod pojmom reakcia môžeme chápať napríklad zmenu rozlíšenia (užívateľ vyberá reakciu zadaním symbolického názvu). Index na nasledujúcu stránku zaznamenáva jedinečné číslo stránky, ktorá sa vykreslí po stlačení tlačidla (posun na ďalšiu úroveň).

Ďalej môžeme nastaviť, v ktorej časti obrázku sa bude tlačidlo nachádzať, zadaním 4 hodnôt (2 pre os X, 2 pre os Y), ktoré vytvoria ohraničenie. Na ukladanie informácií o rozlíšení, bitovej hĺbke (parametre vykresľovania) a ďalších používam konfiguračný súbor z knižnice Libconfig (Obrázok 20). Pri novom štarte programu sa tieto uložené informácie automaticky použijú ako prvotné nastavenia premenných. Prvotné nastavenie pre jednotlivé parametre je použité pri prvom spustení programu (Obrázok 20: premenná 'screen_first_time'), napríklad rozlíšenie by bolo 640x480.

Flexibilita menu sa prejavuje aj jednoduchosťou rozšírenia množiny reakcií alebo polôh v okne priamo v zdrojovom kóde. Programátor by len jednoducho vytvoril ďalšiu metódu a pridal adresu metódy do poľa prislúchajúceho množine adries reakcií/polôh a symbolický názov do množiny symbolických názvov reakcií/polôh. Následne môže použiť symbolický názov v konfiguračnom súbore. Grafický systém menu bol vytvorený vo Photoshop CS3 použitím rôznych pokročilých geometrických a filtračných metód.

Vozidlo

Vytvorenie vozidla

Obr. 21 Konfiguračný súbor vozidla

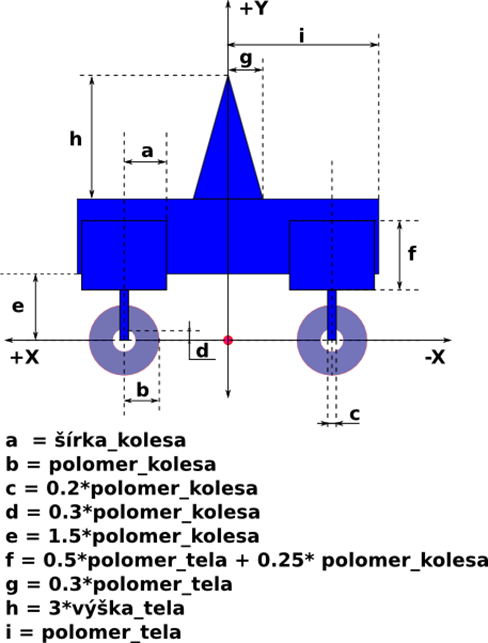
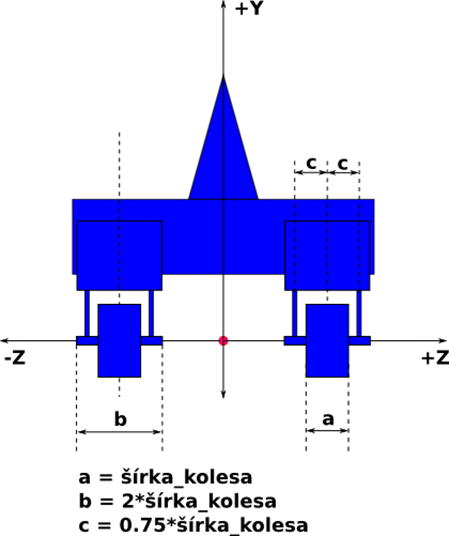
Jednotlivé časti vozidla sa vytvárajú (alebo sú na nich závislé) podľa užívateľom zapísaných hodnôt do konfiguračného súboru (Obrázok 21). Parametre, ktoré si užívateľ určuje:

  1. polomer tela vozidla
  2. výšku tela vozidla
  3. polomer kolesa
  4. šírka kolesa
Obr. 22 Vozidlo (XY)

Koštrukcia vozidla sa delí na dve časti, vytvorenie tela vozidla a podvozku. Telo vozidla pozostáva:

  1. Valec uzatvorený na oboch koncoch dvoma diskami
  2. Kužeľ

Tvorba podvozku je omnoho zložitejšia, pretože musí zohľadniť množstvo vzájomných zavislostí. Podvozok pozostáva :

  1. 4 valce uzatvorené čiastočne na oboch koncoch diskami (kolesá vozidla, čiastočne uzatvorené, pretože každé koleso potrebujeme spojiť s telom)
  2. 4 horizontálne valce úplne uzatvorené dvoma diskami (prechádzajú kolesami)
  3. 8 úzkych vertikálnych valcov úplne uzatvorených dvoma diskami (vytvárajú spojenie medzi horizontálnym valcom a širokým vertikálnym valcom )
  4. 4 široké vertikálne valce úplne uzatvorené dvoma diskami (vytvárajú spojenie medzi telom vozidla a 2 úzkymi valcami každého kolesa
Obr. 23 Vozidlo (XZ)

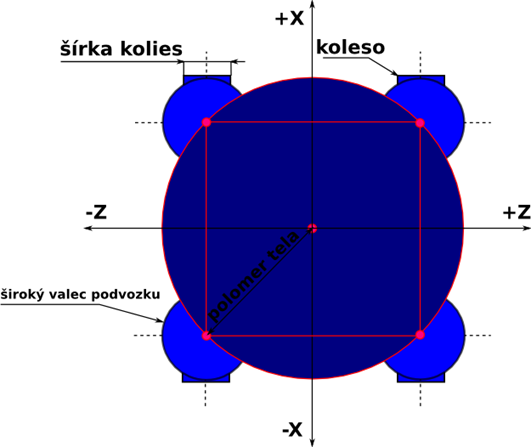
Polohy kolies (na osiach X, Z) musia byť vyjadrené relatívne k polohe aktuálneho ťažiska (poloha na Y sa neurčuje, vyplynie z rotácie (uhly na základe polohy kolies v teréne) vozidla okolo ťažiska – rotácia okolo X, Z ). Pre určenie polôh kolies (X,Z) využívam známy vzťah kružnice opísanej štvorcu. Strana štvorca, ktorému je opísaná kružnica (telo vozidla):

[math]a=\sqrt{2}*polomer\_tela[/math]

Pre polohy kolies v súradnicovom systéme vozidla (X, Z) potom platí:

[math]\begin{matrix} \check{l}av\acute{e}\_zadn\acute{e}=[-a/2,-a/2] \\ prav\acute{e}\_zadn\acute{e}=[-a/2,+a/2] \\ \check{l}av\acute{e}\_predn\acute{e}=[+a/2,-a/2] \\ prav\acute{e}\_predn\acute{e}=[+a/2,+a/2] \\ \end{matrix}[/math]

Obr. 24 Vozidlo (YZ)

Pohyb vozidla v teréne

Vozidlo môže byť riadené priamo užívateľom k ľubovoľnému cieľu alebo riadiacim algoritmom k určenému cieľu v teréne (cieľ určuje riadiaca trieda z jazyka Python). Tieto režimy majú spoločné tri algoritmy, ktoré majú za úlohu správnu interakciu s terénom a vykreslenie v teréne.

Prvý z nich (Pseudoalgoritmus 1) výpočíta nové ťažisko na osiach X, Z v súradnicovom systéme terénu a nový uhol natočenia kolies okolo vlastnej osi Z (algoritmus potrebuje poznať správny smer pohybu vozidla, jeho veľkosť aj FPS).


Pseudoalgoritmus 1

Druhý (Pseudoalgoritmus 11, pozri prílohu B) je omnoho komplikovanejší a preberá informácie z prvého. Počíta dotykové body kolies s terénom na osiach X, Y, Z, počíta súradnicu Y ťažiska, uhly natočenia vozidla okolo tohto ťažiska (rotácia okolo X, Z na základe polôh kolies v teréne), bod vrcholu kužeľa kontroluje správnosť výpočtu (či može existovať vozidlo v teréne na danej polohe).

Tento algoritmus (Pseudoalgoritmus 11) využíva aj algoritmus na výpočet výšky v teréne pre ľubovoľné aj desatinné hodnoty súradníc (Pseudoalgoritmus 10, príloha B). Pre desatinné súradnice X, Z je výška zistená z roviny (trojuholníka), v ktorej leží v teréne. Tieto 2 algoritmy sa vykonávajú len v prípade pohybu alebo pri prvej konštrukcii vozidla v teréne. Tretí algoritmus vykresľuje vozidlo na vypočítanom mieste v teréne s určenými uhlami (Pseudoalgoritmus 15, príloha B).

Vozidlo ovládané užívateľom

Komunikácia s vozidlom prostredníctvom klávesnice:

  1. Žiadaná akcia: Rotácia kolies (360°). Reakcia v danom poradí:
    1. Natočenie kolies o žiadaný uhol
    2. Pseudoalgoritmus 15
  2. Žiadaná akcia: Pohyb vpred/vzad určenou rýchlosťou. Reakcia v danom poradí:
    1. Záloha
    2. Pseudoalgoritmus 1
    3. Pseudoalgoritmus 11 => Úspech / Neúspech => Obnova
    4. Pseudoalgoritmus 15
  3. Žiadaná akcia: Zmenšenie/zväčšenie veľkosti rýchlosti. Reakcia v danom poradí:
    1. Vykoná/Nevykoná sa
    2. Pseudoalgoritmus 15

Všetky detaily toku programu v tomto režime sú jasne zobrazené ako Vývojový_diagram 1, v prílohe C. Pseudoalgoritmus 11/15 nájdete v prílohe B.

Simulácia pohybu vozidla ovládaného UI k cieľu

Tok programu v tomto režime nájdete v prílohe C ako Vývojový_diagram 2.

  1. Úloha : Nájsť cestu z bodu A do bodu B – správne navigovať vozidlo bez priameho zásahu užívateľa.
  2. Predpoklady
    1. Terén, diskrétny 8-smerový priestor.
      1. bod terénu
        • priechodný - vyznačuje sa cenou cesty do cieľa, cenou cesty do cieľa cez najlepšieho suseda, vlastnou cenou >= 0 (výškou)
        • nepriechodný – prekážka, vyznačuje sa cenou cesty do cieľa = [math]\infty [/math], cenou cesty do cieľa cez najlepšieho suseda = [math]\infty [/math], vlastnou cenou < 0
          • prekážky vyplývajúce z ohraničenia terénu vzhľadom na vozidlo
          • prekážky vyplývajúce z max. rozdielu dvoch po sebe idúcich výšok ↔ vlastných cien (určované užívateľom)
      2. možnosť aproximovať body terénu podľa zvoleného polomeru (určované užívateľom) → prirodzenejší pohyb vozidla smerom k cieľu, ale aj zvačšená nepresnosť
    2. Vozidlo
      1. informácie o prostredí sú často nekompletné → riešenie využívajúce len počiatočné informácie môže byť nesprávne alebo neoptimálne
      2. aktualizácia informácií v každej novej pozícii vozidla na základe senzoru a iných prostriedkov (polomer senzoru určovaný užívateľom)
      3. preplánovanie cesty na základe nových podmienok (zmení sa cena dôležitého bodu)
  3. Riešenie: Algoritmus D * Lite (finálna vezia), pravidelne zisťuje najkratšie cesty medzi súčasnou pozíciou vozidla a cieľovou pozíciou ako ceny prechodov v teréne, ktoré sa menia počas toho ako sa robot presúva smerom k cieľu

Užívateľ nastavuje tri parametre potrebné pre správne fungovanie mojej implementácie riadiaceho algoritmu D * Lite (konečná verzia):

  1. polomer dosahu senzoru vozidla (Chebyshevova vzdialenosť)
  2. polomer aproximácie bodu výškovej mapy (Chebyshevova vzdialenosť)
  3. maximálny rozdiel výšok (súradnica Y) dvoch po sebe nasledujúcich bodov terénu (susedov)
Obr. 25 Konfiguračný súbor riadiaceho algoritmu

Výpočet heuristickej vzdialenosti medzi bodmi na základe Chebyshevovej vzdialenosti:

Pseudoalgoritmus 2

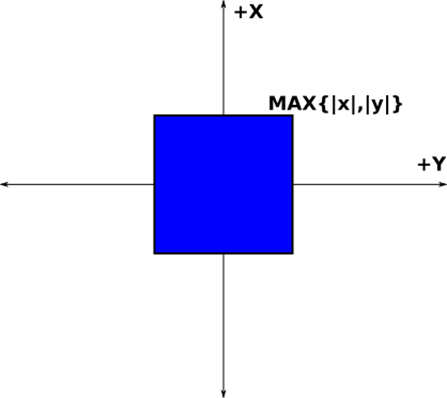
Chebyshevova vzdialenosť alebo vzdialenosť na základe maximálnej hodnoty sa často používa ako odhad euklidovskej vzdialenosti kvôli menšej časovej náročnosti výpočtu. Táto vzdialenosť je jednoducho maximum z rozdielov súradníc. S takouto funkciou výpočtu vzdialenosti je kruh v [math]R^2[/math] štvorec a guľa v [math]R^3[/math] je kocka.

Pre túto vzdialenosť medzi vektormi alebo bodmi p a q so štandardnými súradnicami [math]p_i a q_i[/math] platí :

[math]{{D}_{Chebyshev}}(p,q):=\underset{i}{\mathop{max}}\,({{p}_{i}}-{{q}_{i}})[/math],

zároveň sa rovná limite vzdialenosti v sústave

[math]{{L}_{p}}:\underset{k\to \infty }{\mathop{\text{lim}}}\,{{(\underset{i=1}{\overset{p}{\mathop \sum }}\,{{p}_{i}}-{{q}_{i}}^{p})}^{\frac{1}{p}}}[/math].

Obr. 26 Chebyshevova vzdialenosť (2D)


Výpočet ceny prechodu medzi stavmi

Cena prechodu z jedného bodu na druhý (priechodné body) sa počíta na základe klesania/ stúpania alebo rovnej cesty, pričom klesanie je považované za najvýhodnejšie. Čím je výraznejšie stúpanie tým aj cena cesty je väčšia a pod.

Pseudoalgoritmus 3


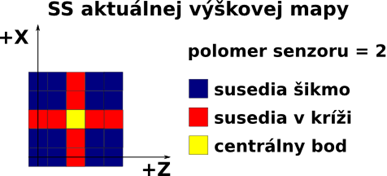
Výpočet množiny susedov bodu na určenej pozícii na základe Chebyshevovej vzdialenosti – informácie zo senzoru

Zahŕňa všetky možné body aj prekážky, ktoré spĺňajú vzdialenosť od centrálneho bodu a ohraničenie terénu (používaná mapa = pôvodná/aproximačná). Algoritmus (Pseudoalgoritmus 12 v prílohe B, obrázok 27) na zistenie kompletnej množiny prebieha v 2 fázach: Nájdenie všetkých možných susedov v kríži do danej vzdialenosti (1 súradnica nulová) a nájdenie všetkých susedov šikmo (nenulové súradnice X, Z).

Existencia suseda šikmo sa vždy určuje na základe kombinácie existencie obidvoch súradníc X, Z, čiže na základe existencie horizontálneho a vertikálneho suseda v kríži na uvažovaných súradniciach. Napríklad sused [3,3] je sused šikmo a existuje len ak existujú susedia v kríži [0,3] a [3,0]. Maximálny počet takýchto susedov som vypočítal ako [math]4*(vzdialenost+vzdialenos{{t}^{2}})[/math].

Obr. 27 Chebyshevov senzor vozidla

Výpočet a úprava hodnôt potrebných pre aproximáciu výškovej mapy

Ak má nastať aproximácia pôvodnej výškovej mapy, musí užívateľ zvoliť aproximačný polomer >0, následne sa odvodzujú a upravujú ďalšie potrebné hodnoty. Môže nastať aj zmenšenie šírky/výšky v teréne (ak nevyhovuje) tak, aby šírka/výška terénu bola násobkom strany aproximačného štvorca.

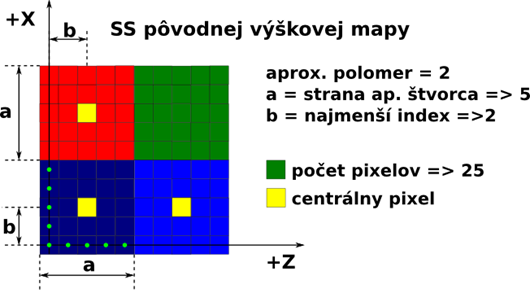
Stranu aproximačného štvorca som odvodil veľmi jednoducho. Zahrnieme do nej 1 centrálny bod a jeho 2 krídla, ktoré som odvodil ako 2*aprox_polomer. Najmenší index (prvá možná súradnica stredu aprox. štvorca) v pôvodnej mape som určil ako aprox"_" polomer(Ukážka aproximačných štvorcov pre polomer 2 je na obrázku 28).


[math]\begin{align} & \text{strana}\_\text{aprox}\_s\text{tvorca}\leftarrow 1+2\text{*aprox}\_\text{polomer} \\ & \text{najmensi}\_\text{index}\_\text{stredu}\_\text{aprox}\_s\text{tvorca}\leftarrow \text{aprox}\_\text{polomer} \\ & \\ & \text{pocet}\_\text{pixelov}\_\text{v}\_\text{aprox}\_s\text{tvorci}\leftarrow 4\text{*}(\text{aprox}\_\text{polomer}+\text{aprox}\_\text{polome}{{\text{r}}^{2}})+1 \\ & \text{sirk}{{\text{a}}_{\text{terenu}}}\leftarrow si\text{rk}{{\text{a}}_{\text{terenu}}}-(si\text{rk}{{\text{a}}_{\text{terenu}}}%\text{strana}\_\text{aprox}\_s\text{tvorca}) \\ & \text{vysk}{{\text{a}}_{\text{terenu}}}\leftarrow \text{vysk}{{\text{a}}_{\text{terenu}}}-(\text{vysk}{{\text{a}}_{\text{terenu}}}%\text{strana}\_\text{aprox}\_s\text{tvorca}) \\ & \\ & \text{sirk}{{\text{a}}_{\text{aprox}\_\text{mapy}}}\leftarrow \text{sirk}{{\text{a}}_{\text{terenu}}}/\text{strana}\_\text{aprox}\_\text{stvorca} \\ & \text{vysk}{{\text{a}}_{\text{aprox}\_\text{mapy}}}\leftarrow \text{vysk}{{\text{a}}_{\text{terenu}}}/\text{strana}\_\text{aprox}\_\text{stvorca} \\ \end{align}[/math]

Obr.28 Aproximačné štvorce


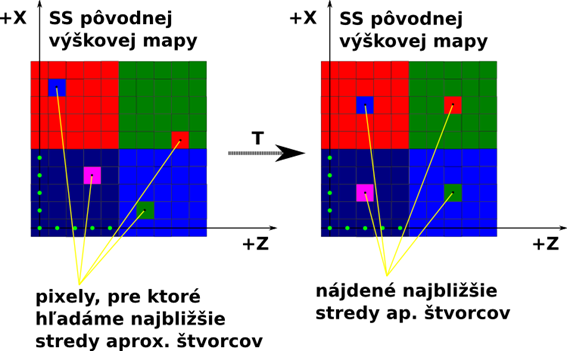
Nájdenie najbližšieho stredu aproximačného Chebyshevovho štvorca

Tento výpočet je potrebný ako prvý krok pre celkovú transformáciu do aproximačnej mapy. Každému bodu pôvodnej mapy (X, Z) môžeme priradiť pre neho najbližší centrálny bod aproximačného štvorca (Pseudoalgoritmus 4, obrázok 29).


Pseudoalgoritmus 4
Obr. 29 Nájdenie najbližšieho stredu aprox. štvorca

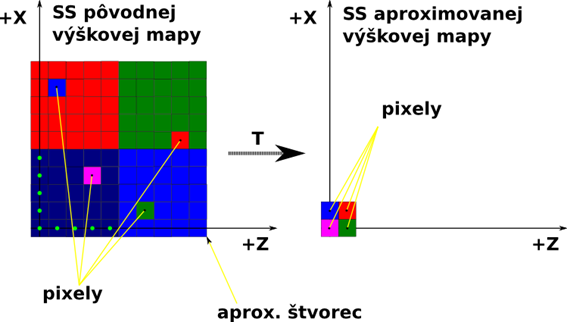
Transformácia z normálneho priestoru (pôvodná výšková mapa) do aproximačného priestoru (aproximačná výšková mapa), (Pseudoalgoritmus 5, Obrázok 30)

Pseudoalgoritmus 5
Obr. 30 Transformácia do aproximovaného priestoru


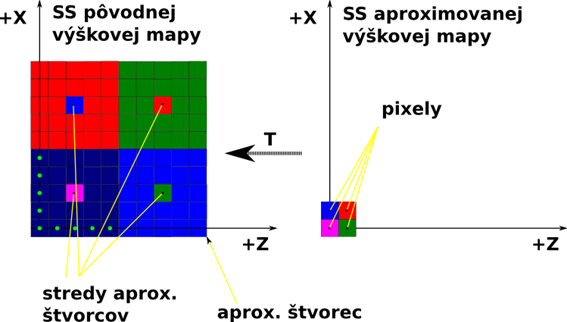
Transformácia z aproximačného priestoru (aproximačná výšková mapa) do normálneho priestoru (pôvodná výšková mapa)

Pseudoalgoritmus 6

Jednou veľkou nevýhodou takejto transformácie (Pseudoalgoritmus 6, obrázok 31), že transformované body sa budú len s určitou presnosťou približovať pôvodnej hodnote (ak neboli stredmi aproximačných štvorcov) , pretože sú „orezané“ ako stredy aprox. štvorcov. Ak by to tak nemalo byť, musel by sa zmeniť celý systém aproximácie, aby táto transformácia ponúkala reálnu hodnotu, z ktorej bola predtým vypočítaná.

Obr. 31 Transformácia do pôvodného priestoru


Výpočet výšky pre jeden aproximačný štvorec normálneho priestoru

Tento algoritmus (Pseudoalgoritmus 7) je triviálny, pretože v podstate vypočíta všetkých možných susedov do určenej vzdialenosti (aprox. polomer) vzhľadom na určený centrálny bod (Pseudoalgoritmus 12, príloha B). Následne vypočíta priemer výšky (1 bod aproximačného priestoru) vzhľadom na tento počet susedov + 1 (stred).

Pseudoalgoritmus 7


Vytvorenie aproximačnej výškovej mapy

Dáta aproximačnej mapy sa vytvoria tak (Pseudoalgoritmus 8), že sa prechádza celá pôvodná mapa v šírke/výške od najmenšej možnej súradnice aprox. štvorca, pričom inkrementácia pre šírku/výšku je zväčšenie o veľkosť strany aprox. štvorca. V každom takomto úseku sa vypočíta aproximácia pre celý 1 aproximačný štvorec (nemusí byť štvorec ak niektoré body sú mimo terénu – nebudú zahrnuté do výpočtu) pôvodnej mapy (Pseudoalgoritmus 7) a uloží sa ako hodnota do aproximačnej mapy.

Počiatočný index v šírke/výške pôvodnej mapy je aprox_polomer (pozri : 'Výpočet a úprava hodnôt potrebných pre aproximáciu výškovej mapy').

Pseudoalgoritmus 8


Posun vozidla na aktuálnu polohu ↔ najlepšieho nasledovníka predchádzajúcej polohy (Pseudoalgoritmus 13, príloha B)

Stavy, ktoré budú posudzované vzhľadom na aktuálnu situáciu (polohu vozidla), pričom práca prebieha v aktuálnom priestore ↔ pôvodný / aproximačný:

  1. informácie zo senzoru
  2. možná skupina bodov z minulej polohy vozidla, ktorí boli označení ako lokálne prekážky musia byť prehodnotení vzhľadom na aktuálnu polohu

Posudzovanie zistených stavov:

  1. posudzovanie len v pôvodnom priestore
    1. Ak je priechodný ∧nie je už známy ako prekážka ∧spĺňa podmienku globálnej prekážky → globálna prekážka – platná stále (bezpečná zóna pre vozidlo vo forme nevizuálnych prekážok pri hraniciach diskrétneho terénu)
  2. posudzovanie vo vlastnom priestore – pôvodný / aproximačný
    1. Ak je najbližší priechodný (heuristika = 1)∧nie je už známy ako globálna prekážka ∧nespĺňa podmienku maximálneho rozdielu výšok → lokálna prekážka
    2. (Ak je priechodný∧nie je už známy ako prekážka) ∧(je úplne nový ∨rozdielny voči pôvodnej hodnote) → priechodný bod


Interakcia medzi vozidlom a vysokoúrovňovým riadiacim algoritmom (Pseudoalgoritmus 14, príloha B)

Zjednodušený opis, v danom poradí bodov činnosti :

  1. Výpočet celočíselneho štartovacieho bodu z aktuálnej polohy vozidla, v závislosti od možnosti zvoliť si aproximáciu výškovej mapy, čiže vypočítaná poloha bude jednoduchým zaokrúhlením (bez aproximácie) na najbližšie celé číslo alebo stredom aproximačného štvorca (aproximácia) s rozlišovaním prekážok
  2. Vozidlo príjme informácie o nasledujúcej polohe bodu z D* Lite, musí podniknúť také kroky, aby ho dosiahol
    1. (Ak smer pohybu vozidla ∨opačný vektor k smeru vozidla – smer vzad) ∧smer k ponúknutému bodu (všetky tri sú jednotkové vektory charakteristické len smerom a dvojdimenzionálne- X, Z, počiatok majú v aktuálnej polohe ťažiska ) sú totožné, čiže uhol medzi 1 z vektorov pohybu vpred alebo vzad a vektorom smeru k bodu je 0, môže nastať posun v tomto smere k ponúknutému bodu (dopredu/dozadu) → pokračuje sa bodom B.III, inak pokračuj na B.II
    2. (Ak smer pohybu vozidla ∨opačný vektor k smeru vozidla) ∧vektor smeru k ponúknutému bodu nie sú totožné, čiže uhol medzi vektorom pohybu vpred/vzad a vektorom smeru k bodu nie je 0, nemôže nastať posun v tomto smere k ponúknutému bodu (dopredu/dozadu). Musí sa zabezpečiť natočenie kolies vozidla do správneho uhla tak, aby jeden z vektorov pohybu (výhodnejší z vpred/vzad na natočenie pre hľadaný smer) bol totožný s vektorom do budúcej polohy vozidla, k ideálnejšiemu vektoru pohybu sa pripočíta/odčíta malá koštanta (podľa FPS) tak, aby sa priblížil k hľadanému smeru, pokračujeme bodom B.I.
    3. Nastáva pohyb v správnom smere k bodu (vektor pohybu vpred alebo vzad je totožný so smerom k tomuto bodu), posunieme sa o malý kúsok (pripočíta/odčíta)
    4. Ak sme dosiahli požadovaný bod a nebol to cieľ tak D* Lite vypočíta a pošle nasledujúci najlepší bod v závislosti na rôznych parametroch, ak dosiahnutý bod je cieľ tak práca končí, ináč sa pokračuje bodom B.I.

Vykresľovanie vozidla

Jednotlivé časti vozidla sú hierarchicky usporiadané a uložené vo forme display listov. Počet všetkých častí je 22. Ich poloha je relatívne vyjadrená voči aktuálnej polohe ťažiska v teréne. Každá konštrukčná jednotka prislúcha podvozku alebo telu vozidla. Vyjadrenie správneho umiestnenia prebieha na základe maticového násobenia.

Obr. 32 Vozidlo v teréne


Terén

Vytvorenie terénu

Konštrukcia terénu je ovplyvnená mnohými požiadavkami, ktoré užívateľ zapisuje do konfiguračného súboru:

  1. rozmery terénu – väčšinou ich užívateľ volí totožne s rozmermi výškovej mapy [môžu byť upravené v závislosti na polomere aproximácie pre D* Lite]
    1. výška
    2. šírka
  2. počet podpriestorov – terén bude logicky rozdelený do podpriestorov (počet= počet šírkových * počet výškových), vo forme kvádru (8 bodov) a budú slúžiť na efektivizáciu vykresľovania terénu
    1. počet šírkových podpriestorov
    2. počet výškových podpriestorov
  3. krok terénu – určuje koľký bod v poradí bude načítavaný pri prechádzaní šírkou a výškou mapy
  4. počet susedov – Chebyshevov polomer, ktorý rozhoduje o množstve susedov pre aproximovanie každého pixelu ako centrálneho bodu
Obr. 33 Konfiguračný súbor terénu

Výšková mapa predstavuje obrázok v stupňoch 1 farby (1 byte na pixel), t.j. každý jeden pixel obrázku môže nadobúdať hodnotu od 0 do 255. Táto hodnota predstavuje vstupnú (bude sa pravdepodobne meniť) výšku bodu v teréne.

Postupnosť vykonania algoritmov pre správne vytvorenie terénu:

  1. Vytvorenie správnych hraníc podpriestorov
    1. Zistenie hraníc šírkových podpriestorov
    2. Zistenie hraníc výškových podpriestorov
    3. Upravenie rozdelených hraníc šírkových podpriestorov podľa kroku terénu
    4. Upravenie rozdelených hraníc výškových podpriestorov podľa kroku terénu
  2. Hlavný cyklus
    1. Konštrukcia bodov terénu v závislosti od množstva parametrov
  3. Vytvorenie plynulej výšky v teréne
  4. Výpočet správnych normálových vektorov pre každý bod vzhľadom na susedov
  5. Dopočítanie výšok neexistujúcich celočíselných bodov terénu


Zistenie hraníc šírkových podpriestorov

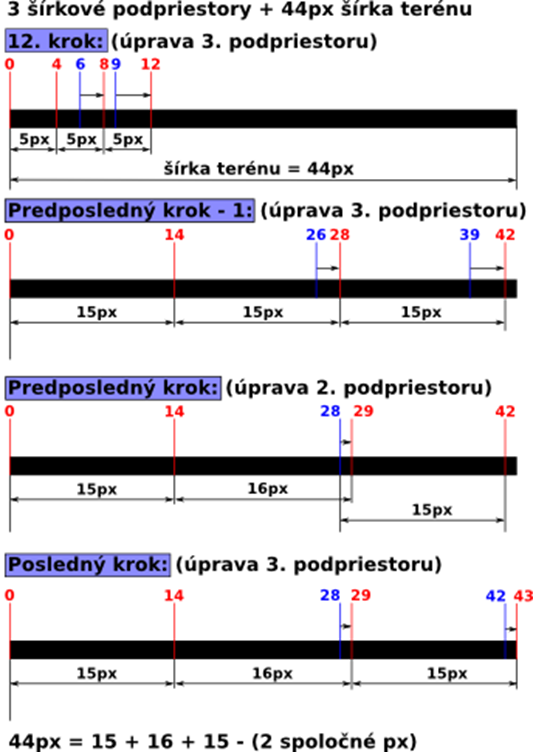
Podpriestory rozdeľujú priestor do menších blokov. Tvorba šírkových podpriestorov (Pseudoalgoritmus 16 v prílohe B, obrázok 34) je prvým krokom k vytvoreniu podpriestorov, ktoré obsahujú rovnaký počet bodov vzhľadom aj na krok terénu. Algoritmus postupne rovnomerne prideľuje súradnice do jednotlivých šírkových podpriestorov, čiže posúva ich hranice. Horná hranica posledného ŠP sa po skončení výpočtov musí rovnať poslednej súradnici šírky terénu a zároveň dolná hranica prvého ŠP musí byť 0. Algoritmus zväčšuje veľkosti všetkých podpriestorov len ak má istotu, že má dostatočný počet iterácií vzhľadom na počet ŠP. Môže nastať situácia, že počet zostávajúcich iterácií (počet súradníc ktoré treba prerozdeliť) je menší ako celkový počet ŠP. V takomto prípade algoritmus určí, od ktorého ŠP má začať prerozdeľovať tak, aby sa dostal až k poslednému ŠP.

Obr. 34 Ukážka algoritmu (ZHŠP) na konkrétnych hodnotách


Upravenie rovnomerne rozdelených hraníc šírkových podpriestorov podľa kroku terénu

Tento algoritmus (Pseudoalgoritmus 9) sa aplikuje až po rovnomernom rozdelení do šírkových podpriestorov (Pseudoalgoritmus 16, príloha B).

Cyklus tohto algoritmu je vlastne prechádzanie šírky terénu po krokoch terénu. Kontroluje, či niektorý zo šírkových podpriestorov nemá svoju hornú hranicu menšiu ako je aktuálny index (násobok kroku terénu) v cykle. Ak táto podmienka platí tak musí nastať posunutie tejto hornej hranice na dobrú hodnotu (z predchádzajúceho cyklu) a zároveň v dôsledku nunosti naväzovania ŠP musí byť rovnako nastavená aj dolná hranica nasledujúceho ŠP.


Pseudoalgoritmus 9


Dopočítanie neexistujúcich výšok bodov terénu

Užívateľ v konfiguračnom súbore nastavuje veľkosť kroku terénu, ktorým sa dá jednoducho regulovať plynulosť terénu a zároveň aj pamäťové nároky. Lenže s aplikáciou kroku terénu >1vzniká potreba dopočítať ostatné neznáme výšky (ak [math](bo{{d}_{x}}%krok)\ne 0\vee (bo{{d}_{z}}%krok)\ne 0[/math] ), ktoré boli automaticky vylúčené z výškovej mapy (dopočítanie potrebné pre pohyb vozidla v teréne).

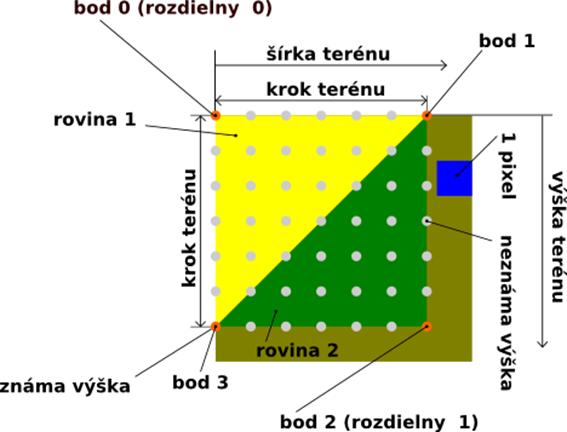
Základná myšlienka pre dopočítanie všetkých neznámych výšok (súradnica Y) celočíselných bodov (Pseudoalgoritmus 17 v prílohe B, obrázok 35) spočíva vo využití rovín (trojuholníkov), ktorými je terén vykresľovaný.

Algoritmus jednoducho zistí v ktorom štvorci v teréne sa nachádza hľadaný bod podľa jeho súradnic X, Z. Následne určí konkrétne, v ktorom trojuholníku. Pre nájdenie správneho trojuholníka sa využíva, že tieto 2 trojuholníky (tvoriace nájdený štvorec) majú 2 nezdieľané body (na obrázku 35 rozdielne). Stačí zistiť, ktorý z týchto rozdielnych bodov je bližšie k nášmu bodu a nájdeme aj hľadaný trojuholník. Potom sa pomocou rovnice roviny (z nájdeného trojuholníka) vypočíta hľadaná výška (súradnica Y) bodu.

Obr. 35 Dopočítanie neexistujúcich výšok terénu

Získanie pyramídy perspektívneho pohľadu

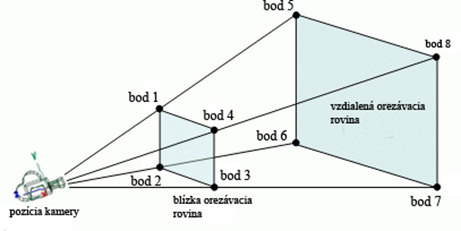
Pod pojmom získanie pyramídy pohľadu si predstavte matematické kroky, ktoré vedú k presnému vymedzeniu pojmu pyramída pohľadu v matematickej podobe. Parametre pyramídy počítame len raz, a to pred spustením renderingu. Týmto krokom dokážeme jednoducho zlepšiť efektivitu renderingu OpenGL aplikácie. Podpriestory terénu, ktoré sa nachádzajú mimo tejto pyramídy sa nevykreslia. Veď načo by sa vykresľovalo niečo, čo nevidieť ? Pyramída pohľadu je v skutočnosti pyramídou s odpíleným vrcholom. Takáto pyramída pozostáva zo 6 rovín, a to z blízkej, vzdialenej, ľavej, pravej, hornej a dolnej. Roviny sú zadefinované tak, že ich normálové vektory smerujú do vnútra pyramídy.

Obr. 36 Znázornenie bodov pyramídy perspektívneho pohľadu

Zadefinujeme (Obrázok 36/37):

  • P=pozíciakamery
  • [math]vyska_1[/math]=výška blízkej orezávacej roviny
  • [math]sirka_1[/math]=šírka blízkej orezávacej roviny
  • [math]vzdialenost_2[/math]=vzdialenosť od kamery ku vzdialenej orezávacej rovine
  • [math]vyska_2[/math]=výška vzdialenej orezávacej roviny
  • [math]sirka_2[/math]=šírka vzdialenej orezávacej roviny
  • d=normalizovaný vektor smeru pozorovania
  • up=normalizovaný normálový vektor hornej plochy kamery
  • vr=normalizovaný vektor smerujúci vpravo

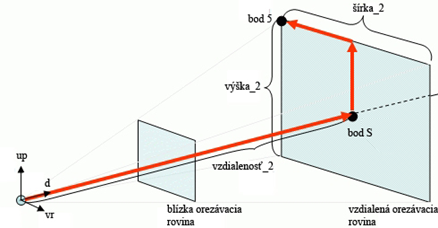
Ak zistíme polohu bodu S(Obrázok 37), ľahko určíme ostatné body. Bod S slúži len ako nástroj na zistenie bodov 5, 6, 7, 8 (Obrázok 36).

Výpočet pre bod S (Obrázok 37):

Obr. 37 Zobrazenie pyramídy perspektívneho pohľadu s vektormi kamery

[math]S=P+d*vzdialenost_2[/math]

Výpočet pre body 5, 6, 7, 8 (Obrázok 36):

[math]bod_5=S+(up*vyska_2/2)–(vr*sirka_2/2)[/math]

[math]bod_6=S-(up*vyska_2/2)–(vr*sirka_2/2)[/math]

[math]bod_7=S-(up*vyska_2/2)–(vr*sirka_2/2)[/math]

[math]bod_8=S+(up*vyska_2/2)–(vr*sirka_2/2)[/math]

Analogicky sa vykoná výpočet pre body 1, 2, 3, 4 (Obrázok 36):

[math]S=P+d*vzdialenost_1[/math]


[math]bod_1=S+(up*vyska_1/2)–(vr*sirka_1/2)[/math]

[math]bod_2=S-(up*vyska_1/2)–(vr*sirka_1/2)[/math]

[math]bod_3=S-(up*vyska_1/2)–(vr*sirka_1/2)[/math]

[math]bod_4=S+(up*vyska_1/2)–(vr*sirka_1/2)[/math]

Blízka orezávacia rovina môže byť definovaná vektorom dako normálou a bodom Xako bodom v tejto rovine. A vektor -d môžeme použiť ako normálu pre vzdialenú orezávaciu rovinu a bod v tejto rovine je bod S. Musíme si uvedomiť, že bod P je výnimočný bod, je to pozícia kamery a zároveň leží aj v ostatných orezávacích rovinách (ľavá, pravá, horná, spodná).

Obr. 38 Postup výpočtu normály pre pravú orezávaciu rovinu

Ukážkový výpočet normály pre pravú orezávaciu rovinu (Obrázok 38): Vypočítame [math]a=d*vzdialenost_1+vr*sirka_1/2[/math], vektor aje v podstate vektorový súčet vektorov [math]d*vzdialenost_1[/math] a vektora [math]vr*sirka_1/2[/math]. Pri tomto vektore nás nezaujíma veľkosť, ale len smer, normalizujeme ho. Naša hľadaná normála je [math]normala_{pravej roviny} =up × a[/math] jednoducho odvodená z definície vektorového súčinu.

Vykresľovanie terénu

Vykresľovanie terénu znamená vykresliť všetky viditeľné podpriestory, ktoré úspešne prešli testom (Pseudoalgoritmus 18, príloha B). Test sa vykoná pre všetky podpriestory. Uskutočňuje sa dosadením každého z 8 bodov (transformovaných aktuálnou MP maticou,[math]bo{{d}_{transf}}=MP*bod[/math]) ohraničenia priestoru do každej zo 6 rovín pyramídy pohľadu. Ak podpriestor leží celý v pyramíde musí mať každý bod podpriestoru kladnú vzdialenosť od každej roviny, pretože jedine vtedy sa nachádza v smere normál rovín, ktoré všetky smerujú dovnútra pyramídy.

Ak priestor leží čiastočne v pyramíde, znamená to, že aspoň jeden bod podpriestoru má kladnú vzdialenosť od každej roviny pyramídy. Toto sú dva prípady kedy musíme podpriestor terénu vykresliť.

Po teste viditeľnosti (Pseudoalgoritmus 18, príloha B) nasleduje cyklus, ktorý podľa výsledku testu vykreslí alebo nevykreslí daný priestor. Vykresľovanie prebieha pomocou polí vrcholov s multitextúrovaním a trianguláciou. Každý riadok terénu začína troma bodmi trojuholníka, a potom pokračuje pridávaním jedného bodu s ohľadom na vinutie polygónu.

Technológia polí vrcholov výrazne urýchľuje aplikáciu, pretože pre takýto spôsob vykresľovania primitív stačí zadať len ukazovateľ na dané pole súradníc bodov a počet prvkov poľa. Vďaka tomu prechádzanie cyklami už nemusí byť uskutočňované pre každý bod poľa, ale len ako prechod na nový riadok kvôli triangulácii.

Kamerový systém Kameru v simulácii „vytváram” volaním funkcie gluLookAt. Funkcia gluLookAt vytvára pozorovateľskú transformáciu vo forme modelovacej matice. Táto matica nám transformuje objekty v scéne do pozorovateľského priestoru. Dôležité parametre kamerového systému, ktoré som zostrojil a programovo implementoval sú smerové vektory [math]vd=[v{{d}_{x}},v{{d}_{y}},v{{d}_{z}}][/math] (smer pozorovania), [math]vu=[v{{u}_{x}},v{{u}_{y}},v{{u}_{z}}][/math](normálový vektor kolmý na hornú plochu kamery), [math]r=[v{{r}_{x}},v{{r}_{y}},v{{r}_{z}}][/math](pravý vektor) a bod [math]vp=[v{{p}_{x}},v{{p}_{y}},v{{p}_{z}}][/math](bod odkiaľ sa pozeráme, poloha kamery).

Funkciu gluLookAt môžeme nahradiť (vysvetliť) aj vlastnou konštrukciou príkazov, pričom musíme poznať [math]vp=[v{{p}_{x}},v{{p}_{y}},v{{p}_{z}}][/math], bod na ktorý sa pozeráme [math]centrum=[v{{p}_{x}}+v{{d}_{x}},v{{p}_{y}}+v{{d}_{y}},v{{p}_{z}}+v{{d}_{z}}][/math] a [math]vu=[v{{u}_{x}},v{{u}_{y}},v{{u}_{z}}][/math], ktorý normalizujeme.

Z týchto parametrov odvodíme jednotkový vektor [math]d=[centru{{m}_{x}}-v{{p}_{x}},centru{{m}_{y}}-v{{p}_{y}},centru{{m}_{z}}-v{{p}_{z}}][/math]. Potom zistíme hodnotu vektora vpravo z vektorového súčinu vr=vd×vu, normalizujeme ho a vypočítame aj nový jednotkový normálový vektor kamery pomocou vu=vr×vd. Zistili sme ako vyzerá aktuálny súradnicový systém kamery. Vytvoríme transformačnú maticu 3x3 (modelovacia transformácia), ktorá je v podstate iverznou maticou k matici súradnicového systému kamery (stačí vytvoriť transponovanú maticu, pretože sa jedná o ortonormálny systém) a s doplnením na homogénnu maticu (4x4) :

[math]F=\begin{matrix} v{{r}_{x}} & v{{r}_{y}} & v{{r}_{z}} & 0 \\ u{{p}_{x}} & u{{p}_{y}} & u{{p}_{z}} & 0 \\ -v{{d}_{x}} & -v{{d}_{y}} & -v{{d}_{z}} & 0 \\ 0 & 0 & 0 & 1 \\ \end{matrix}[/math]

Potrebujeme ešte vytvoriť transformačnú maticu posunu T, ktorá zabezpečí posun (inverzne ku kamere) o opačné hodnoty ako sú súradnice polohy kamery v globálnom súradnicovom systéme, aby bod, na ktorý sa pozeráme bol počiatok. Výsledná modelovacia matica, ktorá reprezentuje pozorovateľskú transformáciu (totožnú s gluLookAt) bude F.T.

Lietajúca kamera

Interakcia pre tento druh kamery je vyriešená pomocou kláves 'W','A', 'S', 'D', 'R', 'E' a pohybov kurzoru myši. Pri interakcii s jednou z kláves 'W', 'A', 'S', 'D' automaticky nastane posunutie v smere niektorej osi kamery (v smere/protismere vr a vd). Deje sa to jednoduchým pričítaním časti vektora vd alebo vr k bodu polohy kamery vp. Časť vektora získame vynásobením jednotkového vektora vd premennou [math]posun_z[/math] alebo vr premennou [math]posun_x[/math]. Veľkosť týchto premenných sa určuje po každom stlačení príslušnej klávesy priradením aktuálnej veľkosti posunu pomocou konštanty [math]velkost_{posunu}[/math].Veľkosť konštanty [math]velkost_{posunu}[/math] zmeníme klávesami 'R', 'E'. Potom pre premenné posunov a pozíciu kamery platí (v danom poradí):


[math]\begin{align} & posu{{n}_{x}}=\pm velkos{{t}_{posunu}} \\ & posu{{n}_{z}}=\pm velkos{{t}_{posunu}} \\ & vp=vp+posu{{n}_{x}}*vr+posu{{n}_{z}}*vd \\ \end{align}[/math]

Po pričítaní ku aktuálnej pozícii kamery sa pozícia kamery vp posunie o nejaký kúsok v smere/protismere vd alebo vr. Podobne funguje aj interakcia s myšou. Zmena smeru pozorovania vd začína výpočtom miery zmeny posunu vzhľadom na polohu kurzoru myši na stred obrazovky, platí :


[math]\begin{align} & mier{{a}_{x}}=(kurzo{{r}_{x}}-sirka\_okna*0.5)*0.005 \\ & mier{{a}_{y}}=(vyska\_okna*0.5-kurzo{{r}_{y}})*0.005 \\ \end{align}[/math]

Pre nový smer pozorovania vd a vektor vpravo vr platí (v danom poradí):

[math]\begin{align} & vr=\frac{vd\times vu}{\left| vd\times vu \right|} \\ & vd=vd+mier{{a}_{y}}*vu+mier{{a}_{x}}*vr \\ & vd=\frac{vd}{vd} \\ \end{align}[/math]

Vzdialenosť k bodu, na ktorý sa pozeráme vd+vpje z bodu pozorovania vp vždy 1, pretože vd je jednotkový vektor. Po každej takejto transformácii treba nastaviť polohu kurzoru myši na stred obrazovky a premenné posunu nulovať:

[math]\begin{align} & kurzo{{r}_{x}}=\check{s}\acute{i}rka\_okna/2 \\ & kurzo{{r}_{y}}=v\acute{y}\check{s}ka\_okna/2 \\ & posu{{n}_{x}}=0 \\ & posu{{n}_{z}}=0 \\ \end{align}[/math]


Prezentačná kamera

Smer pozorovania prezentačnej kamery je vždy smerom do polohy ťažiska vozidla. Kamera automaticky nasleduje vozidlo z premenlivej výšky vypočítanej z polohy kamery v teréne (i mimo terénu). Poloha kamery na osiach X, Z je ľubovoľná. Pred prechodom do režimu prezentačnej kamery môžeme pomocou lietajúcej kamery vybrať ľubovoľnú polohu na osiach X, Z. Najprv vypočítame aktuálny vektor kamery ukazujúci vpravo vr:

  • [math]posun_x[/math]=budúci posun ťažiska na osi X
  • [math]posun_z[/math]=budúci posun ťažiska na osi Z
  • vd=smer pozorovania
  • vu=vektor kolmý na vrchnú plochu kamery
  • vr=vd×vu

Ďalej potrebujeme vyjadriť posun polohy kamery vpv globálnom súradnicovom systéme (GSS) na osiach X, Z a aj polohu bodu pozorovania"bod_pozorovania" (budúce ťažisko vyjadrené v súradnicovom systéme terénu) v GSS:

posun_terénu=[x,y,z], určuje polohu terénu v GSS

  • [math]vp_x=vp_x+posun_x[/math]
  • [math]vp_z=vp_z+posun_z[/math]
  • [math]{bod pozorovania}_{x}={bod pozorovania}_{x}+{posun terénu}_{x}[/math]
  • [math]{bod pozorovania}_{y}={bod pozorovania}_{y}+{posun terénu}_{y}[/math]
  • [math]{bod pozorovania}_{z}={bod pozorovania}_{z}+{posun terénu}_{z}[/math]

Pre správny výpočet výšky kamery v teréne musíme poznať aj polohu kamery v súradnicovom systéme terénu (TSS) vplna osiach X, Z:

  • [math]vpl_x=vp_x- {posun terénu}_{x}[/math]
  • [math]vpl_z=vp_z- {posun terénu}_{z}[/math]

Reálne hodnoty súradníc X, Z (s desatinnou čiarkou) prepočítanej polohy kamery vpl zaokrúhlime k najbližšej celočíselnej hodnote. Ak tieto súradnice X, Z vektora vplurčujú polohu kamery mimo terénu nahradíme ich súradnicami X, Z najbližšieho celočíselneho bodu terénu. Najbližší bod uprednostňujem aj z dôvodu plynulého prechodu kamery z oblasti mimo terénu na terén.

Výsledné celočíselné hodnoty môžeme využiť ako indexy dvojrozmerného poľa prevýšková"_" mapa(výšková mapa), pričom hodnota tohto poľa s týmito indexami (X, Z) predstavuje výšku bodu v teréne na týchto súradniciach X, Z. Potom pre súradnicu Y (výška) polohy kamery vpa výsledný smer pozorovania vdplatí (v danom poradí):

[math]\begin{align} & v{{p}_{y}}=v{{p}_{y}}+vyskova\_mapa[vp{{l}_{z}}][vp{{l}_{x}}]+30 \\ & v{{d}_{x}}=bod\_pozorovani{{a}_{x}}-v{{p}_{x}} \\ & v{{d}_{y}}=bod\_pozorovani{{a}_{y}}-v{{p}_{y}} \\ & v{{d}_{z}}=bod\_pozorovani{{a}_{z}}-v{{p}_{z}} \\ \end{align}[/math]


Kamera za vozidlom

Výpočet začína vyjadrením polohy kamery vpl vzhľadom na ťažisko vozidla "bod_pozorovania" v súradnicovom systéme terénu (TSS), ktoré je zároveň bodom pozorovania tejto kamery (v poradí):

  • polomer_vozidla=určuje užívateľ v konfig.súbore vozidla
  • T=4x4 matica,posun o súradnice X,Z ťažiska vyjadreného v SS terénu
  • R=4x4 matica,rotácia o uhol pootočenia kolies vozidla"
  • [math]vpl_x[/math]=-polomer_vozidla-40
  • [math]vpl_y=0[/math]
  • [math]vpl_z=0[/math]

Nasleduje transformácia maticami:

[math]vpl=T.R.vpl[/math]

Ďalej potrebujeme vyjadriť polohu kamery v globálnom súradnicovom systéme (GSS) ako vpa polohu ťažiska "bod_pozorovania" (vyjadrené v TSS) v GSS:

  • posun_terénu="[x,y,z],určuje polohu terénu v GSS
  • [math]vp_x=vpl_x+{posun terénu}_{x}[/math]
  • [math]vp_y=vpl_y+{posun terénu}_{y}[/math]
  • [math]vp_z=vpl_z+{posun terénu}_{z}[/math]
  • [math]{bod pozorovania}_{x}={bod pozorovania}_{x}+{posun terénu}_{x}[/math]
  • [math]{bod pozorovania}_{y}={bod pozorovania}_{y}+{posun terénu}_{y}[/math]
  • [math]{bod pozorovania}_{z}={bod pozorovania}_{z}+{posun terénu}_{z}[/math]

Reálne hodnoty súradníc X, Z (s desatinnou čiarkou) polohy kamery vplvyjadrenej v TSS zaokrúhlime k najbližšej celočíselnej hodnote. Ak tieto súradnice X, Z vektora vplurčujú polohu kamery mimo terénu nahradíme ich súradnicami X, Z najbližšieho celočíselneho bodu terénu. Najbližší bod upredňostňujem aj z dôvodu plynulého prechodu kamery z oblasti mimo terénu na terén.

Výsledné celočíselné hodnoty môžeme využiť ako indexy dvojrozmerného poľa prevýšková"_" mapa(výšková mapa), pričom hodnota tohto poľa s týmito indexami (X, Z) predstavuje výšku bodu v teréne na týchto súradniciach X, Z. Potom pre súradnicu Y (výška) polohy kamery vpv GSS a výsledný smer pozorovania vd platí (v danom poradí):

[math]\begin{align} & v{{p}_{y}}=v{{p}_{y}}+vyskova\_mapa[vp{{l}_{z}}][vp{{l}_{x}}]+30 \\ & v{{d}_{x}}=bod\_pozorovani{{a}_{x}}-v{{p}_{x}} \\ & v{{d}_{y}}=bod\_pozorovani{{a}_{y}}-v{{p}_{y}} \\ & v{{d}_{z}}=bod\_pozorovani{{a}_{z}}-v{{p}_{z}} \\ \end{align}[/math]

Rotačná kamera

Kroky potrebné k vytvoreniu a fungovaniu rotačnej kamery sú skoro totožné s kamerou za vozidlom. Jediný rozdiel je v spôsobe určovania natočenia polohy kamery vzhľadom na ťažisko vozidla.

Výpočet začína vyjadrením polohy kamery vplvzhľadom na ťažisko vozidla "bod_pozorovania" v súradnicovom systéme terénu (TSS), ktoré je zároveň bodom pozorovania tejto kamery (v nasledujúcom poradí):

  • polomer_vozidla=určuje užívateľ v konfig.súbore vozidla
  • T=4x4 matica,posun o súradnice X,Z ťažiska vyjadreného v SS terénu
  • R=4x4 matica,rotácia o uhol rotačný_uhol

[math]\begin{align} & IF(++rotacny\_uhol\equiv 360{}^\circ ) \\ & \ \ \ \ rota\check{c}n\acute{y}\_uhol\leftarrow 1{}^\circ \\ & vp{{l}_{x}}=-polomer\_vozidla-60 \\ & vp{{l}_{y}}=0 \\ & vp{{l}_{z}}=0 \\ \end{align}[/math]

Nasleduje transformácia maticami:

[math]vpl=T.R.vpl[/math]

Ďalej potrebujeme vyjadriť polohu kamery v globálnom súradnicovom systéme (GSS) ako vpa polohu ťažiska "bod_pozorovania" taktiež v GSS:

[math]\begin{align} & posun\_terenu=[x,y,z]\text{, }\!\!~\!\!\text{ urcuje }\!\!~\!\!\text{ polohu }\!\!~\!\!\text{ terenu }\!\!~\!\!\text{ v }\!\!~\!\!\text{ GSS} \\ & v{{p}_{x}}=vp{{l}_{x}}+posun\_teren{{u}_{x}} \\ & v{{p}_{y}}=vp{{l}_{y}}+posun\_teren{{u}_{y}} \\ & v{{p}_{z}}=vp{{l}_{z}}+posun\_teren{{u}_{z}} \\ & bod\_pozorovani{{a}_{x}}=bod\_pozorovani{{a}_{x}}+posun\_teren{{u}_{x}} \\ & bod\_pozorovani{{a}_{y}}=bod\_pozorovani{{a}_{y}}+posun\_teren{{u}_{x}} \\ & bod\_pozorovani{{a}_{z}}=bod\_pozorovani{{a}_{z}}+posun\_teren{{u}_{x}} \\ \end{align}[/math]

Reálne hodnoty súradníc X, Z (s desatinnou čiarkou) polohy kamery vpl vyjadrenej v TSS zaokrúhlime k najbližšej celočíselnej hodnote. Ak tieto súradnice X, Z vektora vplurčujú polohu kamery mimo terénu nahradíme ich súradnicami X, Z najbližšieho celočíselneho bodu terénu. Najbližší bod upredňostňujem aj z dôvodu plynulého prechodu kamery z oblasti mimo terénu na terén.

Výsledné celočíselné hodnoty môžeme využiť ako indexy dvojrozmerného poľa pre výšková_mapa (výšková mapa), pričom hodnota tohto poľa s týmito indexami (X, Z) predstavuje výšku bodu v teréne na týchto súradniciach X, Z. Potom pre súradnicu Y (výška) polohy kamery vpv GSS a výsledný smer pozorovania vdplatí (v danom poradí):

[math]\begin{align} & v{{p}_{y}}=v{{p}_{y}}+vyskova\_mapa[vp{{l}_{z}}][vp{{l}_{x}}]+30 \\ & v{{d}_{x}}=bod\_pozorovani{{a}_{x}}-v{{p}_{x}} \\ & v{{d}_{y}}=bod\_pozorovani{{a}_{y}}-v{{p}_{y}} \\ & v{{d}_{z}}=bod\_pozorovani{{a}_{z}}-v{{p}_{z}} \\ \end{align}[/math]

Záver

Úlohou tejto práce bolo vytvoriť multi-platformné simulačné prostredie pre pohyb vozidla v závislosti od užívateľských parametrov. Náročnosť témy ma donútila venovať sa štúdiu rôznych oblastí potrebných pre teoretické základy k praktickej realizácii. Boli to predovšetkým matematika, počítačová grafika, umelá inteligencia, knižnice v jazyku C++, pokročilé možnosti programovania v C++ a spôsoby implementácie modulov jazyka Python v C++. Z tohto dôvodu som rozdelil diplomovú prácu na dve hlavné časti, teoretickú a praktickú. Významné miesto v prvej časti zaberá knižnica OpenGL, SDL, Libconfig a inkrementálno-heuristický algoritmus D* Lite.

V praktickej časti som sa zaoberal predovšetkým vlastnými návrhmi algoritmov a iných riešení, ich implementáciami a vlastnou implementáciou i úpravami finálnej verzie algoritmu D* Lite. Vytvoril som vlastný konfiguračný a parsovací systém pre konštrukciu užívateľského menu. Užívateľ podľa jasných pravidiel (opísaných v práci) dokáže skonštruovať ľubovoľné, vlastné obrázkové menu priamo zápisom do konfiguračného súboru. Existujúce menu s vyplneným konfiguračným súborom predstavuje vstupnú bránu k simulácii, slúži na zmenu parametrov vykresľovania, zmenu hudobnej zložky a vstup do simulácie. Pre tvorbu grafických dát do menu som využil pokročilé vlastnosti programu Photoshop CS3.

Užívateľské parametre zapísané do konfiguračného súboru vozidla sú základom pre vytvorenie vozidla s rôznymi proporciami. Vozidlo je ovládané priamou interakciou s užívateľom alebo algoritmom D* Lite. Pri priamej interakcii užívateľ prostredníctvom klávesnice naviguje vozidlo nejakým smerom. Pri nepriamej interakcii riadiaci algoritmus naviguje vozidlo k cieľu, určeného z modulu jazyka Python.

Asi najdôležitejšou časťou celej aplikácie je algoritmus zabezpečujúci interakciu medzi vozidlom a riadiacim algoritmom. Algoritmus prijíma vždy nový bod (budúcu polohu vozidla), vypočítaný riadiacim algoritmom. Následne rozpozná výhodnejší smer pohybu (vektor pohybu vzad / vpred). Ak je tento najvýhodnejší smer totožný so smerom do bodu, tak sa vykoná posun v danom smere (v závislosti na FPS), ak nie tak algoritmus musí vybrať najvýhodnejšiu operáciu (odčítať / pripočítať uhol), aby sa vozidlo natočilo na správny smer, a potom nastane posun. Ak sa dosiahne ponúknutý bod, vyžiadava sa vždy nový najvýhodnejší, až pokým vozidlo nedosiahne cieľ.

Zostavil som aj súbor algoritmov, ktoré dovoľujú užívateľovi definovať parametre aproximačnej mapy na základe aproximačného polomeru. Riadiaci algoritmus D* Lite potom pracuje predovšetkým s takouto mapou, čo má za následok plynulejší prechod terénom a menšie nároky na procesor a pamäť. Nevyhnutnú súčasť simulačného prostredia predstavuje terén, ktorý je parametrizovaný priamo zo svojho konfiguračného súboru užívateľom alebo aplikáciou na základe parametrov pre algoritmus D* Lite. Užívateľ nastavuje napríklad počet šírkových a výškových podpriestorov (z ktorých vynásobením získame celkový počet podpriestorov), krok terénu (koľký bod v poradí bude načítavaný z výškovej mapy) a Chebyshevov polomer pre počet susedov (určuje maximálny možný počet susedov pre aproximáciu bodu mapy).

Vymyslel som algoritmus (súbor 4 algoritmov), ktorý sa snaží rovnomerne rozložiť body terénu do podpriestorov aj na základe kroku terénu. Plynulú výšku v teréne vytváram aproximáciou so susedmi bodu do vzdialenosti určenej užívateľom. Na dopočítanie výšok neexistujúcich bodov som definoval algoritmus, ktorý ich vyráta z roviny (trojuholníka existujúcich 3 bodov podľa kroku), v ktorom leží. Výsledok práce v režime pohybu vozidla prezentujem pomocou piatich kamerových systémov (v režime bez vozidla je k dispozícii len 1), ktoré sú interaktívne a k dispozícii užívateľovi po celú dobu simulácie v režime s vozidlom.

Z programátorskeho hľadiska (pozri UML diagramy v prílohe D) bola táto téma tvrdým orieškom z dôvodu obrovského rozsahu a náročnosti. Snažil som sa vytvoriť systém podobný stromovému grafu, kde vyššie postavený prvok vo vetve posiela „globálne” (globálne len v rámci tejto skupiny tried) zdieľané dáta nižšie postavenému členovi.

Na vrchole celej aplikácie sa nachádza trieda, ktorá jediná vie ako správne nastaviť a skonštruovať tieto dáta. Jediná má správny kľúč, ktorý použije ako parameter do šablóny triedy, ktorá je dedičom dátovej triedy (existuje špecializácia takejto šablóny so správnym kľúčom). Ak by sa použil hocijaký iný kľúč systém by skončil vyhodením výnimky (pre takýto prípad neexistuje špecializácia šablóny).

Posielanie dátovej triedy („globálne“ dáta) prebieha na základe pretypovania na rodiča (upcasting), aby sa neodhalil kľúč pre ostatné triedy v hierarchii. Vytvoril som triedu pre odchytávanie výnimiek aj triedu na logovanie, ktorá informuje užívateľa predovšetkým o chybách a upozorneniach systému. Niektoré kritické časti kódu som kvôli zvýšeniu rýchlosti preprogramoval pomocou metaprogramovania. To znamená, že výsledky sa tvoria už v čase kompilácie a aplikácia nie je zaťažovaná počas behu.

Veľký počet tried som zabezpečil tak, aby boli jednoinštančné, a to rekurzívnym dedením zo špeciálnej šablóny, ktorej parametrom je uvažovaná trieda. Rozvoj aplikácie môže prebiehať vo všetkých oblastiach. Ďalším krokom by mohlo byť napríklad vytvorenie multiagentového systému, pridanie možnosti tvoriť prekážky v teréne, aplikovanie fyzikálnych zákonov na vozidlo, zbavenie sa textových konfiguračných súborov a ich vloženie do systému menu, zrýchlenie aplikácie, zvýšenie parametrizácie kódu ďalšími šablónami, ošetrenie všetkých chybových situácií atď.

Zoznam použitej literatúry

  1. ŽÁRA J. - BENEŠ B. - SOCHOR J. - FELKEL P. : Moderní počítačová grafika (2. vydání), Computer Press, 2005, ISBN 80-251-0454-0
  2. WRIGHT R., Jr. - LIPCHAK B. - HAEMEL N. : OpenGL Superbible Fourth Edition, Addison-Wesley, 2007, ISBN 0-321-49882-8
  3. ASTLE D. - HAWKINS K. : Beginning OpenGL Game Programming, Premier Press, 2004, ISBN 1-59200-369-9
  4. SEDDON C. : OpenGL Game Development, Worldware Publishing, 2005, ISBN 1-55622-989-5
  5. McREYNOLDS T. - B L Y T H E D. : Advanced Graphics Programming using OpenGL, Morgan Kaufmann Publishers, 2005, ISBN 1-55860-659-9
  6. MARTZ P.: OpenGL Distilled, Addison Wesley Proffesional, 2006, ISBN 0-321-33679-8
  7. POLACK T. : Focus on 3d terrain programming, Premier Press, 2003, ISBN: 1-59200-028-2
  8. OpenGL tutorial http://www.videotutorialsrock.com [1. 3. 2010]
  9. The Official Guide to Learning OpenGL, Version 1.1. http://www.glprogramming.com/red/ [1. 3. 2010]
  10. Seriál SDL: Hry nejen pro Linux http://www.root.cz/serialy/sdl-hry-nejen-pro-linux/ [1. 3. 2010]
  11. View Frustum Culling Tutorial http://www.lighthouse3d.com/opengl/viewfrustum/ [1. 1. 2009]
  12. A Library For Processing Structured Configuration Files, Version 1.4.4 http://www.hyperrealm.com/libconfig/libconfig_manual.html [1. 6. 2009]
  13. Python (programovací jazyk) http://sk.wikipedia.org/wiki/Python_(programovací_jazyk) [1. 6. 2009]
  14. Extending and Embedding the Python Interpreter http://docs.python.org/release/2.5.2/ext/ext.html [1. 4. 2010]
  15. Chapter 1. python 1.0 http://www.boost.org/doc/libs/1_42_0/libs/python/doc/tutorial/doc/html/index [9. 10. 2009]
  16. Path Planning with D*Lite http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.67.6521 [1. 6. 2009]
  17. FPS: Konstantní rychlost animace http://nehe.ceske-hry.cz/cl_fps.php [6. 6. 2009]
Zdroj: „http://www.kiwiki.info/index.php?title=Multi-analýza_a_syntéza_simulačného_programu&oldid=6847“