Nekooperatívna teória: Rozdiel medzi revíziami
| Riadok 28: | Riadok 28: | ||
(Prvú úlohu si označíme ako stratégia(U1, V1), druhú úlohu ako stratégia(U2, V2), a kombináciu úloh ako stratégiu(U3, V3).) | (Prvú úlohu si označíme ako stratégia(U1, V1), druhú úlohu ako stratégia(U2, V2), a kombináciu úloh ako stratégiu(U3, V3).) | ||
| − | < | + | |
| + | [[Súbor:NE.jpg]] | ||
| + | |||
| + | ''Riešenie:'' | ||
| + | |||
| + | Nashove ekvilibriá hľadáme tak, že v riadkoch hľadáme maximum z výplat Hráča2, a v stĺpcoch maximum z výplat Hráča1. | ||
| + | |||
| + | <math>a1=maxvJ1(u,v)</math> | ||
| + | |||
| + | <math>a2=maxJ2(u,v)</math> | ||
| + | |||
| + | Potom hľadáme bunku, v ktorej sa nachádzajú obidve maximá. | ||
| + | |||
| + | <math> (a1,a2)=(Ju,Jv) </math> | ||
| + | |||
| + | [[Súbor:NE1.jpg]] | ||
==Dominantné stratégie== | ==Dominantné stratégie== | ||
Verzia zo dňa a času 18:59, 2. február 2010
| 1. | Neantagonistický konflikt dvoch hráčov |
| 2. | Nekooperatívna teória |
| 3. | Kooperatívna teória - prenosová výhra |
| 4. | Kooperatívna teória - neprenosová výhra
|
Obsah
Nekooperatívna Teória
Jedná sa o bimaticovú hru, pričom postup, akým hráč vyberá svoje stratégie je principiálne podobný ako pri maticových hrách. Každý hráč hodnotí svoje stratégie podľa toho, akými stratégiami by odpovedal druhý hráč. Predpokladaná odpoveď druhého hráča je daná jeho výplatnými funkciami, veľkosťou jeho výplat, ktoré chce každý hráč maximalizovať. Z týchto odpovedí si hráči vyberú takú stratégiu, ktorá by priniesla ten najlepší možný výsledok, to znamená, pri ktorom by všetci hráči dosiahli svoje najlepšie výsledky. Pretože však neplatí vzťah nulového súčtu výhry a prehry, je stupeň vynútenej voľby stratégii slabší. Pokiaľ hráč urobí chybu, zvolí inú než rovnovážnu stratégiu, nemusí byť druhý hráč zvýhodnený.
Nashove ekvilibrum
Celú situáciu komplikuje aj to, že nekooperatívna bimaticová hra, môže mať rôzny počet Nashových (rovnovážnych) bodov:
- -Jeden Nashov bod
- -Niekoľko Nashových bodov
- -Žiadny Nashov bod
Nashov rovnovážny bod(ekvilibrium) je vlastne bod, v ktorom nastane rovnováha najlepších možných výsledkov, inak povedané je to dvojica bodov, v ktorých majú obaja protihráči svoju najlepšiu stratégiu. Množinu Nashových ekvilibrií označujeme: [math]NE=[(A1,B3);(C3,B2)][/math]
Príklad1:
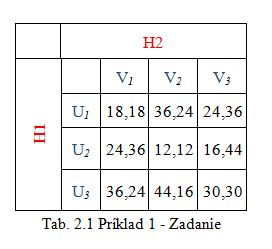
Janko(H1) a Jožko(H2) sú konkurenti, ktorý dostali dve úlohy. Môžu si ich rozdeliť, každý bude riešiť jednu(aj rovnakú) úlohu, alebo sa môžu rozhodnúť pre riešenie oboch úloh(teda aspoň čiastočnú spoluprácu). Odmena za prvú úlohu je 36eur, za druhú úlohu je 24eur. Pokiaľ budú spolupracovať na pol, odmenu si tiež rozdelia na pol. Pokiaľ sa jeden z nich bude jednej úlohe venovať sám, a na druhej úlohe bude spolupracovať, môže sa druhej úlohe venovať len z jednej tretiny, a tiež si tak rozdelia odmenu za túto úlohu. Samostatné riešenie samozrejme znamená zisk celej odmeny. Obaja sa rozhodujú, ako úlohu vyriešiť, pritom každý chce získať väčšiu odmenu ako druhý.
(Prvú úlohu si označíme ako stratégia(U1, V1), druhú úlohu ako stratégia(U2, V2), a kombináciu úloh ako stratégiu(U3, V3).)
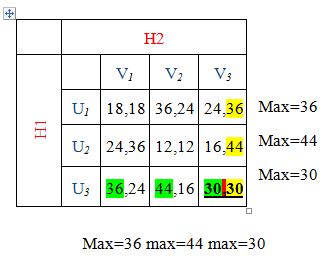
Riešenie:
Nashove ekvilibriá hľadáme tak, že v riadkoch hľadáme maximum z výplat Hráča2, a v stĺpcoch maximum z výplat Hráča1.
[math]a1=maxvJ1(u,v)[/math]
[math]a2=maxJ2(u,v)[/math]
Potom hľadáme bunku, v ktorej sa nachádzajú obidve maximá.
[math] (a1,a2)=(Ju,Jv) [/math]