Triangulacná metóda merania vzdialenosti
| 1. | Prehlad métod merania vzdialenosti |
| 2. | Triangulacná metóda merania vzdialenosti |
| 3. | Návrh a realizácia fotoelektrického parkovacieho senzora
|
Pre riešenie našej problematiky sme si zvolili senzor využívajúci princíp triangulačnej metódy merania vzdialenosti. V tejto kapitole rozoberiem princíp zvolenej metódy pre meranie vzdialenosti optickými snímačmi.
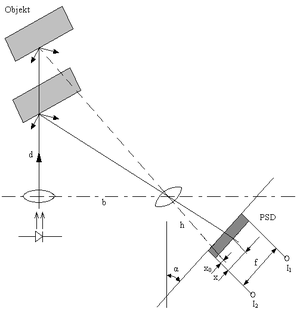
Merací signál sa dá spracovať polohovo citlivým polovodičovým prvkom PSD. Svetelný lúč, ktorý na tento prvok dopadá, vyvolá prúd fotónov, ktorý sa vetví k obom koncom polovodičovej doštičky. Pri rovnakej záťaži na oboch koncoch sa z pomeru oboch prúdov dá určiť poloha svetelnej stopy. Takéto chovanie činí prvok PSD ideálny pre optickú trianguláciu.
Ak sa zvolí α = 90º a x = 0, čo je vlastne tesné umiestnenie optiky v senzore, potom pre toto usporiadanie platí:
|
[math]d=h\cdot b\cdot \frac{1}{x}[/math] |
(2.1) |
S prvkom PSD ďalej dostaneme:
|
[math]d=\frac{h.b}{f}\cdot \frac{\mathop{I}_{1}+\mathop{I}_{2}}{\mathop{I}_{1}}[/math] |
(2.2) |
Vzdialenosť d sa tak dá zistiť meraním prúdov. Vyhodnotenie je možné buď analógovou deličkou alebo mikrokontrolerom s A/D prevodníkom. Dôležitým faktorom je nevýhoda, ktorá nastáva pri meraní difúznym svetlom. Intenzita prijatého svetla klesá so vzdialenosťou a podľa uvedenej rovnice je vzdialenosť nepriamo úmerná prúdu I1. Z toho vyplýva že meraná veličina je nepriamo úmerná tretej mocnine prúdu I1. Jedna z možností minimalizovať tento nedostatok je regulácia vysielaného výkonu, ktorá sa zrealizuje operačným zosilňovačom.
Aj pri použití doregulovania pri emitovaní červeného svetla dochádza k zhoršeniu rozlišovacej schopnosti pre zelené, modré a čierne objekty asi 4-krát. Nežiadúce vplyvy zmiernime tak, že senzor nevystavíme rušivým svetelným vplyvom, nesnímame zrkadliace, priehľadné a porézne predmety. Pri takýchto prípadoch je výhodnejšie použiť obyčajnú LED namiesto laseru, ako zdroj žiarenia [1].
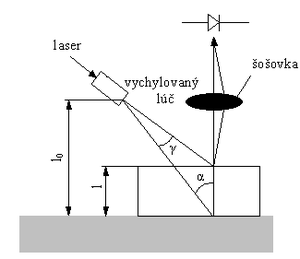
Signál ktorý je nameraný na fotodióde slúži k určeniu časového intervalu medzi okamihom odrazu lúča od základnej roviny a od povrchu predmetu vzdialeného o dĺžku l. Meranie uhla γ je tak nahradené meraním časového intervalu, za ktorý sa pri známej rýchlosti lúča zistí fotodiódou odraz od spodnej a hornej plochy objektu. Z usporiadania dostaneme vzťah pre určenie polohy l:
[math]\frac{l}{\mathop{l}_{0}}=\frac{\sin \gamma }{\sin (\alpha +\gamma )}\cdot \frac{1}{\sin \alpha }[/math]
Pre našu aplikáciu je lepšie využiť triangulačnú metódu bez vychyľovania lúča. Nakoľko je potrebné brať do úvahy problémy s konštrukciou a so samotným vychyľovaním lúča a z toho vyplýva že triangulačná metóda bez vychyľovania lúča je pre nás dostupnejšia [5].